pulp 文档

1 介绍

pulp 是一个用 python 编写的 LP 建模器。

1.1 优化过程

解决优化问题不是一个线性过程，但该过程可以分为五个一般步骤：

• 获取问题描述
• 建立数学模型
• 求解数学模型
• 执行一些优化后分析
• 提出解决方案和分析

然而，在这个过程中经常存在“反馈循环”。例如，在制定和解决优化问题后，您通常需要考虑解决方案的有效性（通常咨询提供问题描述的人）。如果您的解决方案无效，您可能需要更改或更新您的公式，以纳入您对实际问题的新理解。此过程显示在运筹学方法图中。

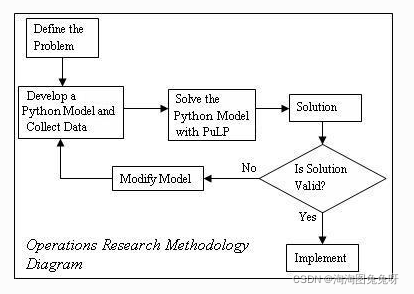
建模过程从定义明确的模型描述开始，然后使用数学来制定数学程序。接下来，建模者将数学程序输入到一些求解器软件中，例如Excel，并对模型进行求解。最后，根据原始模型描述将解决方案转化为决策。

使用 Python 为您提供了一个通过建模过程的“捷径”。通过在 Python 中制定数学程序，您已经将其转换成一种形式，PuLP 建模器可以轻松使用它来调用许多求解器，例如 CPLEX、COIN、gurobi，因此您无需将数学程序输入到求解器软件中. 但是，您通常不会在公式中添加任何“硬”数字，而是使用数据文件“填充”模型，因此创建适当的数据文件需要做一些工作。使用数据文件的好处是同一个模型可以多次使用不同的数据集。

1.1.1 建模过程

模过程是优化过程的“整洁”简化。让我们更详细地考虑优化过程的五个步骤：

1.1.1.1 获取问题描述

这一步的目的是提出一个正式的、严谨的模型描述。通常，您会从对问题的抽象描述和一些数据开始优化项目。通常，您需要花一些时间与提供问题的人（通常称为客户）交谈。通过与客户交谈并考虑可用数据，您可以提出您习惯的更严格的模型描述。有时并非所有数据都是相关的，或者您需要询问客户是否可以提供其他数据。有时，可用数据的限制可能会显著改变您的模型描述和后续公式。

1.1.1.2 建立数学模型

在这一步中，我们从问题描述中识别出关键的可量化决策、限制和目标，并在数学模型中捕捉它们的相互依赖性。我们可以将建模过程分为 4 个关键步骤：

• 确定决策变量。（注意单位）
• 使用决策变量制定目标函数，我们可以构造一个最小化或最大化的目标函数。
• 指定约束条件。（约束条件用决策变量表示）
• 确定目标函数和约束所需的数据。（为了求解您的数学模型，您需要在目标函数或约束中使用一些“硬数字”作为变量边界或变量系数。）

1.1.1.3 求解数学模型

对于相对简单或容易理解的问题，数学模型通常可以求解到最优（即，确定最佳可能的解决方案）。这是使用修正单纯形法或内点法等算法完成的。然而，使用这些技术解决许多工业问题需要很长时间才能达到最优，因此使用不能保证最优的启发式方法来解决。

1.1.1.4 执行一些优化后分析

问题描述中通常存在不确定性（无论是所提供数据的准确性，还是未来数据的价值）。在这种情况下，我们的解决方案的稳健性可以通过执行后优化分析来检查。这涉及确定最佳解决方案在参数的各种变化下将如何变化（例如，给定成本增加或特定机器故障会产生什么影响？）。这种分析对于制定战术或战略决策也很有用（例如，如果我们投资开设另一家工厂，这会对我们的收入产生什么影响？）。

此步骤（以及下一步）中的另一个重要考虑因素是验证数学模型的结果。您应该仔细考虑解决方案的变量值在原始问题描述方面的含义。确保它们对您，更重要的是对您的客户有意义（这就是为什么下一步，提出解决方案和分析很重要）。

1.1.1.5 提出解决方案和分析

优化过程中的一个关键步骤是解决方案的呈现和任何优化后的分析。从数学模型的结果转换回简明易懂的总结与从问题描述到数学模型的转换同样重要。通过优化产生的关键结果和决策必须以易于理解的方式呈现给客户或项目利益相关者。

这一步也是您在未来提出其他工作的基础。这可能包括：

• 定期监控您的数学模型的有效性；
• 进一步分析您的解决方案，为您的客户寻找其他好处；
• 识别未来的优化机会。

1.2 优化概念

1.2.1 线性规划

最简单的数学模型类型是线性模型。要使您的数学模型成为线性模型，您需要满足以下条件：

• 决策变量必须是实变量；
• 目标函数必须是线性表达式；
• 约束条件必须是线性表达式。

线性表达式是如下形式的表达式：

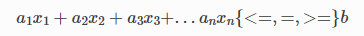
其中，$ai$ 和 b 是已知的常量，$xi$ 是变量。
线性规划是通过修正单纯形法（也称为原始单纯形法）、对偶单纯形法或内点法完成的。

1.2.2 整数规划

整数程序可以使用分支定界过程来求解。

注意对于任何合理大小的 MIP，求解时间随着整数变量数量的增加呈指数增长。

2 案例学习

2.1 混合问题

2.1.1 问题描述

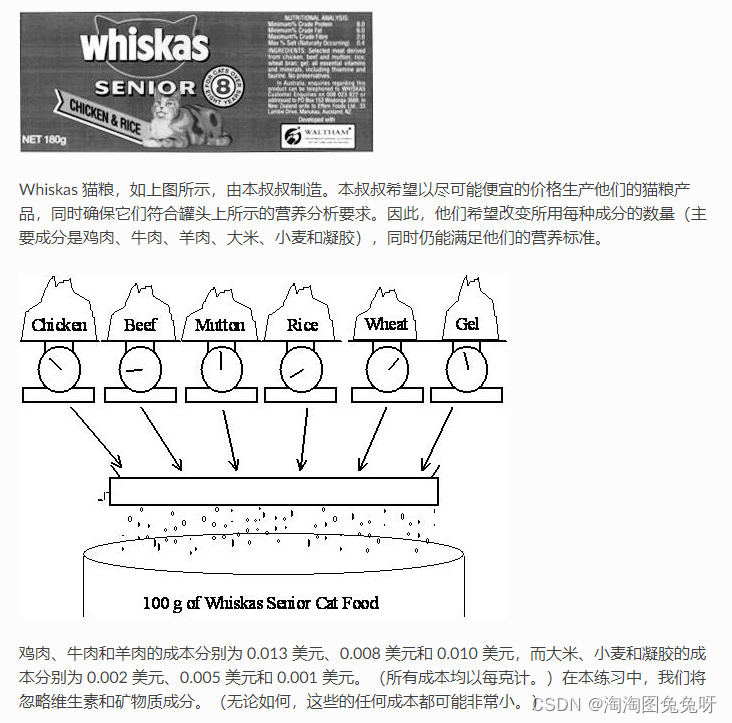
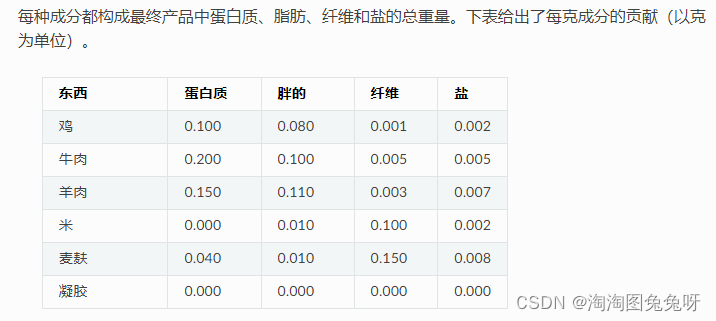
2.1.1.1 问题抽象

一、识别决策变量
假设 Whiskas 想要只用两种原料制作他们的猫粮：鸡肉和牛肉。我们将首先定义我们的决策变量：

二、制定目标函数
目标函数变为：

三、约束条件
对变量的约束是它们的总和必须为 100 并且满足营养需求：

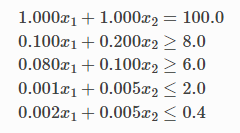
2.1.1.2 简化问题的解决方案

import pulp

x1 = pulp.LpVariable("x1", lowBound=0)
x2 = pulp.LpVariable("x2", lowBound=0)

problem = pulp.LpProblem("The Whiskas Problem", pulp.LpMinimize)
problem += 0.013*x1 + 0.008*x2
problem += x1 + x2 == 100
problem += 0.1*x1 + 0.2*x2 >= 8
problem += 0.08*x1 + 0.1*x2 >= 6
problem += 0.001*x1 + 0.005*x2 <= 2
problem += 0.002*x1 + 0.005*x2 <= 0.4

problem.writeLP("WhiskasModel.lp")
problem.solve()

运行这个文件应该会产生输出，显示鸡肉占 33.33%，牛肉占 66.67%，每罐配料的总成本为 96 美分。

2.1.2 完整问题的解决方案

"""
The Full Whiskas Model Python Formulation for the PuLP Modeller

"""

# Import PuLP modeler functions
from pulp import *

# 创建一个成分列表
Ingredients = ['CHICKEN', 'BEEF', 'MUTTON', 'RICE', 'WHEAT', 'GEL']

# 创建一个关于每种成分的成本的字典
costs = {'CHICKEN': 0.013, 
         'BEEF': 0.008, 
         'MUTTON': 0.010, 
         'RICE': 0.002, 
         'WHEAT': 0.005, 
         'GEL': 0.001}

# 创建一个每种成分中的蛋白质含量的字典
proteinPercent = {'CHICKEN': 0.100, 
                  'BEEF': 0.200, 
                  'MUTTON': 0.150, 
                  'RICE': 0.000, 
                  'WHEAT': 0.040, 
                  'GEL': 0.000}

# 创建一个每种成分中的脂肪含量的字典
fatPercent = {'CHICKEN': 0.080, 
              'BEEF': 0.100, 
              'MUTTON': 0.110, 
              'RICE': 0.010, 
              'WHEAT': 0.010, 
              'GEL': 0.000}

# 创建一个每种成分中的纤维含量的字典
fibrePercent = {'CHICKEN': 0.001, 
                'BEEF': 0.005, 
                'MUTTON': 0.003, 
                'RICE': 0.100, 
                'WHEAT': 0.150, 
                'GEL': 0.000}

# 创建一个每种成分中的盐含量的字典
saltPercent = {'CHICKEN': 0.002, 
               'BEEF': 0.005, 
               'MUTTON': 0.007, 
               'RICE': 0.002, 
               'WHEAT': 0.008, 
               'GEL': 0.000}

# Create the 'prob' variable to contain the problem data
prob = LpProblem("The Whiskas Problem", LpMinimize)

# A dictionary called 'ingredient_vars' is created to contain the referenced Variables
ingredient_vars = LpVariable.dicts("Ingr",Ingredients,0)

# The objective function is added to 'prob' first
prob += lpSum([costs[i]*ingredient_vars[i] for i in Ingredients]), "Total Cost of Ingredients per can"

# The five constraints are added to 'prob'
prob += lpSum([ingredient_vars[i] for i in Ingredients]) == 100, "PercentagesSum"
prob += lpSum([proteinPercent[i] * ingredient_vars[i] for i in Ingredients]) >= 8.0, "ProteinRequirement"
prob += lpSum([fatPercent[i] * ingredient_vars[i] for i in Ingredients]) >= 6.0, "FatRequirement"
prob += lpSum([fibrePercent[i] * ingredient_vars[i] for i in Ingredients]) <= 2.0, "FibreRequirement"
prob += lpSum([saltPercent[i] * ingredient_vars[i] for i in Ingredients]) <= 0.4, "SaltRequirement"

# The problem data is written to an .lp file
prob.writeLP("WhiskasModel2.lp")

# The problem is solved using PuLP's choice of Solver
prob.solve()

# The status of the solution is printed to the screen
print("Status:", LpStatus[prob.status])

# Each of the variables is printed with it's resolved optimum value
for v in prob.variables():
    print(v.name, "=", v.varValue)

# The optimised objective function value is printed to the screen    
print("Total Cost of Ingredients per can = ", value(prob.objective))

最佳解决方案是 60% 牛肉和 40% 凝胶，导致目标函数值为每罐 52 美分。

2.2 以 LP 形式表述的数独问题