从同余到费马小定理再到公钥加密系统——从密码学视角看九省联考压轴题

       听说今年九省联考出了一道十分新颖的压轴题，这勾起了我当年八省联考的回忆，恰好这题的背景颇有密码学的意味，故作此文。

先读题，这题涉及了素数、同余等诸多数论名词，并引入了较少见的“离散对数”并要求考生理解与做一些应用。与基于泰勒展开、琴生不等式等的导数压轴题，基于仿射、极点极线等的解析几何压轴题相同，本题也有其高观点：费马小定理。

       网络上有人把题目中的一些记号转化成了大家更熟悉的常用符号，这个会更清楚一些。

      

       要解释清楚这些，我们需要从头开始，多头呢？从认识数字讲起。

引入

       掰掰自己的手指头，左手伸出来1个手指，右手伸出来1个手指，一共几个手指头呢，我们一般约定俗成地说有2个手指——数一下就知道了。如果一个手指对应一个苹果，那我们就可以算出苹果的数量。

       可惜手指一般一共只有十个，但是苹果却可以有很多个，所以我们发明了代替手指的计数方式——数字，更准确地说是自然数。

       就像手指可以屈伸，数字也可以进行操作，这些操作与数字便构成了自然数的代数系统。

小学时我们就学过四则运算——加减乘除。后来我们又知道了加减互为逆运算，乘除互为逆运算。逆运算总是更复杂，减法引入了负数，除法引入了小数。当然我们还知道更后面的故事：开根引入了虚数，以及一系列不可积的函数也证明了这一点。但是我们解决了，不是吗？

只有一种解决办法吗？当然不是。我们都喜欢整数，至少毕达哥拉斯很喜欢。当我们出于某种目的希望构建一个只有整数的理想国的时候，四则运算是否还可以继续存在？当然可以——需要对除法进行一定的修改——带模除法。

同余

       在解释带模除法除法之前，有必要说说带余除法。

       这就是带余除法。但是这种表示方法有一个弊端。考虑另一个式子：

       根据等号的传递性，所以我们要接受：

       这是荒谬的。但是哪里出错了呢？等号的问题，这里的等号不具有传递性——带余除法的等号两边不全是数字。所以带余除法的数学性质较差，不利于与其他数学结构交互。

       我们有更好的东西——带模除法。

       这个式子表示 a除以p的余数与b除以p的余数相等，也就是a与b除以p的余数相同，也就是同余，这个式子被称为同余式。

所以我们可以发现带模除法不关心商，只关心余数。让我们讨论一下带模除法的性质

首先我们有

这是在说a-b除以p的余数与0除以p的余数相等，就是说a-b除以p的余数是0，就是说a-b整除于p。这条性质是容易证明的。

这像极了两边同时减b。所以自然地我们会问：两边同时减同一个常数可以吗？当然可以。

这是在说a-k除以p的余数与b-k除以p的余数相等，其中k是常数。当然是这样的，有两堆苹果，分成了若干组数量一样的组，各自剩下了数量相等的苹果不能组成一组，现在我从这两堆苹果中拿走数量一样的一些苹果，剩下了的那些苹果的数量当然是一样的。

更进一步，如果这两堆苹果我还拿走了数量不一定相等的几组呢？当然剩下了的那些苹果的数量还是一样的。

所以，这是说a-k-s*p除以p的余数与b-k-t*p除以p的余数相等，其中k、s、t是常数，a-k-s*p=a-（k+s*p），这后面的东西似曾相识。

显然有

所以，这后面减的东西本身就是关于p同余的！整理一下我们有
 

       把c替换成-c，d替换成-d，我们有：
 

用我自己的话说，每一种带模除法都产生了一个关于模的系统，在这个系统中只要遵守模的规则，就依然相安无事，岁月静好。因为a与b同余于p，c与d同余于p，它们四个就是“一家人”，所以它们之间进行运算是可以的。

篇幅所限，我们不加说明地给出带模除法关于乘法的运算律。（因为他们是“一家人”，这是自然的）
 

基于此性质，我们有

这里的指数运算是经典的指数运算。

但是请注意，这个“一家人”的感性想法不适用于经典除法，但是在这里经典除法已经被带模除法代替了，所以经典除法的运算律相对复杂：

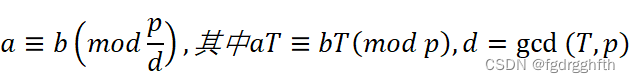
再补充几个带模除法的基本性质

至此我们可以解决第一小题：

求a^(p-1) mod p就是在问a^(p-1) 除以p的余数是多少，代入计算即得，即求1024/11的余数是多少，答案为1。

费马小定理

       首先我们证明费马小定理。设正整数a不整除于某质数p。

       我们考察如下数列：

       此数列模p所得结果互不相同。证明如下：

       即：

       即：

       因为a不整除于p，所以a的质因数分解中不包含p。

       因为x,y∈[1,p-1]，所以x-y∈[0,p-2]，比p小的数不可能整除于p，所以x-y的质因数分解中不包含p。

       矛盾，所以此数列模p所得结果互不相同。

      

       由于数列模p所得结果互不相同，此数列共p-1个元素，任何数模p的结果共p-1种，故数列模p所得结果恰好包含模p的所有结果，既不重复，也不遗漏。

       考虑将此数列逐项相乘，将模p的所有结果相乘，结合模运算的性质，我们有：

这是在说(p-1)!*a^(p-1)除以p的余数与(p-1)!除以p的余数相等，注意到(p-1)!一定不整除于p，所以我们有：

       这就是费马小定理。

对于第二题，离散对数的表示太恐怖了，所以我们要把这个表示化回我们熟悉的样子。

       从简单处入手，我们设（均为模p意义下）：

       所以有

       第二题等式左边有bc，所以我们凑出bc：

       注意到第二题满足费马小定理的条件，由于费马小定理的思想，我们进行简化：

       所以原式可化为

       由费马小定理，即

       根据离散对数的定义，即

       即
 

         即证。

对于第三题，我们同样首先作简化

       将y1y2代回，原式化为：

       又因为：

       即：
 

         代回原式，即：

       整理：

       由费马小定理：

       这是恒等式，即证。

欧拉定理

事实上，费马小定理是欧拉定理的特殊情况。

欧拉定理是这样的：记欧拉函数是小于n的正整数中与n互质的数的数目，为φ(m)。其中φ(n)=n(1-1/p1)(1-1/p2)(1-1/p3)…(1-1/pm)，p1、p2……pm是n的因数。

当n>1且gcd(a,n)=1时，有：

令n为质数p，小于p的正整数中与p互质的数的数目为p-1，我们得到费马小定理。

公钥加密系统

       让我们重看第三题。本题的背景实际上是EIGamal公钥密码体制。在上述的过程中，我们从没有计算过离散对数的具体数值，这不止是因为其表述复杂，更是因为其具体运算人力不可及。

       在EIGamal公钥密码的实际运用中，其安全性正是基于离散对数难以求解。

       在下式：

n实际上是随意指定的，b是通过（a,p,n）组成的数对计算出来的，因为模的计算性质良好，可以通过快速幂等方式迅速地解出下式

的值，即b的值。

所以，我可以向外界公开告知所有人自己的a与p的信息。

现在有一个用户Bob希望与我进行沟通，他自行生成一个n，基于（a,p,n）生成b，并将b传递给我。因为n始终没有对外传递过，通过b计算n的离散对数计算问题是难以求解的，所以其他人即使拿到了b也没有办法获得信息。

我收到了b之后，想将x作为信息传递给Bob，所以我自行生成一个k，根据题意分别计算y1与y2，并将其传递给Bob，因为k始终没有对外传递过，通过y1与y2计算x的离散对数计算问题是难以求解的，所以其他人即使拿到了y1与y2也没有办法获得信息。

Bob收到y1与y2之后，通过题中所给式子，结合自己的n进行运算，经过我们之前的求解，我们知道x是可以在Bob这里计算出来的。

至此，完成了一次信息x从我传递到Bob的过程，同时可以极大程度上保证x只有我与Bob可以知道。

       在上述过程中，（a,p）被称为公钥，n是Bob的私钥。这就是公钥加密系统的基本思想。当然这样的表述遗漏了大量细节，有兴趣的读者可以自行查阅相关资料。

后话

大名鼎鼎的RSA也是一种公钥加密算法。RSA的安全性依赖于两个大素数乘积的分解是困难的。

也许我们可以这么认为，只要能找到一个性质良好的运算使得运算本身易于计算而逆运算困难，我们就可以基于这种运算设计一种公钥加密算法。

你还能找到其他运算吗？