1.PID的介绍

【案例1】: 推动1kg的物体从原点到1米处，水平方向，无摩擦：

1. 只用比例(P)控制：PGain=20;，即F = 20 * (1 - x)。 

下图在matlab中仿真可见其是震荡的。就是不考虑摩擦，小于目标位置1m时，力都是向右的，达到目标位置，力为0，但是因为有速度存在，还是会过冲过去。因为0-1米过程中力产生的动能，需要在1-2米路程中被相反的力消耗掉。可以想象人荡秋千的情况，如果没有空气阻力，则一直会荡下去。

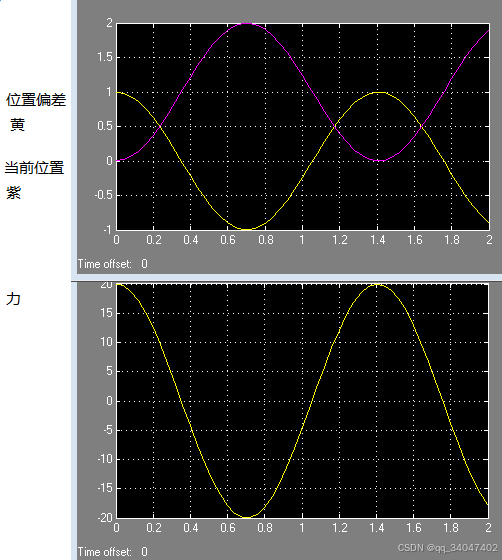
2 需要增加微分(D)控制.微分相当于提前刹车。因为靠近1的过程中err=1-X; X增大，err是变小的。err的微分是负数。让控制力变小。

F = kp * err + Td* err' = k * (1 -x) + Td * (1-x)'

因为 err = 1 - x 在0-1米过程中,随着x靠近1米的目标位置，err 是越来越小的，即err求导是负值。相当于微分的加入让向右的力小了一些。即提前刹车了，而且速度越快微分导致力减小的越多。

实验如下：.可见加入微分后，因为提前刹车，相当于增加了阻尼，会稳定下来。

PGain=20. DGain=3

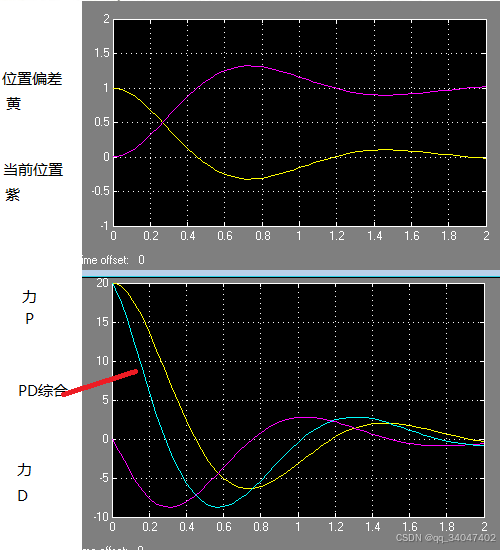
3 因为本例在停在目标位置时，力=0即可，即不需要维持力，积分项为0即可

【案例2】:把1kg(9.8N)的物体从地面拉起到1米高处

1 只用P控制：PGain=20; 即F = 20*(1-x),

此时因为比例系数偏小，因为到0.5m时，0.5*20=10N差不多已经等于下面的重量，但因为有速度存在，还是向上走但是已经开始减速了。而且到达比如1m的位置时拉力 F=0,但是重力会让它向下走

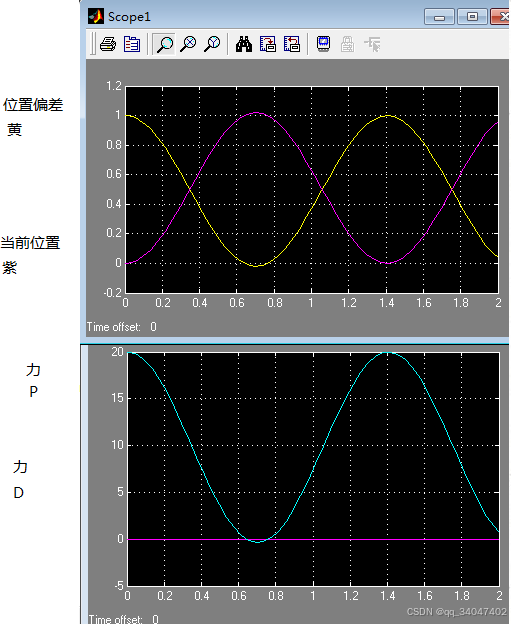
2.增大比例系数

增大比例系数到40.仍然震荡，只是最高可以上升到1.5米左右

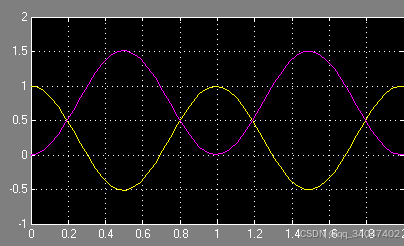
.3 增加微分D控制

PGain=40； DGain=3；

F = kp * err + Td* err' = 40 * (1 -x) + 3 * (1-x)'

差不多稳定在0.755的位置，因为：40*(1-0.755)=9.8N正好等于重力。

虽然稳定，但是离目标位置1米，有0.245m的偏差，该偏差与比例系数的乘积 = 稳定所需的重力

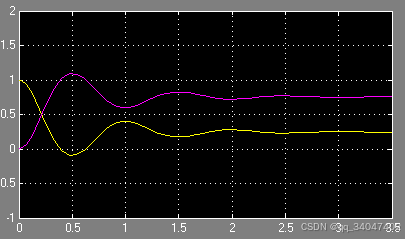
4.增加积分(I)控制

F = kp * err + Td* err' + 1/Ti * (err积分)

积分消除稳态误差的原理是因为 只要没有达到目标位置，err就累加，会增大F，让它向目标位置靠近。

P=40； I=20；D=3；

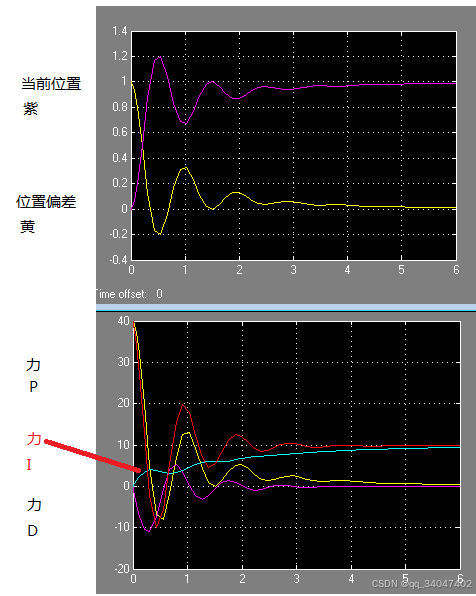
【积分饱和的问题】

在P=40； I=20；D=3；的情况下，但是如果去距离20m的位置；

因为开始偏差太大，去目标值20m花费时间很长，导致积分数值很大，导致积分项很大

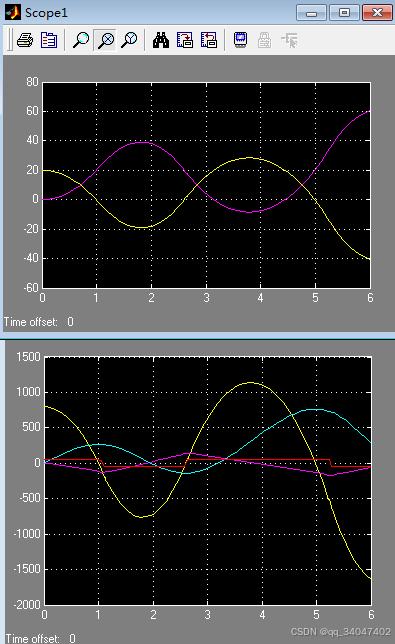
解决积分饱和的方法很多，比如限制积分的范围，在接近目标的区域才开始积分。比如偏差在4m的时候进行积分。那么就可以稳定

【已有知识的利用】

比如我知道它是9.8N左右。直接用下面的式子也可以。不过此时所需比例系数肯定要小很多。

F = 9+ kp * err + Td* err' + 1/Ti * (err积分)