【题目1】甲和乙约定周日早上在学校门口见面,当天先到者等未到者20分钟,超过20分钟对方未到就离开.甲乙均在12点到13点之间任意时刻到达学校门口,则两人可以碰面的概率是多少?
解答:
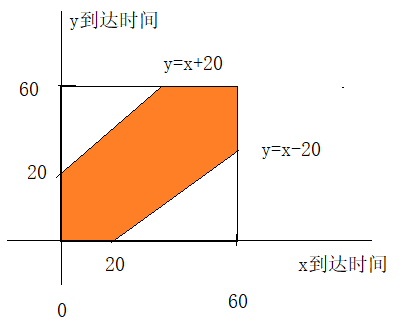
假设甲同学到达学校时是12点后的x分钟这个时刻。
乙同学则必须在12点后的y分钟,如果要见面,y必须在 [x-20, x+20]这个时间范围内。
即: y>=x-20 且 y<=x+20.
即y最多提前20分钟,最多延后20分钟。
图上看:总的面积是60*60; 可能见面的区域面积:60*60 - 40*40
即见面概率:(60*60-40*40)/(60*60)=5/9 = 55.56%.

























 3576
3576

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










