连续离散混合系统控制与仿真

摘要 以二阶积分器串联型系统为例，分析了混杂系统的控制器参数设计方法，比较了控制器周期对控制效果的影响，仿真展示了简单混杂系统的良好控制效果，并与纯连续系统与纯离散系统对比，得出的结论是混杂系统的设计方法与纯连续/离散系统区别非常大。

简单二阶系统

先研究最简单的二阶积分器串联型系统
$$\begin{array}{rl}& {\dot{x}}_1=x_2\\ & {\dot{x}}_2=u\end{array}$$
使用零阶保持法离散化（见附录），
$$A=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right],B=\left[\begin{array}{c}0\\ 1\end{array}\right]$$
设控制器周期（即离散化周期）为 $T$ 已知，则矩阵指数
$$\begin{array}{rl}& (sI-A{)}^{-1}={\left[\begin{array}{cc}s& -1\\ 0& s\end{array}\right]}^{-1}=\frac{1}{s^2}\left[\begin{array}{cc}s& 1\\ 0& s\end{array}\right]\\ & {\text{e}}^{At}={\mathcal{L}}^{-1}(sI-A{)}^{-1}={\mathcal{L}}^{-1}\left[\begin{array}{cc}\frac{1}{s}& \frac{1}{s^2}\\ 0& \frac{1}{s}\end{array}\right]=\left[\begin{array}{cc}1& t\\ 0& 1\end{array}\right]\\ & F={\text{e}}^{AT}=\left[\begin{array}{cc}1& T\\ 0& 1\end{array}\right]\\ & G={\int }_0^T{\text{e}}^{At}\text{d}tB=\left[\begin{array}{cc}T& \frac{T^2}{2}\\ 0& T\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{T^2}{2}\\ T\end{array}\right]\end{array}$$
于是
$$\begin{array}{rl}\vec{x}(n+1)=& F\vec{x}(n)+Gu(n)\\ =& \left[\begin{array}{cc}1& T\\ 0& 1\end{array}\right]\vec{x}(n)+\left[\begin{array}{c}\frac{T^2}{2}\\ T\end{array}\right]u(n)\end{array}$$
将
$$u(n)=-K\vec{x}(n)=-\left[\begin{array}{cc}{k}_1& k_2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$
代入得
$$\begin{array}{rl}\vec{x}(n+1)=& (F-GK)\vec{x}(n)\\ =& \left(\left[\begin{array}{cc}1& T\\ 0& 1\end{array}\right]+\left[\begin{array}{cc}\frac{T^2}{2}{k}_1& \frac{T^2}{2}{k}_2\\ T{k}_1& T{k}_2\end{array}\right]\right)\vec{x}(n)\end{array}$$
给定两个极点就可以使用比较系数法计算出 $k_1,k_2$。除此以外还有一种便于使用计算机求解的方法
$$K=\left[\begin{array}{cccc}0& \cdots & 0& 1\end{array}\right]{\left[\begin{array}{ccc}G& FG& F^{n-1}G\end{array}\right]}^{-1}\alpha (F)$$
其中 $\alpha (x)$ 为给定极点的特征多项式，例如给定两个极点为 ${\lambda }_1,{\lambda }_2$，则 $\alpha (x)=(x-{\lambda }_1)(x-{\lambda }_2)$。设给定重极点 ${\lambda }_1={\lambda }_2=-5$，变换到离散域 $z={\text{e}}^{sT}={\text{e}}^{-0.5}\approx 0.6$，计算出 $K=[16,7.2]$。仿真结果如图所示，图中 $u$ 为控制量，$y=x_1$ 为状态量。

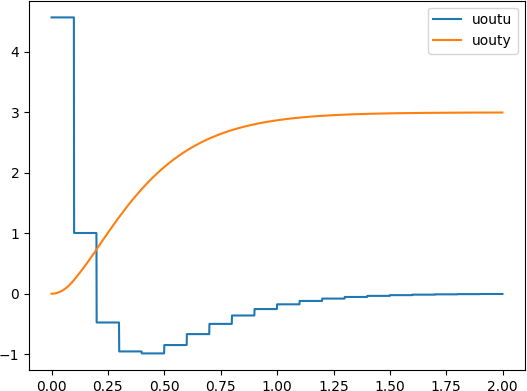
与纯连续系统比较

  还是这个二阶系统，当闭环传递函数的极点取到左半平面无穷远时系统响应性能最好，也就是在离散域中两个极点都取到原点时，过渡时间最短而且没有超调，在这个例子中 $T=0.1$ 时 $K=[100,15]$。但是观察系数 $K$ 的取值可以注意到跟纯连续系统有很大区别。对二阶积分器串联型系统
$$G(s)=\frac{1}{s^2},\ddot{x}=u$$
设计控制律 $u=-k_{p}x-k_d\dot{x}$，闭环传递函数为
$$\frac{1}{s^2+k_{d}s+k_p}$$
取 $k_d=2k_p$ 且两个系数无穷大时就可以使系统响应时间无限短而且没有超调，但是当控制器离散化以后，这个例子中 $k_p=100,k_d=15$，与纯连续系统完全对不上。
  那么当 $T\to 0$ 的时候混杂系统是否跟纯连续系统等价？实际上也不是。不妨算一下 $K$ 的表达式
$$\begin{array}{rl}K=& [01][GFG{]}^{-1}{F}^2\\ =& [01]{\left[\begin{array}{cc}\frac{T^2}{2}& \frac{3T^2}{2}\\ T& T\end{array}\right]}^{-1}\left[\begin{array}{cc}1& 2T\\ 0& 1\end{array}\right]\\ =& [01]\left[\begin{array}{cc}-\frac{1}{T^2}& \frac{3}{2T}\\ \frac{1}{T^2}& -\frac{1}{2T}\end{array}\right]\left[\begin{array}{cc}1& 2T\\ 0& 1\end{array}\right]\\ =& \left[\begin{array}{cc}\frac{1}{T^2}& \frac{3}{2T}\end{array}\right]\end{array}$$
当 $T\to 0$ 时，$k_d/k_p\to 0$ 而不是 $2$。
  但采样周期 $T$ 小了是有好处的。同样取最优的参数 $K$，当 $T$ 分别取 $0.1$ 和 $1$ 时的仿真结果如图所示。


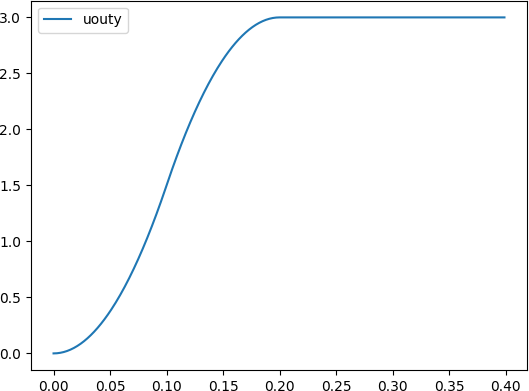
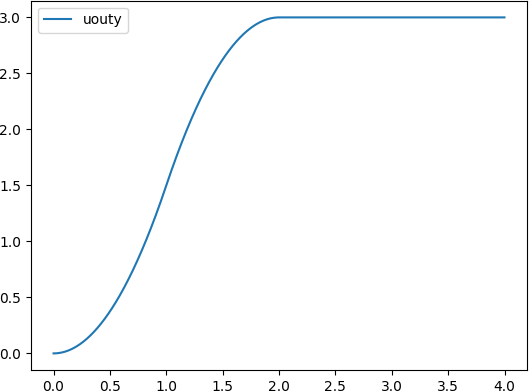
可以看出两条曲线完全相同，只是时间尺度差了10倍。

与纯离散系统比较

  作为参考，下面再算一下纯离散系统，用最简单的欧拉离散法
$$\begin{array}{rl}& x_1(n)=x_1(n-1)+T{x}_2(n)\\ & x_2(n)=x_2(n-1)+Tu(n)\end{array}\text{\hspace{1em}(1)}$$
被控对象传递函数为
$$G(z)={\left(\frac{T}{1-z^{-1}}\right)}^2=\frac{T^2}{1-2z^{-1}+z^{-2}}$$
设计控制律
$$u(n)=k_1[r(n-1)-x(n-1)]+k_2[r(n-2)-x(n-2)]$$
则
$$(1-2z^{-1}+z^{-2})x(z)=T^{2}u(z)=T^2[(k_1{z}^{-1}+k_2{z}^{-2})r(z)-(k_1{z}^{-1}+k_2{z}^{-2})x(z)]$$
闭环传递函数为
$$\frac{T^2(k_1{z}^{-1}+k_2{z}^{-2})}{1+(T^2{k}_1-2)z^{-1}+(T^2{k}_2+1)z^{-2}}$$
设给定闭环极点为$z_1=z_2=0.1$，则 $T^2{k}_1=1.8$，$T^2{k}_2=-0.99$
代码和仿真结果如下

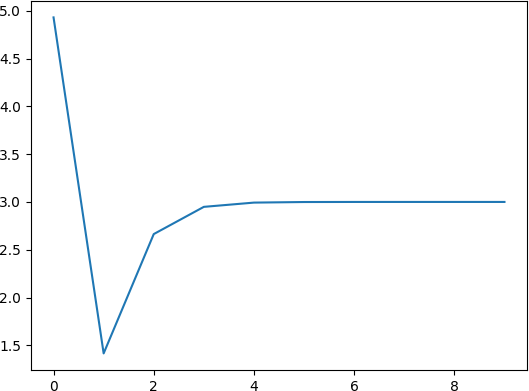
import matplotlib.pyplot as plt
x1, x2 = 2, 5
T = 0.1
xn1 = xn2 = 0
plotx1 = []
for n in range(10):
    u = (3-xn1) * (1.8/T**2) + (3-xn2) * (-0.99/T**2)
    x2 += T*u
    x1 += T*x2
    xn2 = xn1
    xn1 = x1
    plotx1.append(x1)
plt.plot(plotx1)
plt.show()

可以看出 $k_1$ 和 $k_2$ 里甚至会有负数。我见过很多人仿真的时候要么用纯连续系统要么用纯离散系统，这两种做法都不对。除非实际的控制器和被控对象就是纯连续或纯离散，否则用纯连续或纯离散的理论研究混杂系统会严重影响控制效果。

离散系统的一个坑

  前一节离散系统中用于描述被控对象式(1)的代码中的第8，9行代码

x2 += T*u
x1 += T*x2

没有写反，如果写反的话就错了，变成了对下面系统的描述
$$\begin{array}{rl}& x_1(n)=x_1(n-1)+T{x}_2(n-1)\\ & x_2(n)=x_2(n-1)+Tu(n)\end{array}$$
这个问题困扰了我一个多小时。

参考

教材[1]里有更完整的推导过程，链接[2]里有另一个混合系统控制的例子。[3]和[4]是两本书专门讲这个，等有空看看在补充。

1. 孙增圻. 计算机控制理论与应用. 清华大学出版社.
2. simucpp系列教程(3)例程解析(第二部分)
3. Hybrid Dynamical Systems: Fundamentals and Methods
4. Hybrid Dynamical Systems: Modeling, Stability, and Robustness

附录：零阶保持器离散化

对使用状态空间描述的线性系统
$$\begin{array}{l}{\vec{x}}^{\prime }=A\vec{x}+Bu\\ y=C\vec{x}+Du\end{array}$$
使用零阶保持法可以离散化成
$$\begin{array}{l}\vec{x}(k+1)=F\vec{x}(k)+Gu(k)\\ y(k)=C\vec{x}(k)+Du(k)\end{array}$$
其中
$$F={\text{e}}^{AT},G={\int }_0^T{\text{e}}^{At}\text{d}tB$$
${\text{e}}^{AT}$ 是矩阵指数。
推导
$$\begin{array}{rl}& x^{\prime }(t)=Ax(t)+Bu(t)\\ & x(t)={\text{e}}^{A(t-t_0)}x(t_0)+{\int }_{t_0}^t{\text{e}}^{A(t-\tau )}Bu(\tau )\text{d}\tau \end{array}$$
令$t_0=kT$，$t=(k+1)T$，则
$$\begin{array}{rl}& x((k+1)T)={\text{e}}^{AT}x(kT)+{\int }_{kT}^{(k+1)T}{\text{e}}^{A(kT+T-\tau )}Bu(\tau )\text{d}\tau \\ & {\int }_{kT}^{(k+1)T}{\text{e}}^{A(kT+T-\tau )}Bu(\tau )\text{d}\tau \stackrel{t=kT+T-\tau }{=}{\int }_0^T{\text{e}}^{At}Bu(kT+T-t)\text{d}t\\ & x(k+1)={\text{e}}^{AT}x(k)+{\int }_0^T{\text{e}}^{At}B\text{d}tu(k)\end{array}$$

附录：代码

计算反馈控制系数 $K$ 的代码

#include <iostream>
#include "zhnmat.hpp"
using namespace zhnmat;
using namespace std;
typedef std::vector<double>  vecdble;
Mat polynomial(Mat x, vecdble lambda) {
    double order = x.row();
    if (order != x.col()) return Mat();
    Mat ans = eye(order);
    for (uint32_t i = 0; i < order; i++)
        ans *= x - lambda[i]*eye(order);
    return ans;
}
int main(void) {
    double T = 0.1;
    Mat F(2, 2, vecdble{1, T, 0, 1});
    Mat G(2, 1, vecdble{T*T*0.5, T});
    Mat K = HConcat(G, F*G).inv().atr(1);
    K *= polynomial(F, vecdble{0.6, 0.6});
    cout << K << endl;
}

二阶积分器串联型系统仿真代码

#include "simucpp.hpp"
using namespace simucpp;
int main() {
    Simulator sim1;
    FUIntegrator(uint1, &sim1);
    FUIntegrator(uint2, &sim1);
    FUConstant(cnst1, &sim1);
    FUOutput(uout1, &sim1);
    sim1.connectU(cnst1, uint1);
    sim1.connectU(uint1, uint2);
    sim1.connectU(uint2, uout1);
    sim1.Initialize();
    double ctrl;
    for (uint32_t n1 = 0; n1 < 20; n1++) {
        ctrl = (3-uint2->Get_OutValue()) * 15.24;
        ctrl -= uint1->Get_OutValue() * 7.04;
        for (uint32_t i = 0; i < 100; i++) {
            cnst1->Set_OutValue(ctrl);
            sim1.Simulate_OneStep();
        }
    }
    sim1.Plot();
    return 0;
}