【CNN】卷积层参数与输入输出大小计算说明

基本计算公式

$W$为输入大小，$F$为卷积核大小，$P$为填充大小(padding)，$S$为步长(stride)，$N$为输出大小。有如下计算公式：$$N=\frac{(W-F+2P)}{S}+1$$
由上述公式很容易推得一些常用的卷积层参数——输入输出的大小不变，仅通道数量改变。

# 一个卷积核大小为5*5的卷积层参数
kernel_size = 5
stride = 1
padding = 2
# 一个卷积核大小为3*3的卷积层参数
kernel_size = 3
stride = 1
padding = 1

更简单地，若步长为1，填充大小只要满足下述公式，输入输出的大小就是一致的：$$P=\frac{F-1}{2}$$

注意事项

若输入输出的长与宽不一样，只需要分别计算就可以了，可以灵活地依据公式调整卷积核大小以及其他参数值。

• 计算示例：
  现有 (800，1000) 的输入，想要得到 (600，800) 的输出，卷积核设定为 (3,5)，步长设定为 2，那么需要如何设置padding得到想要的输出？
  代入上式计算显然有(向上舍入)：$$P_h=\frac{(600-1)\ast 2+3-800}{2}=201$$ $$P_w=\frac{(800-1)\ast 2+5-1000}{2}=302$$

#input size (800,1000)
kernel_size=(3,5),       
stride=2,                
padding=(201,302),
#output size (600,800)

总而言之，调整卷积核大小、步长或者填充大小都可以改变输出大小，但考虑到网络有效性问题，一般kernel_size依据经验设置为常用的 (5,5) 或是 (3,3) 或是 (3,3)+(1,3)+(3,1) 等，而padding也不会太大，stride也一般为1或者2。当然，各种各样的网络结构还是都有去尝试的价值。

说明

如下面所示，一个长度为6的像素块，若卷积核大小为3，步长为1，则需要填充2个像素点才能使做卷积后的长度依旧为6。

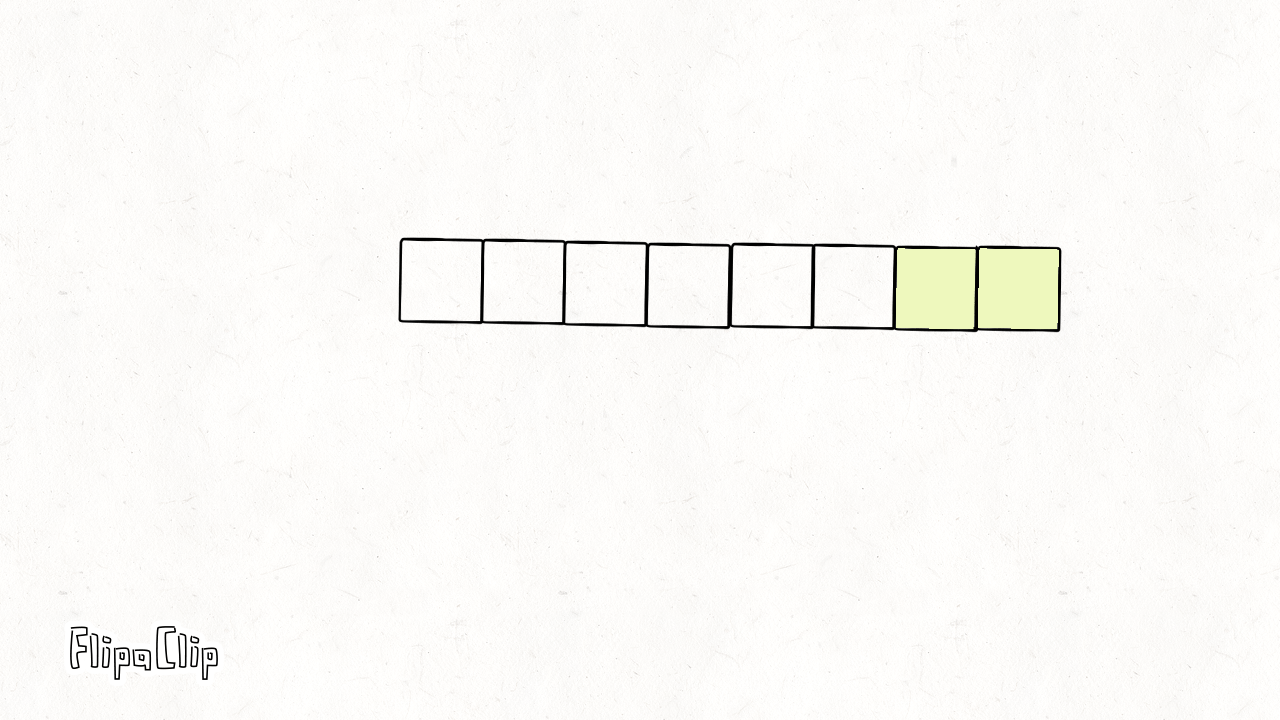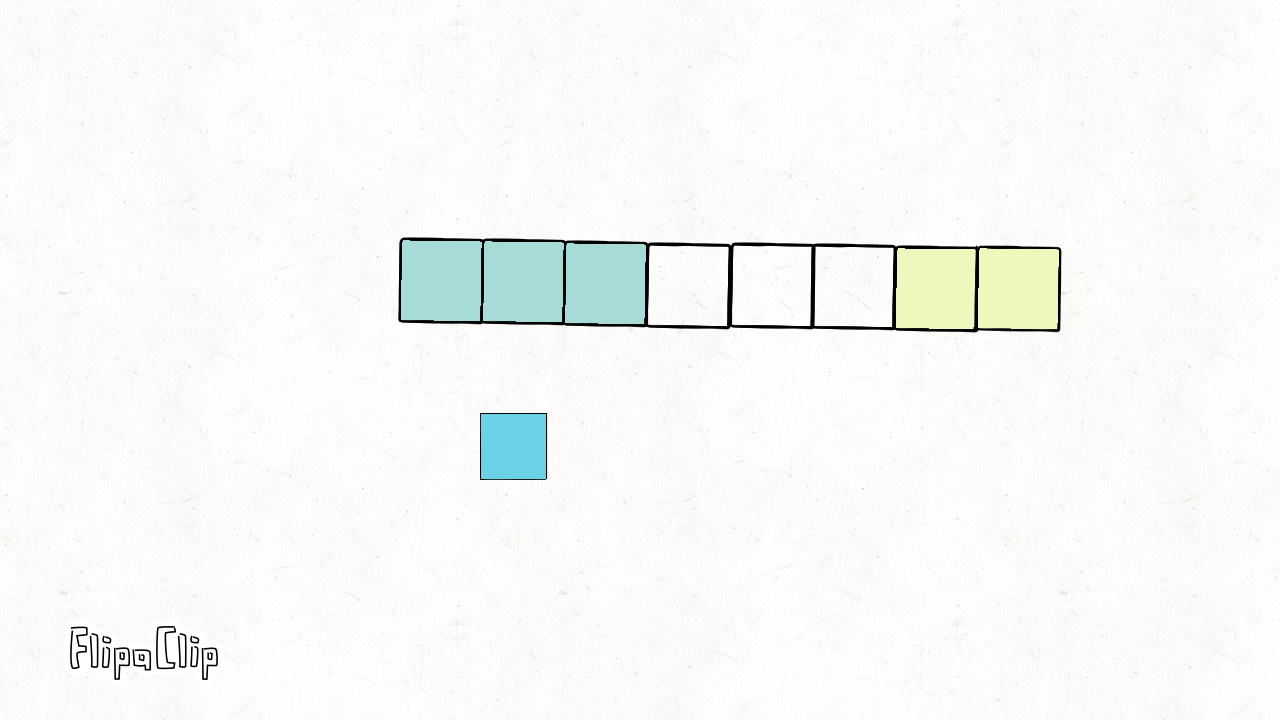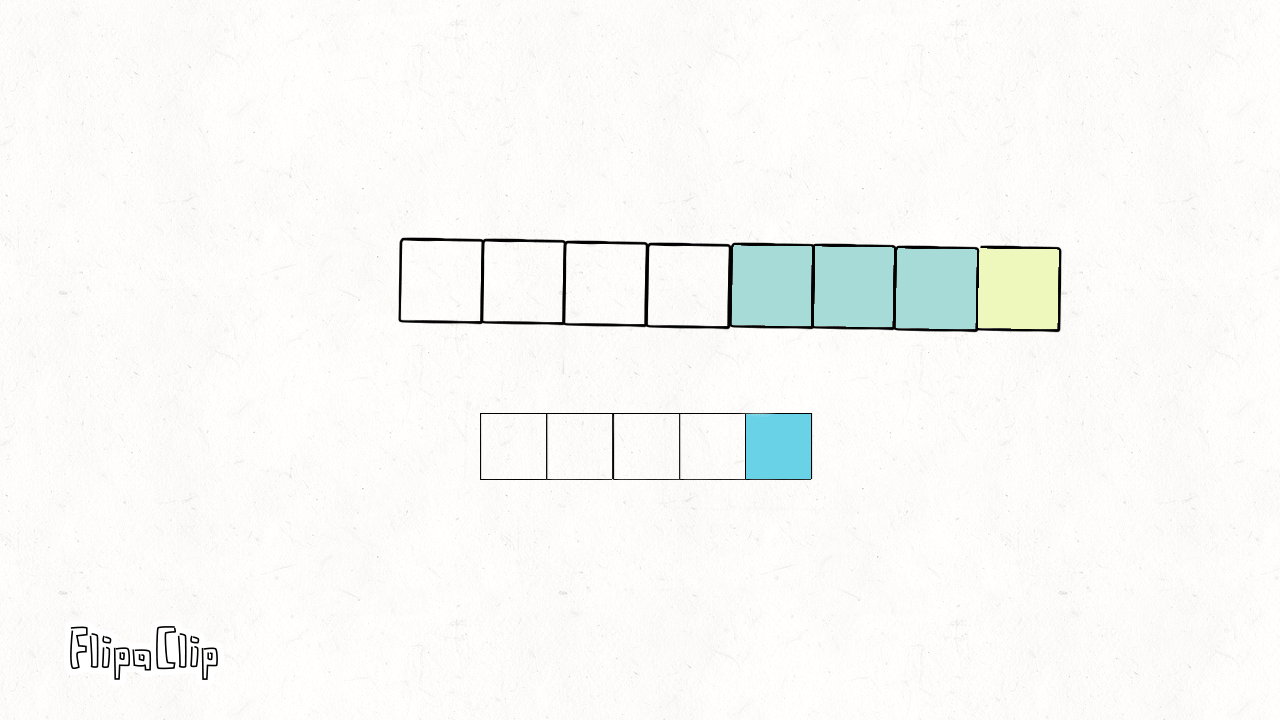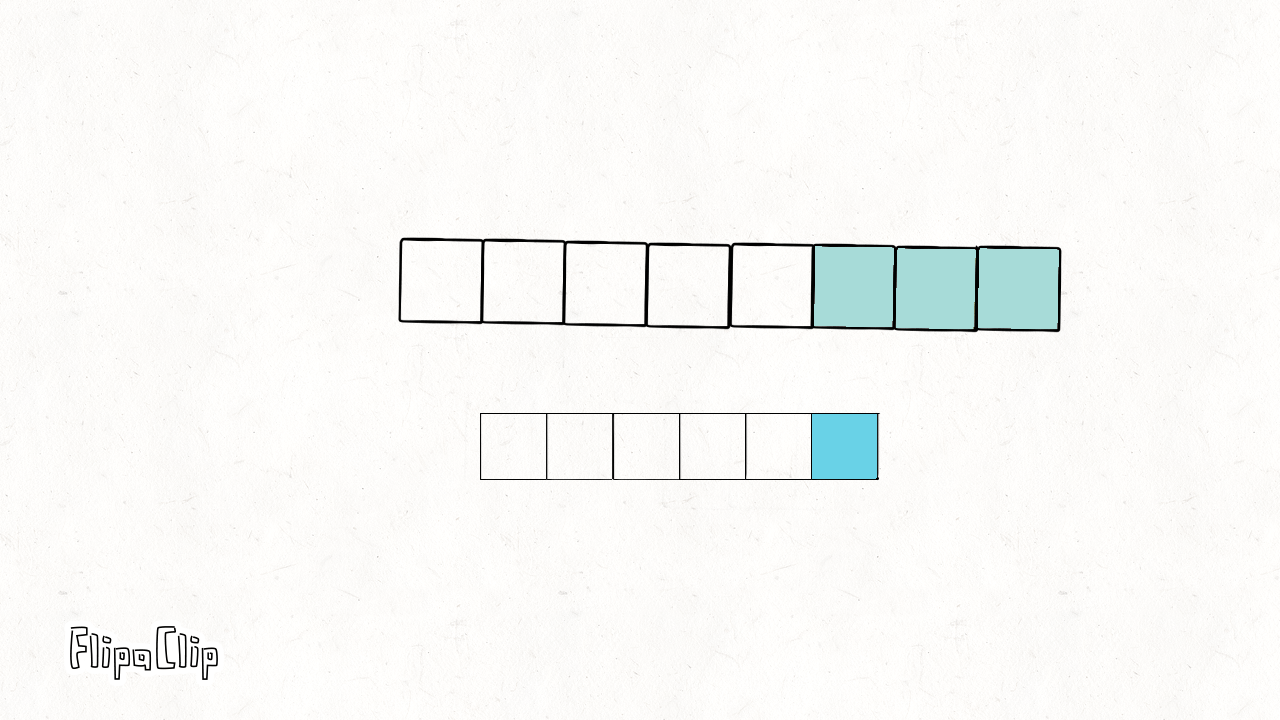
逆卷积计算

在上采样中需要用到逆卷积运算，此类运算可以实现矩阵的扩展。现有$W$为输入大小，$F$为卷积核大小，$P_i$为输入填充大小，$P_o$为输出填充大小，$S$为步长，有如下公式计算输出大小$N$：
$$N=(W-1)\ast S+P_o-2P_i+F$$
在pytorch下可以这样写：

# input (n,32,height,width)
self.deconv = nn.ConvTranspose2d(
				32, 1, 
				kernel_size=3, 
				stride=2, 
				padding=1, 
				dilation=1, 	# 卷积核元素间距
				output_padding=1)
# output (n,1,height*2,width*2)

关于逆卷积的详细操作，以后有时间再补充