在写这篇文章之前,先说一些题外话。
许多机器学习算法(如后面将要提到的LDA)涉及的数学知识太多,前前后后一大堆,理解起来不是那么容易。
面对复杂的机器学习模型,尤其是涉及大量数学知识的模型,我们往往要花费大量的时间和精力去推导数学算法(公式),如果过分沉湎于此会忽略了很多背后也许更重要的东西,正所谓只见树木,不见森林,而这是缺乏远见,是迷茫的。
我们需要深入理解模型背后的逻辑和所蕴含的或简或繁的思想。某些思想甚至可能是很美的思想,很伟大的思想。这些理解,使得面对复杂的问题时候,面对陌生问题时,会左右我们的选择。我们会首先想起谁,谁是我们工具箱里最得心应手的工具,就像自己的孩子一样亲切。而有些方法我们注定不喜欢,也用不太懂。毕竟我们不是每个人都会去写复杂的机器学习算法code,尤其是复杂的分布式code,但也不意味着我们不需要关注模型的数学原理,因为没这些数学原理的支撑,也许你永远理解不了这个模型。但是仅仅掌握公式的推导甚至从头到尾能写出完整代码,也还是远远不够的。比如说我们都知道为了控制over-fitting,需要正则化,为什么在看似很精确的公式里面硬生生的多加入一个正则项,就能够达到控制over-fitting的目的呢?又如何判断所选择的正则化参数是合理的?不大也不小,刚好合适。公式我们都能完整的推导吧,但也许有些事我们想的还是不那么明白,用的时候自然也就会有一些疑虑。
所以呢,要做到深入浅出真的很难,这也是我们学习ML需要努力的方向,理解这些ML模型背后的逻辑,所蕴含的美,所表达的的思想,甚至是哲理,也许能助你我成长到一个新的高度。
好了,言归正传。在Spark2.0版本中(不是基于RDD API的MLlib),共有四种聚类方法:
(1)K-means
(2)Latent Dirichlet allocation (LDA)
(3)Bisecting k-means(二分k均值算法)
(4)Gaussian Mixture Model (GMM)。
基于RDD API的MLLib中,共有六种聚类方法:
(1)K-means
(2)Gaussian mixture
(3)Power iteration clustering (PIC)
(4)Latent Dirichlet allocation (LDA)**
(5)Bisecting k-means
(6)Streaming k-means
多了Power iteration clustering (PIC)和Streaming k-means两种。
本文将介绍LDA主题建模,其它方法在我的整个系列中都会有介绍。
什么是LDA主题建模?
隐含狄利克雷分配(LDA,Latent Dirichlet Allocation)是一种主题模型(Topic Model,即从所收集的文档中推测主题)。 甚至可以说LDA模型现在已经成为了主题建模中的一个标准,是实践中最成功的主题模型之一。那么何谓“主题”呢?,就是诸如一篇文章、一段话、一个句子所表达的中心思想。不过从统计模型的角度来说, 我们是用一个特定的词频分布来刻画主题的,并认为一篇文章、一段话、一个句子是从一个概率模型中生成的。也就是说 在主题模型中,主题表现为一系列相关的单词,是这些单词的条件概率。形象来说,主题就是一个桶,里面装了出现概率较高的单词(参见下面的图),这些单词与这个主题有很强的相关性。
LDA可以用来识别大规模文档集(document collection)或语料库(corpus)中潜藏的主题信息。它采用了词袋(bag of words)的方法,这种方法将每一篇文档视为一个词频向量,从而将文本信息转化为了易于建模的数字信息。但是词袋方法没有考虑词与词之间的顺序,这简化了问题的复杂性,同时也为模型的改进提供了契机。每一篇文档代表了一些主题所构成的一个概率分布,而每一个主题又代表了很多单词所构成的一个概率分布。
LDA可以被认为是如下的一个聚类过程:
(1)各个主题(Topics)对应于各类的“质心”,每一篇文档被视为数据集中的一个样本。
(2)主题和文档都被认为存在一个向量空间中,这个向量空间中的每个特征向量都是词频(词袋模型)
(3)与采用传统聚类方法中采用距离公式来衡量不同的是,LDA使用一个基于统计模型的方程,而这个统计模型揭示出这些文档都是怎么产生的。
Latent Dirichlet allocation (LDA) is a topic model which infers topics from a collection of text documents. LDA can be thought of as a clustering algorithm as follows:
(1)Topics correspond to cluster centers, and documents correspond to examples (rows) in a dataset.
(2)Topics and documents both exist in a feature space, where feature vectors are vectors of word counts (bag of words).
(3)Rather than estimating a clustering using a traditional distance, LDA uses a function based on a statistical model of how text documents are generated.
下面的几段文字来源于:http://www.tuicool.com/articles/reaIra6
它基于一个常识性假设:文档集合中的所有文本均共享一定数量的隐含主题。基于该假设,它将整个文档集特征化为隐含主题的集合,而每篇文本被表示为这些隐含主题的特定比例的混合。
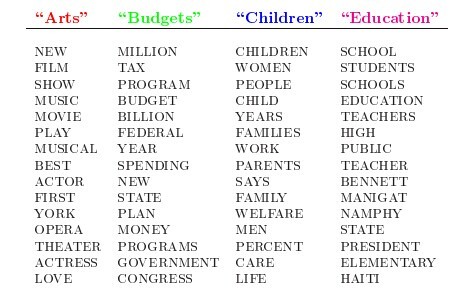
LDA的这三位作者在原始论文中给了一个简单的例子。比如给定这几个主题:Arts、Budgets、Children、Education,在这几个主题下,可以构造生成跟主题相关的词语,如下图所示:
然后可以根据这些词语生成如下图所示的一篇文章(其中不同颜色的词语分别对应上图中不同主题下的词)
表面上理解LDA比较简单,无非就是:当看到一篇文章后,我们往往喜欢推测这篇文章是如何生成的,我们可能会认为某个作者先确定这篇文章的几个主题,然后围绕这几个主题遣词造句,表达成文。
前面说了这么多,在推导模型前,总结几条核心思想:
(1)隐含主题,形象的说就是一个桶,里面装了出现概率较高的单词,从聚类的角度来说,各个主题(Topics)对应于各类的“质心”,主题和文档都被认为存在于同一个词频向量空间中。(2)在文档集合中的所有文本均共享一定数量的隐含主题的假设下,我们将寻找一个基于统计模型的方程。
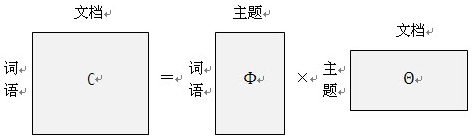
LDA的核心公式如下:
d
代表某篇文档,
上面式子的左边,就是文档的词频,是很容易统计得到的。如果一篇文章中有很多个词语,那么就有很多个等式了。再如果我们收集了很多的文档,那么就有更多的等式了。这时候就是一个矩阵了,等式左边的矩阵是已知的,右边其实就是我们要求解的目标-与隐含主题相关,图示如下:
下面来看一段很概述性的文字:
LDA是一个层次贝叶斯模型,把模型的参数也看作随机变量,从而可以引入控制参数的参数,实现彻底的“概率化”。LDA模型的Dirichlet的先验分布,文档d上主题的多项式分布。目前,参数估计是LDA最重要的任务,主要有两种方法:Gibbs抽样法(计算量大,但相对简单和精确)和变分贝叶斯推断法(计算量小,精度度弱)。
看来关于LDA的数学求解,还有很多知识要学习,只好稳打稳扎,一步一步来了。大家还可以参考rickjin《LDA数学八卦》*一文。
一些数学铺垫
参数估计(parameter estimation)
用系统理论的语言来看:在已知系统模型结构时,用系统的输入和输出数据计算系统模型参数的过程。18世纪末德国数学家C.F.高斯首先提出参数估计的方法,他用最小二乘法计算天体运行的轨道。20世纪60年代,随着电子计算机的普及,参数估计有了飞速的发展。参数估计有多种方法:矩估计、极大似然法、一致最小方差无偏估计、最小风险估计、同变估计、最小二乘法、贝叶斯估计、极大验后法、最小风险法和极小化极大熵法等。最基本的方法是最小二乘法和极大似然法(来自百度百科,百度百科倒是经常贴“高大上”的描述方法,但是有些东西怎么看却都是前言不接后语,连个公式渲染都没有,好歹简单学学wikipedia,让中国人上网查个数学公式贼费劲,还乱七八糟的都不标准不统一,吐槽一下,呵呵)。
从系统理论角度出发比较“高大上”,说的也比较抽象,但是考虑到任何机器学习模型也可以理解为一个系统,上面那段话好好理解一下也挺好,我们可以提取出下面一些理解:
(1)参数估计并不是数理统计里面一个特有的术语,一上来就看数理统计里面的参数估计,就太狭隘了,也就没有那么深入的理解。但是也不可否认,参数估计很多方法都是数理统计的方法,但也不全是,如著名的最小二乘法(在那里都能见到这哥们的影子)。
(2)既然都开始估计参数了,那么模型的结构肯定是已知的,也就是说:机器学习选取什么算法,决策树?还是SVM?还是Beyes概率的,深度学习的?,你自己其实已经有主意了的,手头上有一些样本数据(观测值),任务是怎么去求解(优化)系统(模型)的参数。
正是由于最小二乘法和极大似然法也是ML里面最基本的使用广泛的参数估计方法,我们需要重点掌握。
另外从数理统计学的语言讲: 参数估计是根据从总体中抽取的样本估计总体分布中包含的未知参数的方法。人们常常需要根据手中的数据,分析或推断数据反映的本质规律。即根据样本数据如何选择统计量去推断总体的分布或数字特征等。统计推断是数理统计研究的核心问题。
可以看出:
(1) 正是由于我们往往只能获得一少部分样本,却被要求拿来估计复杂系统的真实参数,所以数学家才会根据不同的模型,应用于不同的数据情况下,设计出如此多的巧妙办法,尽量使估计“无偏,一致,有效”。
(2)数理统计学里面的参数估计目的更加明确,即推断总体的分布,如总体概率密度函数的类型及参数,总体样本的统计参数(均值、方差等等)。显然机器学习的目标更加远大,我们需要估计各类复杂模型的参数,当然也包括一部分以概率统计理论为基础的ML模型(比如本文后面要介绍的GMM和LDA)。
联合概率分布 Joint probability distribution
首先推荐一篇博文:zouxy09的CSDN 在里面多个生动的例子的帮助下,比较容易看懂很多概念:
从最大似然到EM算法浅解 http://blog.csdn.net/zouxy09/article/details/8537620/
概率方法的很多公式都很长,看起来挺吓人,很多时候其实都是由于采用的是联合概率分布,对他的形式把握透彻了,这些公式其实没有那么难理解。
很多时候(比如说朴素Beyes分类器),会简化问题,首先做独立性假设,虽然可能并不完全满足独立性假设,也都这样做,而且发现有很好的鲁棒性。
独立性假设就是:一个事件发生概率不受其他事件影响的事件.两(多)个独立事件同时发生的概率等于两(多)者分别发生的概率之积.假如
A
、
如果我们抽取了
N
个样本,那么可以认为是发生了
设
x1,x2,...,xN
是从概率密度函数
p(x;θ)
中随机抽取的
N
个样本,从而得到联合概率密度函数
p(xn,θ) 代表概率密度函数的参数为 θ 时, xn 发生的概率。这里的参数 θ 是一个向量(参数向量 θ=(θ1,θ2,...,θm) )。当然 θ 是可以变化(不断变化 θ 代表不同的概率密度分布函数,只是具有相同的类型),因此 θ 是参数向量集合的 Θ 的一个元素。
通常写成 p(xi;θ) ,如果写成 p(xi|θ) 也是可以的,不过为与条件概率 p(xi|θ) 进行区分,就写成 p(xi;θ) ,这样可读性更好,毕竟 θ 是一个参数,而不是一个随机变量。
最大似然法参数估计(Maximum Likehood Estimation MLE)
最大似然法(Maximum Likelihood)这种参数估计方法:它认为从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大,而不是像最小二乘估计法旨在得到使得模型能最好地拟合样本数据的参数估计量。
我们确实不得不佩服数学家的智慧,换个角度想问题,解决同样一个问题的方式就完全发生了改变。但是我们也还是要看到,这两种方法都还是有比较强的假设成份在里面,所以数学家往往也是敢于假设的。最大似然法其实来源于一个不算太严谨的假设,至少我个人是这样认为的,但是换句话说,如果用太严谨的假设,统计学也就没法玩了,所以在数理统计学面前,我们要不能太计较小概率事件,这和买彩票不一样,再夸张一点,有时候差不多就行了,哪怕这个事情发生的概率其实还真不是太小。回到最大似然法的就是,如果我们看到了一个系统给出了有限次的结果(组成一个结果集合ObserveSet),那么就说这个系统就具备这样的特性——如果再做重复实验的话,那么产生结果集合ObserveSet的概率最大。大家看到这里只能呵呵了。举个极端情况的例子,大家都比较喜欢看车模美女对吧?如果某次大家去看车展,心血来潮,想调查一下本次车模都可以打多少分,也就是车模颜值是如何分布的,所以就没有进去,就在门口盯着看,看车展完了之后走出来的美女然后给其打分,盯了半天你终于看到一个车模走了出来,不太漂亮,甚至比较丑,顶多59分,绝对达不到及格线,于是乎,你就判断本次车展不太行,这个系统产生的车模颜值不理想。政治老师或者语文老师一定会告诉我们犯了大错了——以偏概全,管中窥豹,盲人摸象等等,总之是不能这么推论。但是现实是残酷的,有时候我们就掌握这样不全的数据,却要从事一项伟大的事业,所以呢,幸好我们还有统计学老师和机器学习老师,告诉我们这样做是可以的,而且呢,如果不是这么极端的话,多一些样本,做出这样的估计就不会那么艰难,那么纠结。比如说,你等了两个多小时,这期间走出来20位模特,其中有12位不及格,40-59分之间,只有1位惊若天人,美得不可方物,其它的7位尚可。这时候你便可以心安理得的估计本次车展这个系统具有这样的参数( 参展商都是一些地方小公司,模特领到的报酬比较低),导致产生的模特颜值不高,美女凤毛麟角。我想大概齐这样估计是可以的,不管你认不认可,反正最大似然法是这样认为的——本次车展系统只有很小概率产生美女。
到现在为止,我是大概明白了似然的意思,其实是从英文likelihood翻译过来了,“似然似然”,似乎就是这样吧,“最大似然”,最大可能就是这样吧。
有了前面联合概率密度的基础,需要优化的目标函数就粉墨登场了(同样假设样本独立分布,估计参数
θ
)。
由于 xi 已知,所以需要改写成:
细心的朋友已经发现,函数已经定义成了 L 函数了,不再是
由于 L(θ) 是连乘,由于对数函数ln的单调性,实际应用中是两边求对数,即
并且为了简化运算,进一步定义:
最大似然函数 ln L(θ) :
最终估计的 θ 值:
接下来我们稍加思考,不难发现,最大似然函数参数估计求解的步骤:
(1)对 l^(θ)函数 求偏导,令各个偏导数为0,建立似然方程 。
(2)对似然方程进行求解,得到的参数即为所求估计值。
贝叶斯估计与最大后验估计(MAP)
上面提到的极大似然估计和贝叶斯估计分别代表了频率派和贝叶斯派的观点(看不懂没关系,直接往下接着看,回头再回味这句话更深刻)。
频率派认为,参数是客观存在的,只是未知而矣。因此,频率派最关心极大似然函数,只要参数
θˆMLE
求出来了,给定自变量
x
,
相反的,贝叶斯派认为参数也是随机的,和一般随机变量没有本质区别,正是因为参数不能固定,当给定一个输入
x
后,我们不能用一个确定的
现在,假设
θ
的先验分布为
g(θ)
,通过贝叶斯理论,对于
θ
的后验分布如下:
上面就是全贝叶斯估计,但是我们发现计算上面的后验概率 f(θ|X) ,通常是很难的,有一个积分项,难以找到典型的解析解,所以干脆就忽略分母的这个积分项,用一种近似的办法,就是将最大后验估计的目标为:
从结构上看,他和最大似然估计最大的不同在于, MAP多了一项先验分布,它体现了贝叶斯认为参数也是随机变量的观点,在实际运算中通常通过超参数给出先验分布。
怎么去理解这其中的差别呢?这里直接引用了
http://www.cnblogs.com/liliu/archive/2010/11/24/1886110.html 中的一个例子:
假设有五个袋子,各袋中都有无限量的饼干(樱桃口味或柠檬口味),已知五个袋子中两种口味的比例分别是
樱桃 100%樱桃 75% + 柠檬 25%
樱桃 50% + 柠檬 50%
樱桃 25% + 柠檬 75%
柠檬 100%
如果只有如上所述条件,那问从同一个袋子中连续拿到2个柠檬饼干,那么这个袋子最有可能是上述五个的哪一个?
我们首先采用最大似然估计来解这个问题,即上面描述中成功的概率p(拿到柠檬)的0,25%,50%,75%,1。我们只需要评估一下这五个值哪个值使得似然函数最大即可,得到为袋子5。这里便是最大似然估计的结果。
上述最大似然估计有一个问题,就是没有考虑到模型本身的概率分布,下面我们扩展这个饼干的问题。
假设拿到袋子1或5的机率都是0.1,拿到2或4的机率都是0.2,拿到3的机率是0.4,那同样上述问题的答案呢?这个时候就变MAP了。根据题意的描述可知,p的取值分别为0,25%,50%,75%,1,g的取值分别为0.1,0.2,0.4,0.2,0.1.分别计算出MAP函数的结果为:0,0.0125,0.125,0.28125,0.1.由上可知,通过MAP估计可得结果是从第4个袋子中取得的最高(其实这一点非常符合生活中的常识,虽然袋子5中的成功的概率是最高的,但是不一定容易拿到,所以还要综合一下拿到的容易程度)。
我自己再举一个比较俗的例子吧,比如说面前有机会,可以追的姑娘有三个,但是你只能追其中一个(对吧?),第一个长得好(0.9,当做 f=0.9 ),但是不好追(成功概率为0.1,当做 g=0.1 ),第二个长相中等(0.7),可能追得到几率(成功概率为0.5),第三个长得不太好(0.5),可能追得到的几率(成功概率为0.6),男同胞们大家会追那个?贝叶斯派应该会计算 f∗g :0.09,0.35,0.30,追第二个吧。频率派也许会想,反正我只能追一次,第一个吧。(以上纯粹瞎掰,非逻辑严格的数学故事,敬请批评指正)。
对于主题类的模型来说,
最大期望算法
最大期望算法(Exception Maximization Algorithm,后文简称EM算法)是一种启发式的迭代算法,用于实现用样本对含有隐变量的模型的参数做极大似然估计。已知的概率模型内部存在隐含的变量,导致了不能直接用极大似然法来估计参数,EM算法就是通过迭代逼近的方式用实际的值带入求解模型内部参数的算法。
EM思想本身还是很复杂的,一句两句还真的说不明白,可参考写的另一篇博客。
Gibbs采样
越往下写越感觉到为了完全整明白LDA,是不是要把整个统计学都要研究一遍?!但是学习还得继续。
采样(sampling)就是以一定的概率分布,取一些样本数据。为什么要干这事呢?用来构造多变量概率分布的随机样本,比如构造两个或多个变量的联合分布,求积分,期望,之所以用采样的方法,是因为积分,期望或者联合分布很难计算出来。
对很多贝叶斯推断问题来说,有时候后验分布过于复杂,使得积分没有显示结果,数值方法也很难应用;有时候需要计算多重积分(比如后验分布是多元分布时)。这些都会带来计算上的很大困难。这也是在很长的时期内,贝叶斯统计得不到快速发展的一个原因。1990年代MCMC(Markov Chain Monte Carlo ,马尔科夫链蒙特卡洛)计算方法引入到贝叶斯统计学之后,一举解决了这个计算的难题。可以说,近年来贝叶斯统计的蓬勃发展,特别是在各个学科的广泛应用和MCMC方法的使用有着极其密切的关系。
MCMC( Markov Chain Monte Carlo):对于给定的概率分布p(x),我们希望能有便捷的方式生成它对应的样本。由于Markov链能收敛到平稳分布【至于为什么请参考文献16】, 于是一个很的漂亮想法是:如果我们能构造一个转移矩阵为P的马氏链,使得该马氏链的平稳分布恰好是p(x), 那么我们从任何一个初始状态x0出发沿着马氏链转移, 得到一个转移序列 x0,x1,x2,⋯xn,xn+1⋯,, 如果马氏链在第n步已经收敛了,于是我们就得到了 π(x) 的样本xn,xn+1⋯。
这个绝妙的想法在1953年被 Metropolis想到了,为了研究粒子系统的平稳性质, Metropolis考虑了物理学中常见的波尔兹曼分布的采样问题,首次提出了基于马氏链的蒙特卡罗方法,即Metropolis算法,并在最早的计算机上编程实现。Metropolis 算法是首个普适的采样方法,并启发了一系列 MCMC方法,所以人们把它视为随机模拟技术腾飞的起点。 Metropolis的这篇论文被收录在《统计学中的重大突破》中, Metropolis算法也被遴选为二十世纪的十个最重要的算法之一。
LDA建模的过程
应该说掌握了上述概率相关的知识以后,不难理解下面:LDA模型中一篇文档生成的方式:
(1)从狄利克雷分布
α
中取样生成文档
i
的主题分布
(2)从主题的多项式分布
θi
中取样生成文档i第j个词的主题
zi,j
(3)从狄利克雷分布
β
中取样生成主题
zi,j
的词语分布
ϕzi,j
(4)从词语的多项式分布
ϕzi,j
中采样最终生成词语
wi,j
LDA建模算法
至此为之,我们要去考虑,怎么去计算这两个矩阵,怎么去优化的问题了。Spark采用的两种优化算法:
(1)EMLDAOptimizer 通过在likelihood函数上计算最大期望EM,提供较全面的结果。
(2)OnlineLDAOptimizer 通过在小批量数据上迭代采样实现online变分推断,比较节省内存。在线变分预测是一种训练LDA模型的技术,它以小批次增量式地处理数据。由于每次处理一小批数据,我们可以轻易地将其扩展应用到大数据集上。MLlib按照 Hoffman论文里最初提出的算法实现了一种在线变分学习算法。
LDA supports different inference algorithms via setOptimizer function. EMLDAOptimizer learns clustering using expectation-maximization on the likelihood function and yields comprehensive results, while OnlineLDAOptimizer uses iterative mini-batch sampling for online variational inference and is generally memory friendly.
Spark 代码分析、参数设置及结果评价
SPARK中可选参数
(1)K:主题数量(或者说聚簇中心数量)
(2)maxIterations:EM算法的最大迭代次数,设置足够大的迭代次数非常重要,前期的迭代返回一些无用的(极其相似的)话题,但是继续迭代多次后结果明显改善。我们注意到这对EM算法尤其有效。,至少需要设置20次的迭代,50-100次是更合理的设置,取决于你的数据集。
(3)docConcentration(Dirichlet分布的参数
α
):文档在主题上分布的先验参数(超参数
α
)。当前必须大于1,值越大,推断出的分布越平滑。默认为-1,自动设置。
(4)topicConcentration(Dirichlet分布的参数
β
):主题在单词上的先验分布参数。当前必须大于1,值越大,推断出的分布越平滑。默认为-1,自动设置。
(5)checkpointInterval:检查点间隔。maxIterations很大的时候,检查点可以帮助减少shuffle文件大小并且可以帮助故障恢复。
SPARK中模型的评估
(1)perplexity是一种信息理论的测量方法,b的perplexity值定义为基于b的熵的能量(b可以是一个概率分布,或者概率模型),通常用于概率模型的比较
LDA takes in a collection of documents as vectors of word counts and the following parameters (set using the builder pattern):
(1)k: Number of topics (i.e., cluster centers)
(2):optimizer: Optimizer to use for learning the LDA model, either EMLDAOptimizer or OnlineLDAOptimizer
(3)docConcentration: Dirichlet parameter for prior over documents’ distributions over topics. Larger values encourage smoother inferred distributions.
(4)topicConcentration: Dirichlet parameter for prior over topics’ distributions over terms (words). Larger values encourage smoother inferred distributions.
(5):maxIterations: Limit on the number of iterations. It is important to do enough iterations. In early iterations, EM often has useless topics, but those topics improve dramatically after more iterations. Using at least 20 and possibly 50-100 iterations is often reasonable, depending on your dataset.
(6)checkpointInterval: If using checkpointing (set in the Spark configuration), this parameter specifies the frequency with which checkpoints will be created. If maxIterations is large, using checkpointing can help reduce shuffle file sizes on disk and help with failure recovery.
All of spark.mllib’s LDA models support:
(1)describeTopics: Returns topics as arrays of most important terms and term weights
(2)topicsMatrix: Returns a vocabSize by k matrix where each column is a topic
详细代码注释
import org.apache.spark.sql.SparkSession
import org.apache.log4j.{Level, Logger}
import org.apache.spark.ml.clustering.LDA
object myClusters {
def main(args:Array[String]){
//屏蔽日志
Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)
val warehouseLocation = "/Java/Spark/spark-warehouse"
val spark=SparkSession
.builder()
.appName("myClusters")
.master("local[4]")
.config("spark.sql.warehouse.dir",warehouseLocation)
.getOrCreate();
val dataset_lpa=spark.read.format("libsvm")
.load("/spark-2.0.0-bin-hadoop2.6/data/mllib/sample_lda_libsvm_data.txt")
//------------------------------------1 模型训练-----------------------------------------
/**
* k: 主题数,或者聚类中心数
* DocConcentration:文章分布的超参数(Dirichlet分布的参数),必需>1.0,值越大,推断出的分布越平滑
* TopicConcentration:主题分布的超参数(Dirichlet分布的参数),必需>1.0,值越大,推断出的分布越平滑
* MaxIterations:迭代次数,需充分迭代,至少20次以上
* setSeed:随机种子
* CheckpointInterval:迭代计算时检查点的间隔
* Optimizer:优化计算方法,目前支持"em", "online" ,em方法更占内存,迭代次数多内存可能不够会抛出stack异常
*/
val lda=new LDA()
.setK(3)
.setTopicConcentration(3)
.setDocConcentration(3)
.setOptimizer("online")
.setCheckpointInterval(10)
.setMaxIter(100)
val model=lda.fit(dataset_lpa)
/**生成的model不仅存储了推断的主题,还包括模型的评价方法。*/
//---------------------------------2 模型评价-------------------------------------
//模型的评价指标:ogLikelihood,logPerplexity
//(1)根据训练集的模型分布计算的log likelihood,越大越好。
val ll = model.logLikelihood(dataset_lpa)
//(2)Perplexity评估,越小越好
val lp = model.logPerplexity(dataset_lpa)
println(s"The lower bound on the log likelihood of the entire corpus: $ll")
println(s"The upper bound bound on perplexity: $lp")
//---------------------------------3 模型及描述------------------------------
//模型通过describeTopics、topicsMatrix来描述
//(1)描述各个主题最终的前maxTermsPerTopic个词语(最重要的词向量)及其权重
val topics=model.describeTopics(maxTermsPerTopic=2)
println("The topics described by their top-weighted terms:")
topics.show(false)
/**主题 主题包含最重要的词语序号 各词语的权重
+-----+-------------+------------------------------------------+
|topic|termIndices |termWeights |
+-----+-------------+------------------------------------------+
|0 |[5, 4, 0, 1] |[0.21169509638828377, 0.19142090510443274]|
|1 |[5, 6, 1, 2] |[0.12521929515791688, 0.10175547561034966]|
|2 |[3, 10, 6, 9]|[0.19885345685860667, 0.18794498802657686]|
+-----+-------------+------------------------------------------+
*/
//(2) topicsMatrix: 主题-词分布,相当于phi。
val topicsMat=model.topicsMatrix
println("topicsMatrix")
println(topicsMat.toString())
/**topicsMatrix
12.992380082908886 0.5654447550856024 16.438154549631257
10.552480038361052 0.6367807085306598 19.81281695100224
2.204054885551135 0.597153999004713 6.979803589429554
*
*/
//-----------------------------------4 对语料的主题进行聚类---------------------
val topicsProb=model.transform(dataset_lpa)
topicsProb.select("label", "topicDistribution")show(false)
/** label是文档序号 文档中各主题的权重
+-----+--------------------------------------------------------------+
|label|topicDistribution |
+-----+--------------------------------------------------------------+
|0.0 |[0.523730754859981,0.006564444943344147,0.46970480019667477] |
|1.0 |[0.7825074858166653,0.011001204994496623,0.206491309188838] |
|2.0 |[0.2085069748527087,0.005698459472719417,0.785794565674572] |
...
*/
}
}
虽然推断出K个主题,进行聚类是LDA的首要任务,但是从代码第4部分输出的结果(每篇文章的topicDistribution,即每篇文章在主题上的分布)我们还是可以看出,LDA还可以有更多的用途:
(1)特征生成:LDA可以生成特征(即topicDistribution向量)供其他机器学习算法使用。如前所述,LDA为每一篇文章推断一个主题分布;K个主题即是K个数值特征。这些特征可以被用在像逻辑回归或者决策树这样的算法中用于预测任务。
(2)降维:每篇文章在主题上的分布提供了一个文章的简洁总结。在这个降维了的特征空间中进行文章比较,比在原始的词汇的特征空间中更有意义。
所以呢,我们需要记得LDA的多用途,(1)聚类,(2)降纬,(3)特征生成,一举多得,典型的多面手。
对参数进行调试
online 方法setMaxIter
//对迭代次数进行循环
for(i<-Array(5,10,20,40,60,120,200,500)){
val lda=new LDA()
.setK(3)
.setTopicConcentration(3)
.setDocConcentration(3)
.setOptimizer("online")
.setCheckpointInterval(10)
.setMaxIter(i)
val model=lda.fit(dataset_lpa)
val ll = model.logLikelihood(dataset_lpa)
val lp = model.logPerplexity(dataset_lpa)
println(s"$i $ll")
println(s"$i $lp")
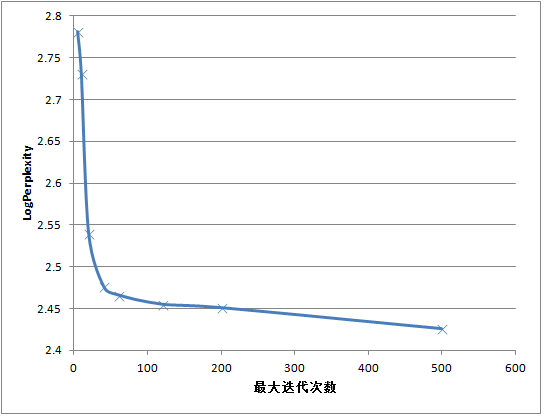
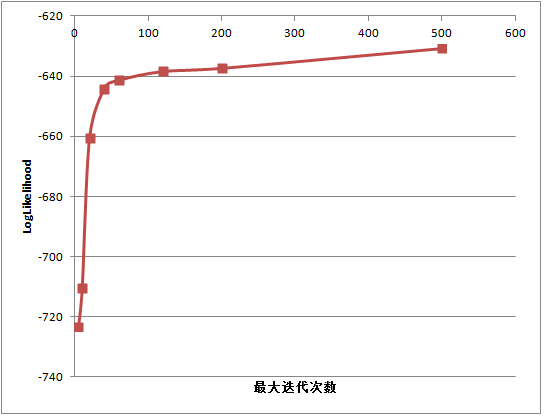
}可以得到如下的结果:logPerplexity在减小,LogLikelihood在增加,最大迭代次数需要设置50次以上,才能收敛:
Dirichlet分布的参数
α
、
β
docConcentration(Dirichlet分布的参数
α
)
topicConcentration(Dirichlet分布的参数
β
)
首先要强调的是EM和Online两种算法,上述两个参数的设置是完全不同的。
EM方法:
(1)docConcentration: 只支持对称先验,K维向量的值都相同,必须>1.0。向量-1表示默认,k维向量值为(50/k)+1。
(2)topicConcentration: 只支持对称先验,值必须>1.0。向量-1表示默认。
docConcentration: Only symmetric priors are supported, so all values in the provided k-dimensional vector must be identical. All values must also be >1.0. Providing Vector(-1) results in default behavior (uniform k dimensional vector with value (50/k)+1
topicConcentration: Only symmetric priors supported. Values must be >1.0. Providing -1 results in defaulting to a value of 0.1+1.
由于这些参数都有明确的设置规则,因此也就不存在调优的问题了,计算出一个固定的值就可以了。但是我们还是实验下:
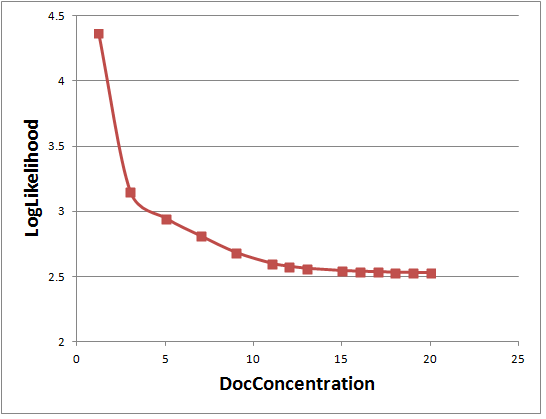
//EM 方法,分析setDocConcentration的影响,计算(50/k)+1=50/5+1=11
for(i<-Array(1.2,3,5,7,9,11,12,13,14,15,16,17,18,19,20)){
val lda=new LDA()
.setK(5)
.setTopicConcentration(1.1)
.setDocConcentration(i)
.setOptimizer("em")
.setMaxIter(30)
val model=lda.fit(dataset_lpa)
val lp = model.logPerplexity(dataset_lpa)
println(s"$i $lp")
}可以看出果然DocConcentration>=11后,logPerplexity就不再下降了。
在确定DocConcentration=11后,继续对topicConcentration分析,发现logPerplexity对topicConcentration不敏感。
1.1 2.602768469
1.2 2.551084142
1.5 2.523405179
2.0 2.524881353
5 2.575868552
Online Variational Bayes
(1)docConcentration: 可以通过传递一个k维等价于Dirichlet参数的向量作为非对称先验。值应该>=0。向量-1表示默认,k维向量值取(1.0/k)。
(2)topicConcentration: 只支持对称先验。值必须>=0。-1表示默认,取值为(1.0/k)。
docConcentration: Asymmetric priors can be used by passing in a vector with values equal to the Dirichlet parameter in each of the k dimensions. Values should be >=0>=0. Providing Vector(-1) results in default behavior (uniform k dimensional vector with value (1.0/k)(1.0/k))
topicConcentration: Only symmetric priors supported. Values must be >=0>=0. Providing -1 results in defaulting to a value of (1.0/k)(1.0/k).
运行LDA的小技巧
(1)确保迭代次数足够多。这个前面已经讲过了。前期的迭代返回一些无用的(极其相似的)话题,但是继续迭代多次后结果明显改善。我们注意到这对EM算法尤其有效。
(2)对于数据中特殊停用词的处理方法,通常的做法是运行一遍LDA,观察各个话题,挑出各个话题中的停用词,把他们滤除,再运行一遍LDA。
(3)确定话题的个数是一门艺术。有些算法可以自动选择话题个数,但是领域知识对得到好的结果至关重要。
(4)特征变换类的Pipeline API对于LDA的文字预处理工作极其有用;重点查看Tokenizer,StopwordsRemover和CountVectorizer接口.
对文本的预处理,还可以参考我的另外两篇文章《Spark2.0 特征提取、转换、选择之一:数据规范化…》《Spark2.0 特征提取、转换、选择之二:特征选择、文本处理…》。
参考文献:
(1)Spark document
(2) zouxy09的CSDN 从最大似然到EM算法浅解
http://blog.csdn.net/zouxy09/article/details/8537620/
(3)4 步理解主题模型LDA http://www.tuicool.com/articles/reaIra6
(4)LDA主题模型与推荐系统 http://www.jianshu.com/p/50295398d802
(5)主题模型-LDA浅析 huagong_adu的CSDN博客
http://blog.csdn.net/huagong_adu/article/details/7937616/
(6)大规模主题模型:对Spark LDA算法的改进
http://www.csdn.net/article/2015-11-02/2826097
(7)Spark LDA pirage的CSDN博客
http://blog.csdn.net/pirage/article/details/50219323
(8)一篇非常简洁的但是清晰明了的概念主题模型简记
http://www.aichengxu.com/view/680260
(9) LDA主题模型评估方法–Perplexity
http://blog.csdn.net/pirage/article/details/9368535
(10) Spark MLlib LDA 源码解析
http://blog.csdn.net/sunbow0/article/details/47662603
(11)《模式识别》 希腊Sergios Theodoridis等著
(12)数据挖掘经典算法——最大期望算法http://www.cnblogs.com/yahokuma/p/3794905.html
(13)极大似然估计和贝叶斯估计 http://blog.sciencenet.cn/blog-520608-703219.html
(14)最大似然估计(MLE)和最大后验概率(MAP)http://www.cnblogs.com/liliu/archive/2010/11/24/1886110.html
(15)自然语言处理之LDA http://www.tuicool.com/articles/nQR3Yzf
(16)MCMC(Markov Chain Monte Carlo) and Gibbs Sampling http://www.cnblogs.com/ywl925/archive/2013/06/05/3118875.html
























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








