支持向量机学习之3-SVR（回归）

支持向量机系列学习笔记包括以下几篇：
Spark机器学习系列之13： 支持向量机SVM ：http://blog.csdn.net/qq_34531825/article/details/52881804
支持向量机学习之2：核函数http://blog.csdn.net/qq_34531825/article/details/52895621
支持向量机学习之3：SVR（回归）http://blog.csdn.net/qq_34531825/article/details/52891780

$\epsilon-SVR$

SVR回归中，基本思路和SVM中是一样的，在$\epsilon-SVR$[Vapnic,1995] 需要解决如下的优化问题。

$$min \ \ \frac{1}{2}||w||^2+C\sum_{i=1}^{l}(\xi_i+\xi^*_i)$$ $$s.t. \ \ \left\{ \begin{aligned} &y_i-(w^Tx_i+b)<\epsilon+\xi_i \\ &(w^Tx_i+b)-y_i<\epsilon+\xi^*_i \\ &\xi_i,\xi^*_i\geq 0 \\ \end{aligned} \right.$$
细心的读者可能已经发现了与 $C-SVM$中的具有相似的地方，但又不太一样，那么如何理解上述公式呢？
假设我们的训练数据集是 $\{(x_1,y_1),(x_2,y_2),...(x_n,y_l)\}$
我们的目标是找到一个函数，比如线性函数 $f(x)=w^Tx+b$,使得
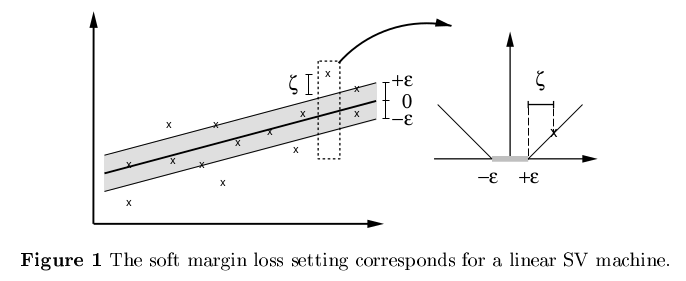
如果数据离回归函数的偏差 $|y_i-w^Tx-b|<\epsilon|$(下图非色区域）,我们是能接受的，不需要付出任何代价（即不需要在代价函数中体现）。我们只关注偏差大于 $\epsilon$的代价。举个例子来说，就好比我们在换外币时，我们并不关注少量 $\epsilon$损失，这部分损失是汇率引起的合理损失。
所以约束条件是保证更多多的数据点都在灰色范围内（拟合最佳的线性回归函数，使得更多的点落在我们接受的精度范围内），即 $|y_i-w^Tx-b|<\epsilon|$。但是我们发现，还是会有一部分点，偏差比较大，落在灰色区域之外，所以类似SVM中使用的方法，引入松弛因子，采取软边界的方法，而且上下采取不同的松弛因子 $\xi_i,\xi^*_i\geq 0$，这样就不难得出约束条件为：
$$s.t. \ \ \left\{ \begin{aligned} &y_i-(w^Tx_i+b)<\epsilon+\xi_i \\ &(w^Tx_i+b)-y_i<\epsilon+\xi^*_i \\ &\xi_i,\xi^*_i\geq 0 \\ \end{aligned} \right.$$

如同SVM中一样的，在多数情况下转换为对偶问题更容易计算。同时还可以计算出 $w$和$b$，直接看文献1吧。



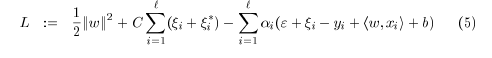
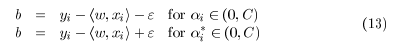
详细推导过程看文献1。

使用核函数的$\epsilon-SVR$

文献2

$\nu-SVR$

Chang and Lin (2002) prove that $\epsilon$-SVR with parameters $( \overline C̄,\epsilon)$has the same solution as $\nu$-SVR with parameters$(l\overline C̄,\nu)$.
其实两种SVR在满足一定条件下，具有相同的解。

优缺点分析

Scikit代码

#-*-coding:utf-8-*- 
import numpy as np  
from sklearn.svm import SVR  
import matplotlib.pyplot as plt  

###############################################################################  
# Generate sample data  
X = np.sort(5 * np.random.rand(40, 1), axis=0)  #产生40组数据，每组一个数据，axis=0决定按列排列，=1表示行排列  
y = np.sin(X).ravel()   #np.sin()输出的是列，和X对应，ravel表示转换成行  

###############################################################################  
# Add noise to targets  
y[::5] += 3 * (0.5 - np.random.rand(8))  

###############################################################################  
# Fit regression model  
svr_rbf10 = SVR(kernel='rbf',C=100, gamma=10.0)  
svr_rbf1 = SVR(kernel='rbf', C=100, gamma=0.1)  
svr_rbf1 = SVR(kernel='rbf', C=100, gamma=0.1)  
#svr_lin = SVR(kernel='linear', C=1e3)  
#svr_poly = SVR(kernel='poly', C=1e3, degree=3)  
y_rbf10 = svr_rbf10.fit(X, y).predict(X)  
y_rbf1 = svr_rbf1.fit(X, y).predict(X) 
#y_lin = svr_lin.fit(X, y).predict(X)  
#y_poly = svr_poly.fit(X, y).predict(X)  

###############################################################################  
# look at the results  
lw = 2 #line width  
plt.scatter(X, y, color='darkorange', label='data')  
plt.hold('on')  
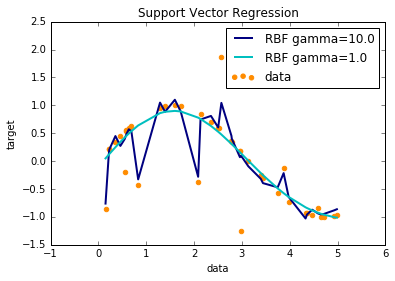
plt.plot(X, y_rbf10, color='navy', lw=lw, label='RBF gamma=10.0')  
plt.plot(X, y_rbf1, color='c', lw=lw, label='RBF gamma=1.0')  
#plt.plot(X, y_lin, color='c', lw=lw, label='Linear model')  
#plt.plot(X, y_poly, color='cornflowerblue', lw=lw, label='Polynomial model')  
plt.xlabel('data')  
plt.ylabel('target')  
plt.title('Support Vector Regression')  
plt.legend()  
plt.show()

RBF不同参数：

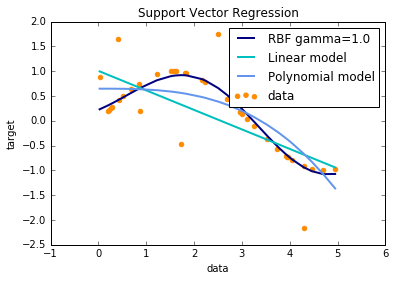
不同核函数：

主要参考文献
（1）A Tutorial on Support Vector Regression ,Alex J
http://www.svms.org/regression/SmSc98.pdf
（2）LIBSVM:A library for Support Vector-Machines Chih-Chung Chang and Chih-Jen Lin
（3）支持向量机回归算法研究 硕士学位论文