支持向量机学习之2：核函数

支持向量机系列学习笔记包括以下几篇：
Spark机器学习系列之13： 支持向量机SVM ：http://blog.csdn.net/qq_34531825/article/details/52881804
支持向量机学习之2：核函数http://blog.csdn.net/qq_34531825/article/details/52895621
支持向量机学习之3：SVR（回归）http://blog.csdn.net/qq_34531825/article/details/52891780

本文绝大部分内容转载自 http://blog.csdn.net/xiaojiegege123456/article/details/7728198，xiaojiegege123456 CSDN，在我读完参考文献2，3之后，对原文有微细的增改。
SVM最终要转换为对偶问题如下：

$$max \quad\quad\quad\quad W(\alpha)=\sum\limits_{i=1}^{n}{\alpha_i}-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j<x_i,x_j>}$$
$$s.t. \left\{ \begin{aligned} \quad\quad\quad\quad \sum\limits_{i=1}^{n}{\alpha_iy_i}=0 \\ \alpha_i \geq 0 \quad\quad\quad\quad i=1...n\\ \end{aligned} \right.$$
的求解需要计算 <xi,xj> <script type="math/tex" id="MathJax-Element-3"> </script>这个内积，而如果输入样本线性不可分的话，我们采取的方法是通过 $\Phi:X\mapsto F$函数映射将输入样本映射到另外一个高维空间并使其线性可分。

以库克定律为例(http://zh.wikipedia.org/zh-cn/%E9%9D%99%E7%94%B5%E5%8A%9B)：
一个电量为 $q'\,\!$ 的点电荷作用于另一个电量为 $q\,\!$ 的点电荷，其静电力 $F\,\!$ 的大小，可以用方程表达为:

$$F = k_{\mathrm{e}}\frac{qq'}{r^2}\,\!$$ 其中， $r\,\!$ 是两个点电荷之间的距离， $k_{\mathrm{e}}\,\!$ 是库仑常数。
显然这个定律无法用线性学习器来表达，看到乘积想到ln函数，对原始形式两边取ln，得到： $$lnF(q,q^{'},r)=ln(k_e)+ln(q)+ln(q^{'})-2ln(r) >$$ ，令 $x_2=ln(q)，x_3=ln(q^{'})，x_4=ln(r)，x_1=in(k_e)，G(\vec{x})=ln(F(q,q^{'},r))$，那么就得到一个线性学习器：
$G(\vec{x})=x_1+x_2+x_3-2x_4=w^T\vec{x},其中\vec{x}=[x_1,x_2,x_3,x_4]^T$
这个过程可以用下图说明：

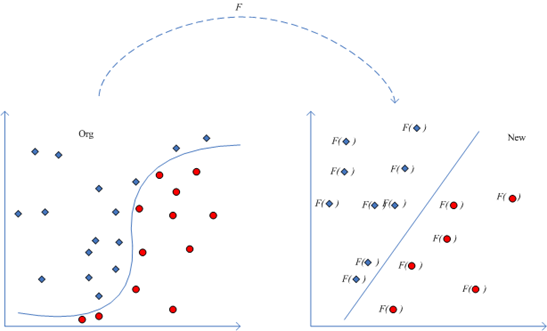
考虑映射$\Phi$,将一个低维空间的特征如$\Re^2$空间$（x_1,x_2)$映射为$\Re^3$空间$（x_1^2,\sqrt2x_1x_2,x_2^2)$,这样也许原来不可分的数据在高维度空间就变得可分了。

完成映射之后，原来需要计算 <xi,xj> <script type="math/tex" id="MathJax-Element-19"> </script>,现在需要计算 <Φ(xi),Φ(xj)> <script type="math/tex" id="MathJax-Element-20"><\Phi(x_i),\Phi(x_j)></script>:

$$max \quad\quad\quad\quad W(\alpha)=\sum\limits_{i=1}^{n}{\alpha_i}-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j<\Phi(x_i),\Phi(x_j)>}$$

但是随之而来的问题是，维度增加意味着特征个数增加，SVM中需要增加$\alpha_i$的个数，复杂度提高了，从而导致模型的泛化能力(学习器对训练样本以外数据的适应性)会随着维度的增长而大大降低，这也违反了“奥坎姆的剃刀”(这个原理称为“如无必要，勿增实体”，即“简单有效原理”。)
也许看到这里会觉得从$\Phi :\Re^2\mapsto \Re^3$有什么呀，不就多一个特征吗？其实上面是最简单的一个特殊例子，一般来说，如果我们把一个维度为$d$的低维度空间特征映射到高维度空间，假设映射后单项式的次数为$p$（如三个单项式$x_1^2,\sqrt2x_1x_2,x_2^2,p都为2$）,那么通过可以组合出$\binom{d+p-1}{p}$个特征，呵呵，现在感觉到害怕了吧？！这个数能达到多少呢？Vapnik等人举了个例子，对于表现较好的OCR识别来说，$p=7,d=28*28=784,相应大约组合出3.7*10^{16}个特征$。
因此想要：先找到这种映射，然后将输入空间中的样本映射到新的空间中，最后在新空间中去求内积 <Φ(xi),Φ(xj)> <script type="math/tex" id="MathJax-Element-29"><\Phi(x_i),\Phi(x_j)></script>是绝对不可行的。
因此我们需要找到某种方法，它不需要显式的将输入空间中的样本映射到新的空间中而能够在输入空间中直接计算出内积 <Φ(xi),Φ(xj)> <script type="math/tex" id="MathJax-Element-30"><\Phi(x_i),\Phi(x_j)></script>。核函数就这样被研究出来了。再调强以下，它是对输入空间向高维空间的一种隐式映射，它不需要显式的给出那个映射，在输入空间就可以计算 <Φ(xi),Φ(xj)> <script type="math/tex" id="MathJax-Element-31"><\Phi(x_i),\Phi(x_j)></script>：
定义1:核是一个函数$K$，对于所有的$x,x^{'} \in X$满足，$K<x,x^{'} >=<\Phi(x),\Phi(x^{'} )>$ ，这里的$\Phi$为从$X$到内积特征空间$F$的映射。
于是输入空间的标准内积就被推广了。
对于前面提到的：映射$\Phi$,将一个低维空间的特征如$\Re^2$空间$x=（x_1,x_2)$映射为$\Re^3$空间$(x_1^2,\sqrt2x_1x_2,x_2^2)$,
可以证明：

<(x21,2√x1x2,x22),(x′21,2√x′1x′2,x′22)>=<x,x′>2

<script type="math/tex; mode=display" id="MathJax-Element-43"><(x_1^2,\sqrt2x_1x_2,x_2^2),({x^{'}}_1^2,\sqrt2{x^{'}}_1{x^{'}}_2,{x^{'}}_2^2)>= ^2</script>
所以就找了 $K(x,x^{'})=<x,x^{'}>^2$,是不是输入空间的标准内积 <x,x′) <script type="math/tex" id="MathJax-Element-45"> 上面是一个特殊的例子，那么一般核函数K(x,y)通过什么样的方法去寻找呢？
假设有输入空间 $X={x_1,x_2,....x_n}$且 $K(x,y)$为对称函数，那么对于所有样本得到下面矩阵： $k=(K(x_i,x_j))\quad\quad(i,j=0,...n)$，显然，这个是个对称矩阵，那么对于对称矩阵一定存在一个正交矩阵，使得 $P^TkP=\Lambda$，这里 $\Lambda$是包含 $k$的特征值$\lambda_i$的对角矩阵，特征值 $\lambda_i$对应的特征向量为 $v_t=(v_{t1},v_{t2},...v_{tn})^T$，其中 $n$为样本数，对输入空间做如下映射$\phi$：
$\phi:x_i|->(\sqrt{\lambda_1}v_{1i},\sqrt{\lambda_2}v_{2i}...\sqrt{\lambda_n}v_{tn})\quad\quad \in R^n(i=1,...n)$
于是有 <ϕ(xi),ϕ(xj)>=∑t=1nλtvtivtj=(VΛVT)i,j=ki,j=K(xi,xj) <script type="math/tex" id="MathJax-Element-58"><\phi(x_i),\phi(x_j)>=\sum\limits_{t=1}^n{\lambda_tv_{ti}v_{tj}}=(V\Lambda V^T)_{i,j}=k_{i,j}=K(x_i,x_j)</script>，( $其中V为特征向量组成的矩阵，\Lambda为相应特征值组成的三角矩阵)，也就是说K是对应于映射\phi的核函数$。

例子：

$$k= \left[ \begin{array}{cccc} 4&0&0\\ 0&3&1\\ 0&1&3\\ \end{array}\right ]$$ ，其特征向量： $v_1=(1,0,0)^T和v_2=(0,\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T，v_3=(0,-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})^T，V=(v_1,v_2,v_3)= \left[ \begin{array}{cccc} 1&0&0\\ 0&\frac{1}{\sqrt(2)}&-\frac{1}{\sqrt(2)}\\ 0&\frac{1}{\sqrt(2)}&\frac{1}{\sqrt(2)}\\ \end{array}\right ]，满足V^{-1}kV=\Lambda=\left[ \begin{array}{cccc} 4&0&0\\ 0&4&0\\ 0&0&2\\ \end{array}\right ]，对所有输入样本做映射得：$>
$\phi(x_1)=(\sqrt{4}*1,\sqrt{4}*0,\sqrt{2}*0)=(2,0,0)^T$；>
$\phi(x_2)=(\sqrt{4}*0,\sqrt{4}*\frac{1}{\sqrt{2}},\sqrt{2}*(-\frac{1}{\sqrt{2}}))^T=(0,\sqrt{2},-1)$;
$\phi(x_3)=(\sqrt{4}*0,\sqrt{4}*\frac{1}{\sqrt{2}},\sqrt{2}*\frac{1}{\sqrt{2}})^T=(0,\sqrt{2},1)$。
随便选两个做内积，如 <ϕ(x2),ϕ(x3)>=0∗0+2√∗2√+(−1)∗1=1=K(x2,x3) <script type="math/tex" id="MathJax-Element-65"><\phi(x_2),\phi(x_3)>=0*0+\sqrt{2}*\sqrt{2}+(-1)*1=1=K(x_2,x_3)</script>。
由此可见：K(x,y)就是对应于特征映射 $\phi$的核函数，

可以得到下面的结论：
定理1：存在有限输入空间$X，K(x,y)为X$上的对称函数，那么$K(x,y)$是核函数的充要条件是矩阵$k=(K(x_i,x_j))\quad\quad(i,j=0,...n)$半正定，此时相当于对输入空间向特征空间进行了隐式的$\phi$映射。
对于上面的映射$\phi，令\phi_i(x_j)=\sqrt{\lambda_i}v_{ij}，$
于是$\phi(x)=(\phi_1(x),\phi_2(x),...\phi_n(x))$，

$进而K(x,y)=\sum\limits_{i=1}^\infty{\lambda_i\phi_i(x)\phi_i(y)}$。

定理3：设$X$是$R^n$的一个紧子集(闭合且有界子集)，$K(x,y)$为$X$上的对称函数，如果它在希尔伯特空间上的积分算子$T_kf(x)=f(t)dt$满足：$\forall{f} \in L_2(X),\quad \quad \quad \int_{X \times X}{K(x,y)f(x)f(y)dxdy} \geq 0$

这里$L_2$指的是由满足条件$\int f(x)^2dx< \infty$的所有函数f(x)组成的空间。

$在X \times X上扩展K(x,y)到一个一致收敛的序列，该序列由T_k的特征函数\phi_j \in L_2(x)构成，归一化使得||\phi_j||_{L_2}=1，且所有特征值\lambda_j \geq 0 ，则核函数K(x,y)可以被特征分解$为： $K(x,y)=\sum\limits_{i=1}^\infty{\lambda_i\phi_i(x)\phi_i(y)}$
定义2：设H是希尔伯特函数空间，其元素是某个抽象集合X上的实值或复值函数，如果对于任何$y \in X，K(x,y)$作为x的函数都是H中的元素，而且对于任何y \in X及f \in H取内积有：$f(y)=<f(x),K(x,y)>$
则H称为为再生核希尔伯特空间(Reproducing Kernel Hilbert Space，RKHS)；称$K(x,y)$为再生核空间H的再生核(简称RK)。
定理4：对于定义在域$X \subset R^d$上的每一个Mercer核$K(x,y)$，存在一个定义在X上的函数的再生希尔伯特空间RKHS，其中K是再生核。反过来，对于线性有界函数的任意希尔伯特空间，存在再生核这个命题也成立。
当然也可以利用核函数来构造核函数，有时候这种构造会很有效的解决问题：
条件：设$K_1(x,y)、K_2(x,y)是X \times X$上的核，$X \subseteq R^n，f$是X上的实值函数，$\phi:X->R^m，K_3(x,y)$是$R^m \times R^m$上的核，$A$是一个对称半正定矩阵，则下面的函数都是核：

$$1、K(x,y)=K_1(x,y)+K_2(x,y);\\ 2、K(x,y)=\alpha K_1(x,y);\\ 3、K(x,y)=K_1(x,y)K_2(x,y);\\ 4、K(x,y)=f(x)f(y);\\ 5、K(x,y)=K_3(\phi(x),\phi(y));\\ 6、K(x,y)=x^TAy。\\$$
核的选择对于支持向量机至关重要，选定核K(x_i,x_j)后，原问题就变成了：

$$max \quad \quad \quad \sum\limits_{i=1}^{n} \alpha_i-\frac{1}{2}\sum\limits_{i,j=1}^{n}y_iy_j\alpha_i\alpha_jK(x_i,x_j)$$ $$s.t.\quad\quad\quad\quad \sum\limits_{i=1}^{n}{\alpha_iy_i}=0$$ $$\alpha_i \geq 0 \quad\quad\quad\quad i=1...n$$

这个优化问题有最优解么？记得核要满足Mercer条件，即矩阵$k=(K(x_i,x_j))\quad\quad(i,j=0,...n)$在所有训练集上半正定，这说明这个优化是凸优化，于是这个条件保证了最大化间隔优化问题有唯一解，简直是天作之合啊，配合的天衣无缝；最后求的$(\alpha^*)$和b，那么从输入空间向特征空间隐式映射后得到的最大间隔超平面也就出来了：$f(x)=\sum\limits_{i=1}^{n}\alpha^*y_iK(x_i,x)+b^*，且有几何间隔\gamma=\frac{1}{||w^*||}= {(\sum\limits_{i \in support \quad vector}\alpha^*_i)}^{1/2}$。
常用核函数总结如下：
线性核函数：$K<x,y>=<x,y>^d$
多项式核函数：$K(x,y)=(<x,y>+1)^d$
高斯核函数：$K(x,y)=e^{\frac{-||x-y||^2}{2\delta^2}}$
Sigmoid核函数：$K(x,y)=tanh(\rho <x,y>+c)$
下面这个链接收集了若干核函数：
http://www.shamoxia.com/html/y2010/2292.html
关于核方法的理论部分涉及到泛函分析、微积分等等，水比较深，我推荐一本书：《Kernel Methods for Pattern Analysis》(模式分析的核方法)，作者是：John Shawe-Taylor和Nello Cristianini 。

主要参考文献
（1）http://blog.csdn.net/xiaojiegege123456/article/details/7728198，xiaojiegege123456 CSDN
（2）支持向量机通俗导论（理解SVM的三层境界） http://blog.csdn.net/v_july_v/article/details/7624837
（3）A Tutorial on Support Vector Regression， Alex J. Smola and Bernhard Scholkopf