机器学习笔记之条件随机场(一)背景介绍

引言

从本节开始，将介绍条件随机场。本节将从分类模型开始，引出条件随机场的模型性质。

回顾：线性分类

在感知机算法中，第一次介绍线性分类的类型：

硬分类算法(Hard Classification)

硬分类的核心思想是：线性模型在激活函数的映射结果$y_{pred}^{(i)}$的特征空间与真实标签结果$y^{(i)}$ 的特征空间相同。以二分类为例，数学符号表示如下：

• 已知数据集合$\mathcal{X}$,以及对应的真实标签集合$\mathcal{Y}$表示如下：
  $$\mathcal{X}={\left(\begin{array}{c}{x}_1^{(1)},x_2^{(1)},\cdots ,x_p^{(1)}\\ x_1^{(2)},x_2^{(2)},\cdots ,x_p^{(2)}\\ ⋮\\ x_1^{(N)},x_2^{(N)},\cdots ,x_p^{(N)}\end{array}\right)}_{N\times p}\mathcal{Y}={\left(\begin{array}{c}{y}^{(1)}\\ y^{(2)}\\ ⋮\\ y^{(N)}\end{array}\right)}_{N\times 1}$$
• 基于二分类，真实标签结果$y^{(i)}(i=1,2,\cdots ,N)$仅包含$2$个具体结果：
  这里用-1,1两个数字分类信息。
  y ( i ) ∈ { − 1 , 1 } ( i = 1 , 2 , ⋯   , N ) y^{(i)} \in \{-1,1\} \quad (i=1,2,\cdots,N) y(i)∈{−1,1}(i=1,2,⋯,N)
• 硬分类中模型通过样本，对于标签的预测结果$y_{pred}^{(i)}$与$y^{(i)}$的特征空间 相同：
  y p r e d ( i ) , y ( i ) ∈ { − 1 , 1 } ( i = 1 , 2 , ⋯   , N ) y_{pred}^{(i)},y^{(i)} \in \{-1,1\} \quad (i = 1,2,\cdots,N) ypred(i)​,y(i)∈{−1,1}(i=1,2,⋯,N)
• 在线性分类中，$y_{pred}^{(i)}$的拟合方程(模型)表示如下：
  $$y_{pred}^{(i)}=sign({\mathcal{W}}^T{x}^{(i)}+b)$$
  其中$sign$函数表示激活函数(Activation Function)，在硬分类中，激活函数通常以分段函数的形式表现出来：
  $k$表示某‘具体阈值’。
  $$sign(a)=\{\begin{array}{l}1ifa\ge k\\ -1else\end{array}$$

满足这种条件的模型，其代表有：
这里仅例举介绍过的模型。

• 线性判别分析(Linear Discriminant Analysis,LDA)
• 感知机算法(Perceptron Algorithm,PLA)
• 支持向量机(Support Vector Machine,SVM)

软分类算法(Soft Classification)

相对于硬分类算法直接比较预测标签与真实标签是否相同，软分类算法的核心思想是：其预测结果并非标签结果，而是概率结果，通过比较不同标签后验概率的大小关系来判定分类类别。

依然以二分类为例，已知某样本$x^{(i)}$，该样本条件下关于对应预测标签$y_{pred}^{(i)}$分别是$-1,1$的后验概率表示如下：
$$\mathcal{P}\left(y_{pred}^{(i)}=-1\mid x^{(i)}\right),\mathcal{P}\left(y_{pred}^{(i)}=1\mid x^{(i)}\right)$$
软分类思想数学符号表示如下：
$$\{\begin{array}{l}{y}_{pred}^{(i)}=-1if\mathcal{P}\left(y_{pred}^{(i)}=-1\mid x^{(i)}\right)\ge \mathcal{P}\left(y_{pred}^{(i)}=1\mid x^{(i)}\right)\\ y_{pred}^{(i)}=1else\end{array}$$

基于不同分类后验的比较思想，软分类思想分别衍生出两种模型：概率判别模型、概率生成模型。

本次针对概率判别模型、概率生成模型的思想描述相比于高斯判别分析(Gaussian Discriminant Analysis)中的描述更加泛化。

概率判别模型

概率判别模型(Probability Discriminant Model)的思想体现在：概率判别模型考虑的是条件概率分布之间的大小关系：

仍然以二分类为例：
$$\mathcal{P}\left(y_{pred}^{(i)}=-1\mid x^{(i)}\right)\stackrel{\text{?}}{\leftrightarrow }\mathcal{P}\left(y_{pred}^{(i)}=1\mid x^{(i)}\right)$$
基于该思想的典型模型是逻辑回归(Logistic Regression)。逻辑回归的特点在于直接将条件概率结果求解出来，并进行比较。逻辑回归使用连续激活函数描述样本点$x^{(i)}$与条件概率$\mathcal{P}(y_{pred}^{(i)})$之间的关系：
‘逻辑回归’只是二分类的判别方式，而基于多分类的判别方式被称为softmax Regression。
$$\begin{array}{rl}\mathcal{P}(y_{pred}^{(i)}\mid x^{(i)})& =sigmoid({\mathcal{W}}^T{x}^{(i)}+b)\\ & =\frac{1}{1+e^{-\left({\mathcal{W}}^T{x}^{(i)}+b\right)}}\end{array}$$
对应两种条件概率结果表示如下：
$$\{\begin{array}{l}\mathcal{P}(y_{pred}^{(i)}=1\mid x^{(i)})=\frac{1}{1+e^{-\left({\mathcal{W}}^T{x}^{(i)}+b\right)}}\\ \mathcal{P}(y_{pred}^{(i)}=-1\mid x^{(i)})=1-\frac{1}{1+e^{-\left({\mathcal{W}}^T{x}^{(i)}+b\right)}}=\frac{e^{-\left({\mathcal{W}}^T{x}^{(i)}+b\right)}}{1+e^{-\left({\mathcal{W}}^T{x}^{(i)}+b\right)}}\end{array}$$
最终通过求解模型参数$\mathcal{W},b$来确定条件概率之间的大小关系。

在最大熵原理与softmax激活函数关系中介绍过，sigmoid函数，softmax函数它不仅仅是激活函数，并且它们均是指数族分布，并且这两种分布是满足对应条件下熵最大的分布：

基于数据集合$\mathcal{X}$中各样本特征使用经验概率分布(Empirical Probability Distribution)；
经验概率分布是表达‘给定已知事实’的形式。对已知数据通过‘统计’的方式表示概率分布结果。
其中$x_i$表示数据的$k$种离散表示，可以看成$k$种离散的标签结果，而标签对应的概率表示如下：
$$\hat{P}(x^{(j)}=x_i)=\frac{count(x_i)}{N}\{\begin{array}{l}{x}^{(i)}\in \mathcal{X}\\ i=1,2,\cdots ,k\end{array}$$
其中sigmoid函数表示的$k=2$，而softmax表示$k\ge 2$，sigmoid函数是softmax函数在二分类下的特殊表示：
$$\begin{array}{rl}sigmoid(x)& =\frac{1}{1+e^{-x}}\\ & =\frac{e^0}{e^0+e^{-x}}\end{array}$$

因此，同样可以从 最大熵模型 的角度去理解逻辑回归模型。

概率生成模型

相比于概率判别模型，概率生成模型(Probability Generation Model)的思想体现在：并不直接针对条件概率进行求解，而是通过联合概率分布的大小关系来表示条件概率的大小关系。
其中$\mathcal{P}(x^{(i)})$是关于$x^{(i)}$的边缘概率分布。和$y_{pred}^{(i)}$无关，可视作常数。

依然以二分类为例，使用条件概率公式将$\mathcal{P}(y_{pred}^{(i)}=1\mid x^{(i)})$展开成如下形式：
$$\begin{array}{rl}\mathcal{P}(y_{pred}^{(i)}=1\mid x^{(i)})& =\frac{\mathcal{P}(y_{pred}^{(i)}=1,x^{(i)})}{\mathcal{P}(x^{(i)})}\\ & \propto \mathcal{P}(y_{pred}^{(i)}=1,x^{(i)})\\ & =\mathcal{P}(y_{pred}^{(i)}=1\mid x^{(i)})\cdot \mathcal{P}(x^{(i)})\end{array}$$
最终通过比较$\mathcal{P}(y_{pred}^{(i)}=1,x^{(i)})$和$\mathcal{P}(y_{pred}^{(i)}=-1,x^{(i)})$之间的大小关系来描述条件概率的大小关系：
$$\begin{gathered} \mathcal{P}(y_{pred}^{(i)}=1\mid x^{(i)})\stackrel{\text{?}}{\iff }\mathcal{P}(y_{pred}^{(i)}=-1\mid x^{(i)}) \\ \Downarrow \\ \mathcal{P}(x^{(i)},y_{pred}^{(i)}=1)\stackrel{\text{?}}{\iff }\mathcal{P}(x^{(i)},y_{pred}^{(i)}=-1) \end{gathered}$$

从宏观角度观察，未知变量的后验概率有时可能很难求解，因而需要使用推断(Inference)：通过已知变量推测未知变量的条件概率分布。
说远了~
常见的概率生成模型，如概率图模型系列：

• 朴素贝叶斯(Naive Bayes)
• 隐马尔可夫模型(Hidden Markov Model)
• 高斯混合模型(Gaussian Mixture Model)

最大熵马尔可夫模型

隐马尔可夫模型的缺陷

首先，隐马尔可夫模型本身是概率生成模型。在介绍隐马尔可夫模型的解码问题时，并没有对单一隐变量的后验概率进行求解，而是通过维特比算法(Viterbi)找出关于隐变量 联合概率分布之间的关联关系，从而求解出迭代关系式：
$$\begin{array}{rl}{\delta }_t(k)& =\underset{i_1,\cdots ,i_{t-1}}{\max }\mathcal{P}(o_1,\cdots ,o_t,i_1,\cdots ,i_t=q_k\mid \lambda )\\ {\delta }_{t+1}(j)& =\underset{i_1,\cdots ,i_t}{\max }\mathcal{P}(o_1,\cdots ,o_{t+1},i_1,\cdots ,i_{t+1}=q_j\mid \lambda )\\ {\delta }_{t=1}(j)& ={\delta }_t(k)\cdot a_{kj}\cdot b_j(o_{t+1})\end{array}$$
由于隐马尔可夫模型的隐状态是离散型随机变量，因此：

• $q_k,q_j\in \mathcal{Q}$，$\mathcal{Q}$表示隐状态可选择的离散值集合；
• $a_{kj}$表示状态转移矩阵$\mathcal{A}$中$i_t=q_k$行，$i_{t+1}=q_j$列对应的转移概率结果；
• $b_j(o_{t+1})$表示发射矩阵$\mathcal{B}$中$i_{t+1}=q_j$行，$o_{t+1}$列对应的发射概率结果。
  这里为简化计算，将观测变量也设置为‘离散型随机变量’。

隐马尔可夫模型的第一个缺陷在于：针对维特比算法，在求解最优隐状态序列的过程中，不得不求解各时刻隐状态取值对应的联合概率分布，并从中挑选出各时刻最优的联合概率分布。而联合概率分布求解过程并不容易，因此提高了计算代价。

隐马尔可夫模型的另一个缺陷在于：观测独立性假设。该假设定义某时刻的观测变量只与该时刻的隐变量相关，与其他变量无关：
$$\mathcal{P}(o_t\mid o_1,\cdot o_{t-1},i_1,\cdots ,i_t)=\mathcal{P}(o_t\mid i_t)$$
但在真实环境中，某一个观测变量结果，可能并非由一个隐变量决定的，而是由多个时刻的隐状态共同决定的。因而，隐马尔可夫模型的假设过强，缺乏灵活性。

最大熵马尔可夫模型介绍

最大熵马尔可夫模型(Maximum Entropy Markov Model,MEMM)本身是概率判别模型：对隐状态$\mathcal{I}$和观测变量$\mathcal{O}$的条件概率进行建模。
相比于隐马尔可夫模型，它最大的特点是抛弃了观测独立性假设，并且考虑到各时刻观测变量之间的关联关系：
$$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\prod _{t=1}^T\mathcal{P}(i_t\mid i_{t-1},o_{1:T})$$

对于每一个条件概率结果$\mathcal{P}(i_t\mid i_{t-1},o_{1:T})(t=1,\cdots ,T)$通过最大熵模型(Maximum Entropy Model)进行建模。在最大熵原理与指数族分布关系中介绍过：概率分布存在约束条件的情况下，满足约束条件下熵最大的分布就是指数族分布：
$\mathcal{Z}$又称‘配分函数’,可以看成‘归一化因子’;$h(x)$是关于$x$的函数，通常以常数形式出现。
$$\begin{array}{rl}\mathcal{P}(x)& =h(x)\cdot e^{{\lambda }^{T}f(x)-\mathcal{A}(\lambda )}\\ & =\frac{h(x)}{\mathcal{Z}}{e}^{{\lambda }^{T}f(x)}(\mathcal{Z}=e^{\mathcal{A}(\lambda )})\end{array}$$
因此，针对每一时刻的后验结果：$\mathcal{P}(i_t\mid i_{t-1},o_{1:T})$ 具体公式表示如下：
该公式不仅是‘最大熵模型’中的概率分布公式，同时也是‘指数族分布’中的概率分布公式。
$$\begin{array}{rl}\mathcal{P}(i_t\mid i_{t-1},o_{1:T})& =\frac{1}{\mathcal{Z}(o_{1:T},i_{t-1})}{e}^{{\lambda }_a^T{f}_a(o_{1:T},i_t,i_{t-1})}\\ & =\frac{1}{\mathcal{Z}(o_{1:T},i_{t-1})}\exp \left[\sum _a{\lambda }_a{f}_a(o_{1:T},i_t,i_{t-1})\right]\end{array}$$

其中，$\mathcal{Z}(o_{1:T},i_{t-1})$是关于观测变量$o_{1:T}$与过去时刻隐状态$i_{t-1}$的归一化函数；$a$表示特征集合，该集合中包含若干个特征对(pairs)$\text{<}b,i_t\text{>}$。$b$被称为 观测特征(Feature of Observation)；而$i_t$自然是目标状态(D)。$f_a(o_t,i_t)$表示特征函数(Feature Function)——对观测变量$o_{1:T}$与目标状态$i_t$的某一事实进行描述。

示例：已知特征对表示如下：
$$\text{<Is-capitalized,Company>}$$
通过该特征对发现：不仅给出了目标状态(Company)，并给出了规则：要求上一时刻隐状态给出的词汇是大写的(首字母大写)。
基于该规则，构建特征函数(Feature Function)：
$$f_{\text{<b,i>}}(o_t,i_t)=\{\begin{array}{l}1b(o_t)=True;i=i_t\\ 0otherwise\end{array}$$
假设给$o_t$一个单词：$\text{Microsoft}$(微软)，$i_t$依然给$\text{Company}$(公司)。此时：
$\text{Microsoft}$是首字母大写的单词，并且$i_t=i=Company$，针对特征函数的条件，特征函数$f_{\text{<b,i>}}(o_t,i_t)$返回结果1.
$$f_{\text{<Is-capitalized,Company>}}(\text{Apple,Company})=1$$
对应的最大熵结果自然高于$f=0$的结果。
该示例是‘寻找表示公司名字单词’的一个示例，它制定的规则很简单，只要满足首字母大写，并且该词后面是“公司”，该词就满足“是公司名字的条件”。传送门

最终，通过最大熵模型表示$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$表示如下：
从该表示可以看出，它保留了‘齐次马尔可夫假设’。
$$\begin{array}{rl}\mathcal{P}(\mathcal{I}\mid \mathcal{O})& =\prod _{t=1}^T\mathcal{P}(i_t\mid i_{t-1},o_{1:T})\\ & =\prod _{t=1}^T\frac{exp({\sum }_a{\lambda }_a{f}_a(i_t,i_{t-1},o_{1:T}))}{\mathcal{Z}(i_{t-1},o_{1:T})}\end{array}$$

基于公式的表示过程，MEMM的概率图模型表示如下：

这是从狭义角度对MEMM模型进行描述。从图中观察，它删除了观测独立性假设，使得各时刻的观测变量之间存在关联关系。
观察任意一个$\mathcal{V}$型结构，仍然以一阶齐次马尔可夫模型为例，$t$时刻的隐状态$i_t$(未知状态下)与相互独立的变量$o_t$和$i_{t-1}$相关联：
$$\mathcal{P}(i_t\mid i_{t-1},o_t)i_{t-1}\perp o_t$$
但实际上，这种狭义的模型假设对于观测变量$o_{1:T}$仍然过强，如序列标注过程中，某一时刻词语的标注结果不仅和过去的前一个词相关联，而是可能与前若干个词语甚至是整个句子序列都有关联。这种假设相比上述狭义假设更加合理。因此，广义角度的MEMM模型表示如下：

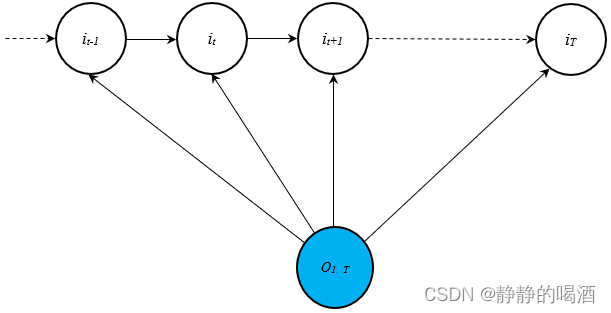
这种概率图表示彻底打破了观测变量相互独立的条件，更符合最大熵模型对于$\mathcal{P}(i_t\mid i_{t-1},o_{1:T})$的描述。

下一节将介绍隐马尔可夫模型(HMM)到最大熵马尔可夫模型(MEMM)的转化过程。

相关参考：
【中文分词】最大熵马尔可夫模型MEMM
机器学习-条件随机场（1）-背景介绍