机器学习笔记（二）回归

鲤喙

已于 2024-05-06 20:17:08 修改

阅读量3.6k

点赞数 45

分类专栏：数据分析— 机器学习文章标签：机器学习笔记回归

于 2024-04-24 14:51:19 首次发布

本文链接：https://blog.csdn.net/qq_47343046/article/details/138152442

版权

三、岭回归 (Ridge Regression)

四、LASSO 回归 (LASSO Regression)

一、线性回归

线性回归是一种用于预测的统计方法，特别适用于连续值预测。📈线性回归通过最小化误差的平方和来寻找一个线性关系，用于预测一个变量（因变量）基于一个或多个其他变量（自变量）的值。

1.1 线性回归模型

简单线性回归：仅涉及两个变量，一个是自变量，一个是因变量，公式为：

其中 y 是因变量，x 是自变量，m 是斜率，b 是截距。
多元线性回归：涉及多个自变量，形式为：

1.2 损失函数

损失函数是机器学习中用来衡量模型预测值与真实值之间差异的一个函数。损失函数的值越小，表示模型的预测值与真实值越接近，模型的性能越好。在回归问题中，常用的损失函数是均方误差（MSE）。

均方误差 (MSE)

残差（Residuals）

线性回归中，预测值（predicted）与观测值的差值称为残差，残差的本质是模型的随机误差（Random Error），是必然存在且不可学习的参数。

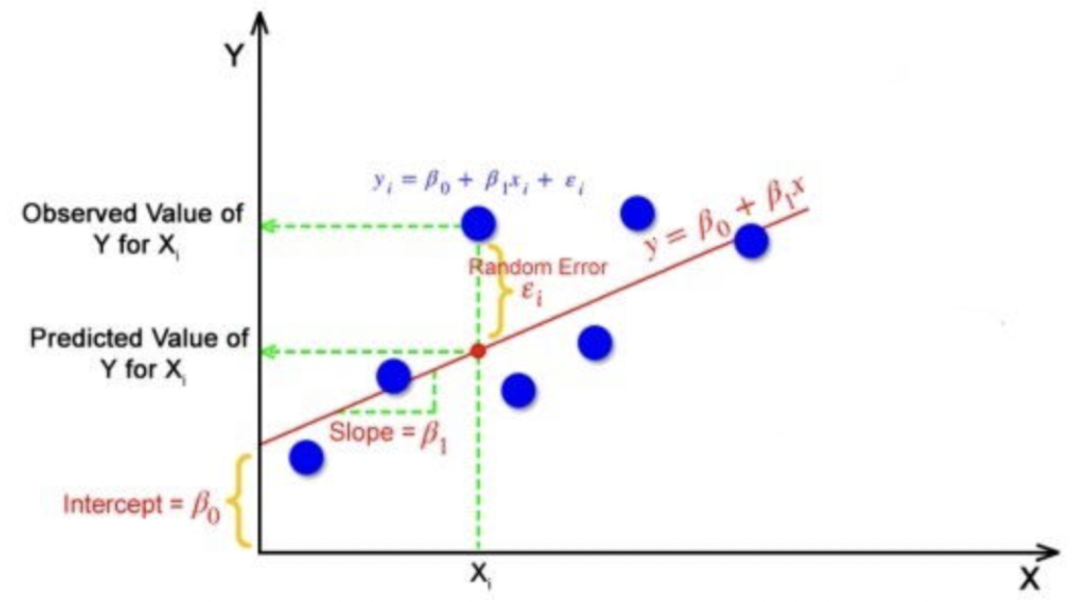
上图蓝色点表示观测值，红色点表示预测值。

最优拟合线

最优拟合线指的是线性回归模型中的一条直线，它是通过拟合训练数据得出的，使得这条直线与训练数据的残差（观测值与模型预测值之间的差异）之和最小化。

损失函数的优化（梯度下降法）

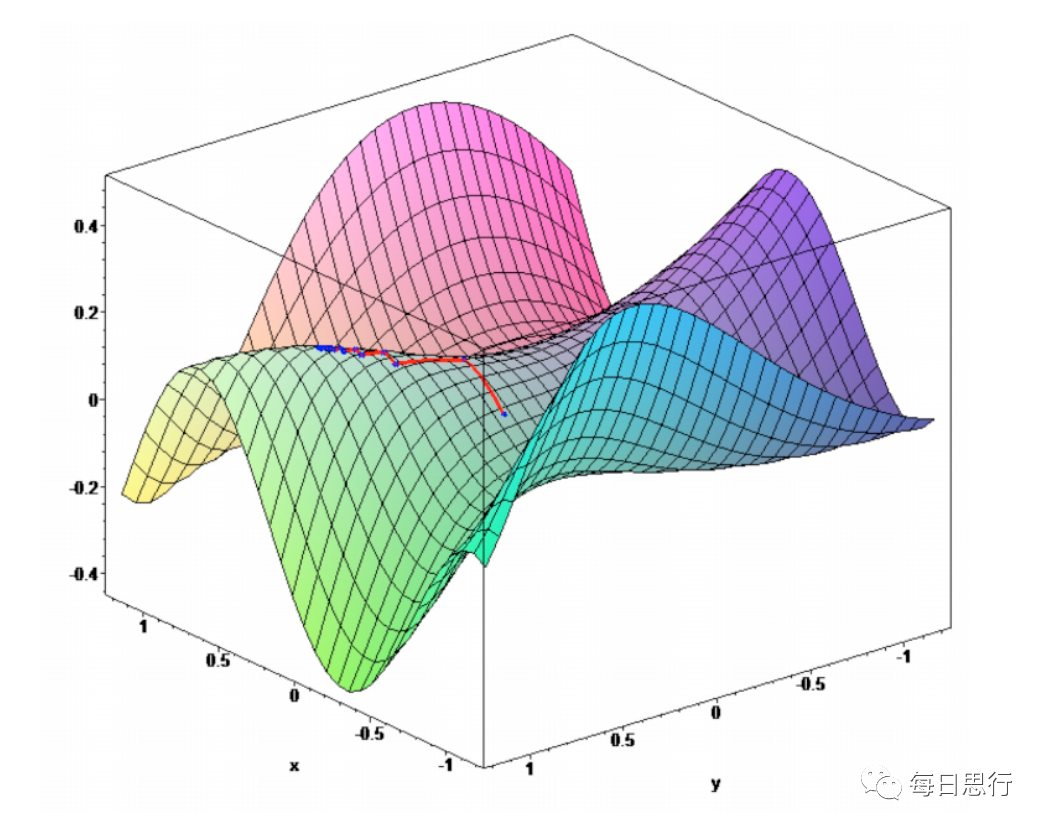
梯度下降法：是一种用于优化函数的迭代算法。它的基本思想是使用负梯度方向来逐步更新参数，使得目标函数的值逐渐减小，直到达到局部最小值或全局最小值。梯度下降算法会迭代地更新模型的参数，使得损失函数逐渐减小，直到达到收敛条件。
算法思想：先找到下降最快的方向，走到新位置再调整方向，不断重复，直到走到最低点。
若学习率太大，损失函数有可能快速达到最优值，也有可能迭代很多次也达不到最优值，

若学习率太小，则需要更多的迭代次数达到最优值。

1.3 线性回归的评价标准

我们可以使用多种评价指标度量当前的模型性能，最常用的指标包括：

R方(R2) 也称作决定系数
均方根误差(RSME)或残差标准误差(RSE)

决定系数或R方

R方指标，也称为R-Square，用于评估回归模型拟合程度。值范围在0～1之间，数值越大表示拟合效果越好，即能够更好地解释因变量的变异性。

数学表达式：

其中RSS表示残差平方和(Residual sum of Square)，TSS表示总偏差平方和(Total Sum of Squares)，总偏差平方和简称总平方和。

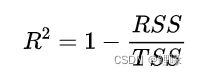
其中RSS表示残差平方和，TSS表示总偏差平方和，总偏差平方和简称总平方和。

残差平方和(RSS)的含义是衡量实际观测值和模型预测值的差异
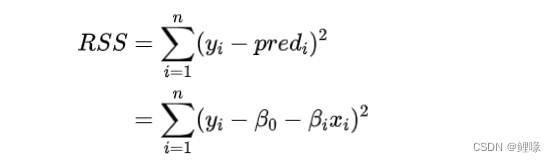
总平方和(TSS)的含义是衡量样本的分散程度。

均方根误差(RSME)

均方根误差是残差方差的平方根，表示模型对数据的绝对拟合程度，即观测值与预测值的接近程度。模型的预测误差的大小，数值越小表示模型的预测能力越好。

残差标准误差(RSE)

为了使这个估计量无偏，我们需将残差平方和除以自由度(n-2)，而不是模型中数据点的总数。这个术语被称为残差标准误差(RSE)

自由度

在线性回归中，自由度通常用于衡量模型中参数的数量。

具体来说，在简单线性回归中，有两个参数需要估计：斜率和截距。因此，自由度为样本数量减去参数的数量，即n−2。

在多元线性回归中，参数的数量取决于模型中的自变量数量。如果有 𝑝p 个自变量，则自由度为 n−p−1，其中 n 是样本数量

R方比RSME更好。因为均方根误差的值取决于变量的单位（即它不是一个归一化的度量），它可以随着变量单位的改变而改变。

1.4 假设检验

验证假设

线性回归是一种参数化方法，这意味着它对数据进行分析时做出了一些假设。为了成功进行回归分析，验证以下假设是至关重要的：

线性：需要假设因变量和自变量之间存在线性关系。如果线性关系不能清晰呈现，可以对变量X或Y进行数据转换（对数转换、多项式转换、指数转换等）以解决问题。
误差不相关性：残差项之间是相互独立的，即残差项是随机分布的，与观测变量无相关关系。如下图第一张图片的残差项是相互独立的，后一张图片不满足假设
残差是正态分布：残差是符合均值为0或接近0的正态分布，我们基于这种先验，可以判断当前的拟合直线是否为最优直线，判断方法是累加所有数据点的残差项是否为0或接近0。如果残差项不是正态分布，表明数据存在一些异常数据点，必须仔细检查数据点以训练更好的模型。
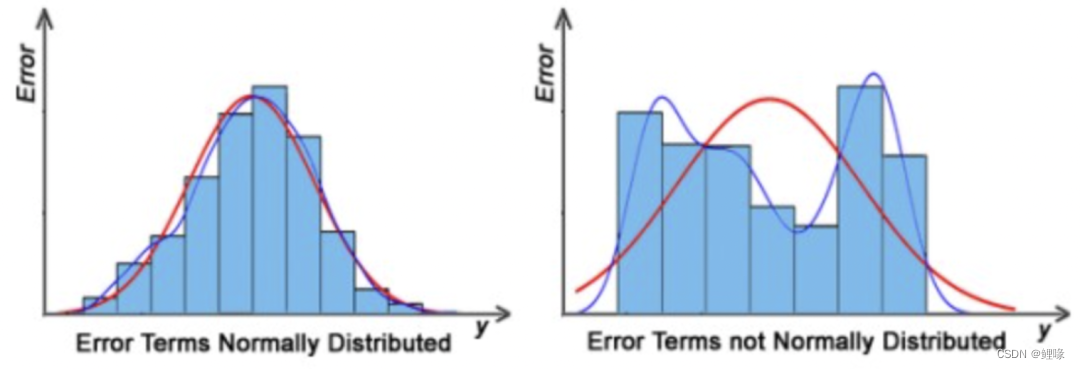
同方差性：误差是正态分布的，并具有相同的方差。这意味着对于不同的输入值࿰

最低0.47元/天解锁文章