三维坐标旋转矩阵推导过程（包看懂）

推导前提：

1. 坐标使用右手坐标系，角度逆时针旋转为正。
2. 绕X轴旋转角度为 俯仰角 即Pitch
3. 绕Y轴旋转角度为 偏航角 即Yaw（Head）
4. 绕Z轴旋转角度为 翻滚角 即Roll

一、平面二维坐标点的旋转

如右图所示,根据三角函数关系，可以列出向量OP与OP'的坐标表示形式：

x = |OP|•cosα               x′ = |OP|•cos(α+β)

y = |OP|•sinα               y′ = |OP|•sin(α+β)

将P′（x′，y′）表达式展开：

x′ = |OP|•cos(α+β) = |OP|•(cosα•cosβ - sinα•sinβ) = x•cosβ - y•sinβ

y′ = |OP|•sin(α+β) = |OP|•(sinα•cosβ + cosα•sinβ) = x•sinβ + y•cosβ

为方便运算理解，我们将二维点旋转表示为矩阵：

                                          

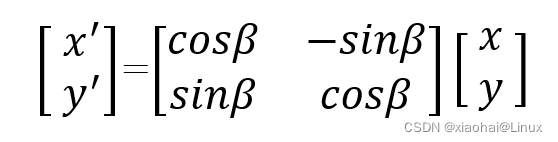
以上便是二维坐标点的旋转矩阵，接下来我们来推导三维坐标点的旋转矩阵

二、立体三维坐标点的旋转

1、绕Z轴旋转

参考二维点旋转矩阵同样的推导流程，我们可以推导出来三维点绕Z轴旋转的坐标表达式：

x′ = |OP|•cos(α+β) = |OP|•(cosα•cosβ - sinα•sinβ) = x•cosβ - y•sinβ

y′ = |OP|•sin(α+β) = |OP|•(sinα•cosβ + cosα•sinβ) = x•sinβ + y•cosβ

z′ = z

为方便运算理解，我们将三维点旋转表示为矩阵：        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        ​​​​​​​        ​​​​​​​        ​​​​​​ 

2、绕Y轴旋转

                         ​​​​​​​        ​​​​​​​        ​​​​​​​        

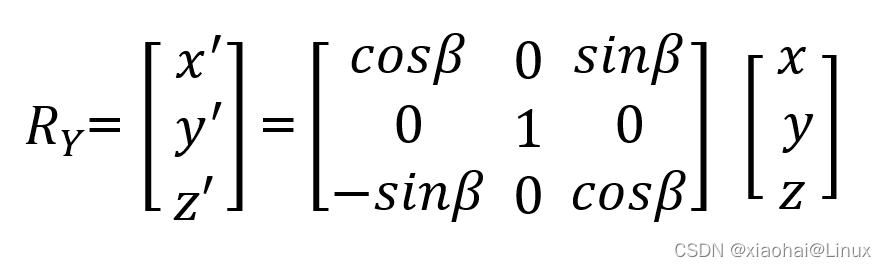
3、绕X轴旋转

        ​​​​​​​        ​​​​​​​        ​​​​​​​ 

 4、绕三轴旋转（先绕x，再绕y，最后绕z轴旋转。）

三轴全旋转矩阵 :

 整理计算后表达式为：

注：绕轴旋转的顺序不一样，得到的旋转矩阵也不一样！

综上所推导，得到三维旋转点的对应关系：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

旋转矩阵推导过程PDF文档下载