机器学习之正则化（机器学习基石）

正则化的目标

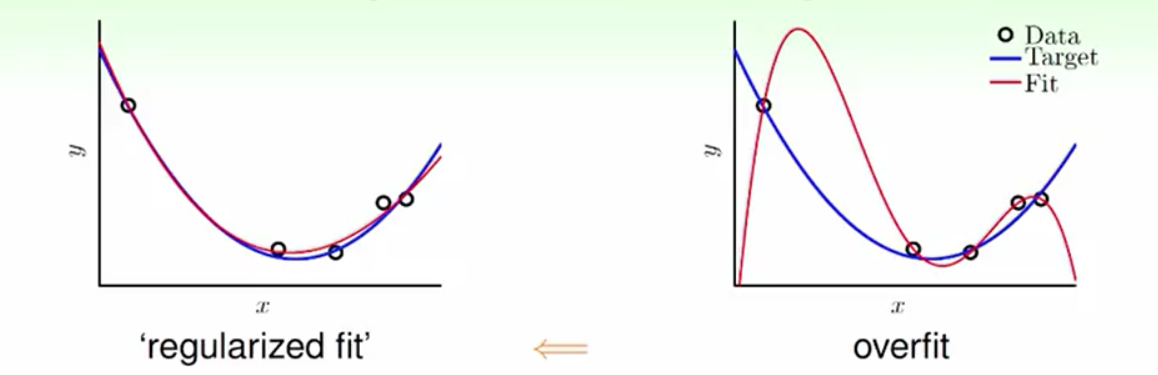
在机器学习问题中有时会由于资料量太少、有杂讯或者是学习模型的复杂度太高会导致一种Ein≈0（样本内的错误率）但是Eout（实际估计中的错误率）很高的现象这种现象就叫过拟合（详情请点击打开链接了解过拟合）。正则化的目标就是要优化这种过拟合的现象，而且正则化是通过降低模型复杂度来解决过拟合的。直观的理解如下图：

正则化的前置步骤

前提说明：在以下的案例中所有的模型都经过了特征转换，都转换成了高维空间的线性模型（特征转换请点击打开链接了解）。所以权重W都是转化过后的表示形式（高维空间的W）。最后，我们做的模型是线性回归。

明确具体手段--降维

在前面的学习中我们知道了高维度的学习模型容易过拟合，而低维度的模型不容易过拟合。所以我们想给高维度的模型进行降维就会得到一个不容易过拟合的模型。而且高维度的模型与低维度的模型有如下的关系：

高维度模型是低维度普适情况，低维度是高维度的特殊情况。以10维与2维的模型举例，当10维的后8维权重W等于0的时候它也就变成了2维的模型。

更为宽松一点的条件就是任意的8个维度的权重W等于0这样我们得到的模型也与一个2次模型有类似的简单，它的复杂度介于2维与10维之间与此同时要解决这个模型是一个NP-hard问题。

降维的转换

我们相信在10维的模型中且大部分维度为0的时候的权重（W）之和是一个很小的数。那么我们就将这个任意8个W等于0的条件改为所有W²之和的小于某一个常数C，这样会使我们得到相似的结果但是计算会变得比较简单。与此同时较大C的模型也会包含较小C的模型。

进行正则化（基于降低权重平方之和）

问题向量化

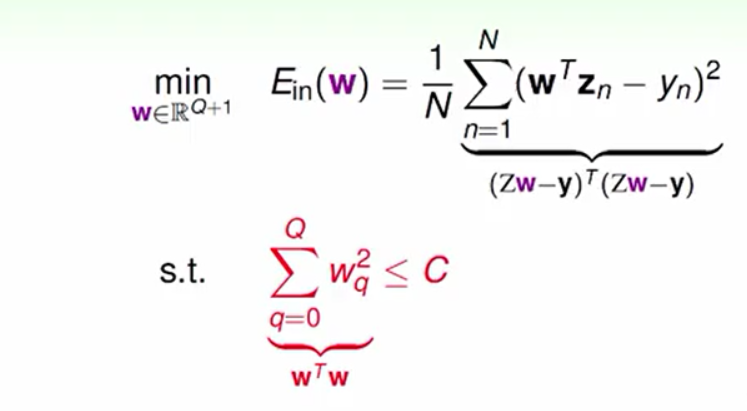
将上述问题明确的写出来同时为了运算的方便我们将问题进行向量化如下图：

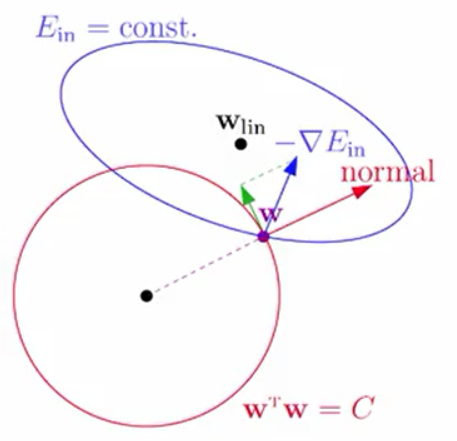
我们的目的就是在W²之和小于C的情况下最小化Ein。其中，W²之和小于C可以理解为一个向量的长度小于一个常数，它的几何意义就是半径的平方为C的球。将这个问题用几何的方式表达出来如下图：

在图中，球空间代表我们的正则化约束，椭圆空间代表梯度，Wlin代表梯度为0的点。我们的目标就是要求在球的范围内找到距离Wlin最近的点。W会指向的球的一点，球在该点的法向量为normal。W运动的条件是梯度的反方向在垂直于normal的方向上有分量。我们的终点是W（之所以这样说是因为normal与W的方向一致）与梯度的方向平行（这时的W我们特殊称之为WREG），这个时候我们没有办法继续靠近Wlin，这样就完成了我们的带条件的优化。

因为我们的W与梯度的方向平行，再加上我们把它们的比值假设为2λ/n则有下面的等式：

这就是拉格朗日乘子法，专门解决带条件的优化问题。

问题的转换

λ是两个向量的比值所以它大于0，如果现在有人告诉我λ的确切的值我们的问题将会与线性回归的最优化十分相似。具体推导过程如下：

这个优化求解过程就叫Ridge Regression（山脊回归），用来求带有条件的线性回归问题。

问题的进一步转换

事实上要是有个人在刚开始告诉我λ我们我问题可以变形如下：

我们之所以求解梯度是因为我们要求Ein(W)的最小化问题，所以我们将上式求积分还原到最初我们想求的问题。这样一个带有约束的问题变成了一个没有约束条件但是多带一项的最优化问题，我们现在想要最小化的就是图中的Eaug(W)。

对于使用者来说告诉我们常数C与告诉我们λ有类似的难度，所以当我们通常选择直接拿到λ，这时候我们就可以不做转换直接去解一个多带一项的最优化问题。

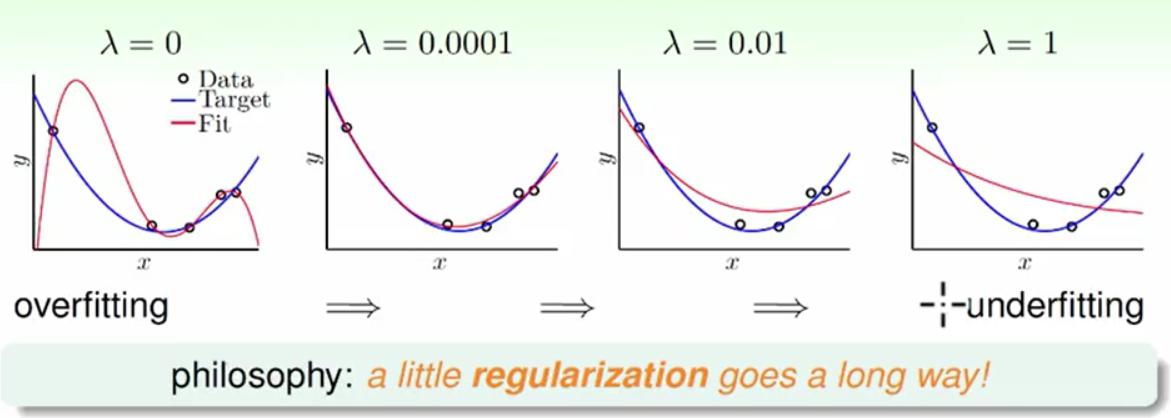
λ的选择

从上图的经验中分析来看，我们只要一个很小的λ就能使得正则化得到很好的效果。这里的λ就相当于对高维度的W的惩罚，从这点来看λ与C的功能相似。正是因为对高维度的W的惩罚所以这样的正则化就叫weight-decay Regularrization。在案例中我们做的事情是线性回归而这种正则化也可以推广到罗吉斯回归，和二元分类的转换中。

一个小细节

假设在特征转换之后得到一个高次的多项式，如果这时的x∈[-1,+1]那么x的高次方将会变得很小，如果这一项想要在多项式中体现出影响力来那么我们就得要求W很大这与我们的正则化的目标相反，这时我们的正则化就过度的惩罚了这些高次的W。为了使这个问题得到平衡，我们在这里提出的建议是在解决一个多项式的正则化的时候直接使用Legendre多项式就能得到不错的结果。

正则化与VC维度的关系

做正则化间接做好了Ein

在以前求Eout的过程中Eout<=Ein(W)+Ω(H(C))，这里的模型复杂度是一个带有约束的假设集合模型复杂度为Ω(H(C))。现在的求解中Eaug与以前的Eout有类似的性质，Eaug的复杂度为单个假设的复杂度Ω(W)。VC给我们的保证是Ω(H(C))与Ω(W)有很大的相似程度，所以我们在做好Eaug的同时也做好了Eout（Eaug是Eout的代理人）而且想对于以前的只做好Ein的效果更好。

正则化使得VC维度更加有效

在正则化的过程中我们加入了约束条件使得模型复杂度变成了有约束的Ω(H(C))。实务上我们在考虑假设模型的时候我们考虑了所有的模型但是也考虑了最后算法的的选择，这样就使得我们的普通的VC维度变成了现在的有效VC维度，大大降低了模型复杂度。

正则化的推广

正则化方式的类型

正则化就是在训练学习模型的时候给学习算法加一些限制条件以防模型会过拟合，一般我们会有以下的三种加条件的方式：

1.把我们知道的一些目标函数的特质或大致方向加进去。

2.尽量去选择一些简单的平滑的，比较严格的（能够说服我们的）学习模型（比如说L1的正则化，等等介绍）。

3.选择一些友好的容易去优化的规则（比如上文中介绍的weight-decay的正则化方法）。

在以前的错误衡量上我们也有三种方式可选，在实务上我们在综合考虑错误衡量的时候会考虑错误衡量的限制与正则化的限制的综合影响。

L1的Regularizer

在上文中提到的weight-decay（L2）的正则化中我们的限制条件是||W||²之和小于一个常数C。现在介绍的L1的正则化限制是||W||之和小于一个常数C。它的几何意义是高维空间的菱形球体。它有如下性质：

1.w为0时是这个函数的尖点所以在菱形球体的顶点处不可微分。

2.在菱形的边上菱形平面的法向量常常与梯度的方向不平行。

结论：我们常常在菱形的尖点处得到最优解，此时W的大多数维度都等于0我们得到了一个稀疏的结果。就像是一个300维的向量在经过L1的正则化之后只有20个不为0的维度我们只需要计算着20个维度就能够较好的解决问题，这样也达到了降维的效果。