机器学习之核函数逻辑回归（机器学习技法）

从软间隔SVM到正则化

从参数ξ谈起

在软间隔支持向量机中参数ξ代表某一个资料点相对于边界犯错的程度，如下图：

在资料点没有违反边界时ξ的值为0，在违反边界时的值就会大于0。所以总的来说ξ的值等于max(1 - y(WZ + b) , 0)。所以我们把问题合并如下：

这样这个问题就变成了一个没有条件的问题。

与L2正则化的关系

上述简化后的问题与L2的正则化极其相似：

它们的目标都是最小化W²与一个错误衡量的和。在软间隔的SVM中用来做正则化的是W，我们希望有小的W这样就会有LargeMargin。在L2中我们也是希望W有较小的维度这样就不至于模型复杂度过高。

为什么不以正则化的角度出发去推导软间隔SVM？

①在这个简化问题上，没有一次的约束条件所以我们很难想象去用二次规划工具去解决。当然也就不会用到关于对偶与核函数的方法。

②在这个简化问题上，max()函数在某些点上不可微分很难最小化。

总的来说如果以正则化的角度出发去推导软间隔SVM会使得问题非常难解。

关联的目的

写到这里我们知道了SVM就像是一个正则化的模型我们总结如下：

无论是SVM的LargeMargin还是L2的限制（事实上是维度上的限制）都会得到更少的超平面减少了模型过拟合的危险。软间隔是我们估算错误的一种方式。

我们之所以将SVM看成是一个正则化的模型是因为我们希望SVM以一种新的角度去做更多的事情（比如说回归问题，etc.）。

软间隔SVM的错误衡量

与二元分类的错误衡量的关系

软间隔SVM在衡量一个资料的犯错误情况时就是在看这个资料点的违反边界的情况也就是ξ的值，它等于max(1 - y(WZ + b) , 0)。以ys（s为得分函数）的值作为横轴，犯错误的情况为纵轴。分别画出SVM错误与0|1错误的错误衡量如下图：

图中的折叶式曲线为SVM的错误衡量曲线，我们能够明显看出SVM的错误衡量曲线是0/1错误函数的上限（准确的来说是凸的上限）。

与LogisticRegression错误衡量的联系

将LogisticRegression的错误函数作一个放缩的动作放到上图的坐标系中得到：

图中橘色的曲线就是LogisticRegression的错误衡量曲线。从直观上感觉它与SVM的错误衡量曲线很相似。它们都有以下特征：

从+∞与-∞两个极端的情况来看LogisticRegression的错误与SVM的错误几乎一样，从这种角度来开SVM就像是在做L2正则化的LogisticRegression。（一个是最大的边距，一个是W的降维处理）

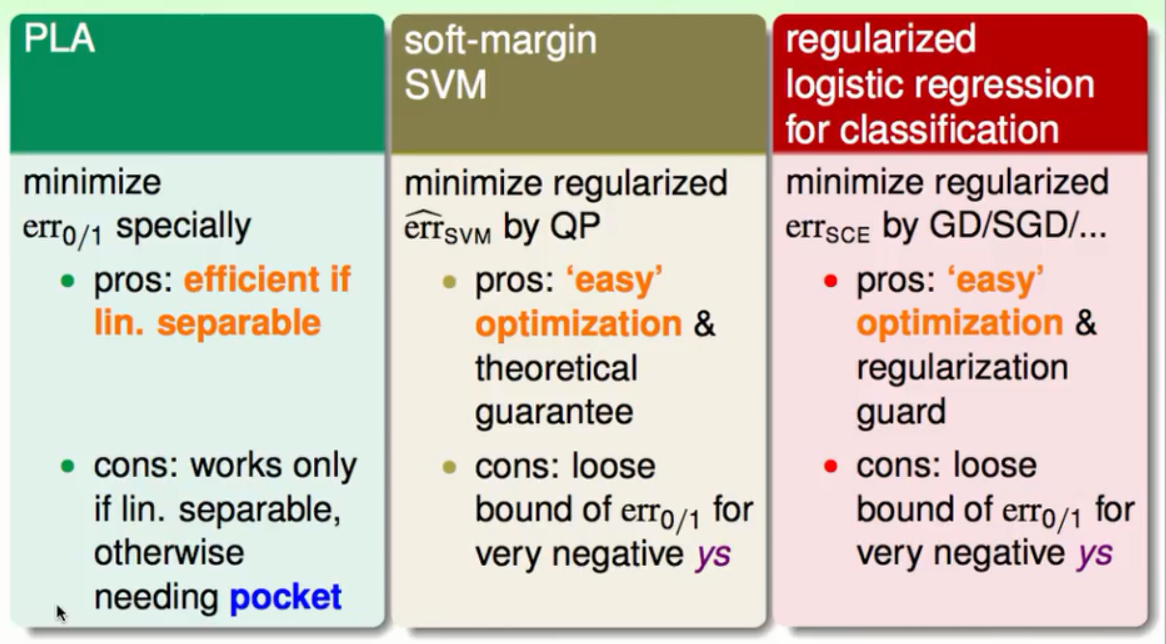
用线性模型做二元分类

①PLA算法直接去衡量在一笔资料上是否犯错进而去优化模型，但是它要求资料是线性可分的。即使是pocket也是一个NP-Hard问题。

②SVM是通过二次规划区优化模型的，比叫简单而且也有理论上的保障。但是在做二元分类的问题上它只得到一个上限。

③L2正则化的LogisticRegression通过梯度下降法（或者是随机梯度下降法）来优化模型，比叫简单也有正则化的保证。但是在做二元分类的问题上它只得到一个上限。

小节：我们解决了一个L2正则化的LogisticRegression就几乎解决了一个SVM的问题。

SVM做软间隔二元分类

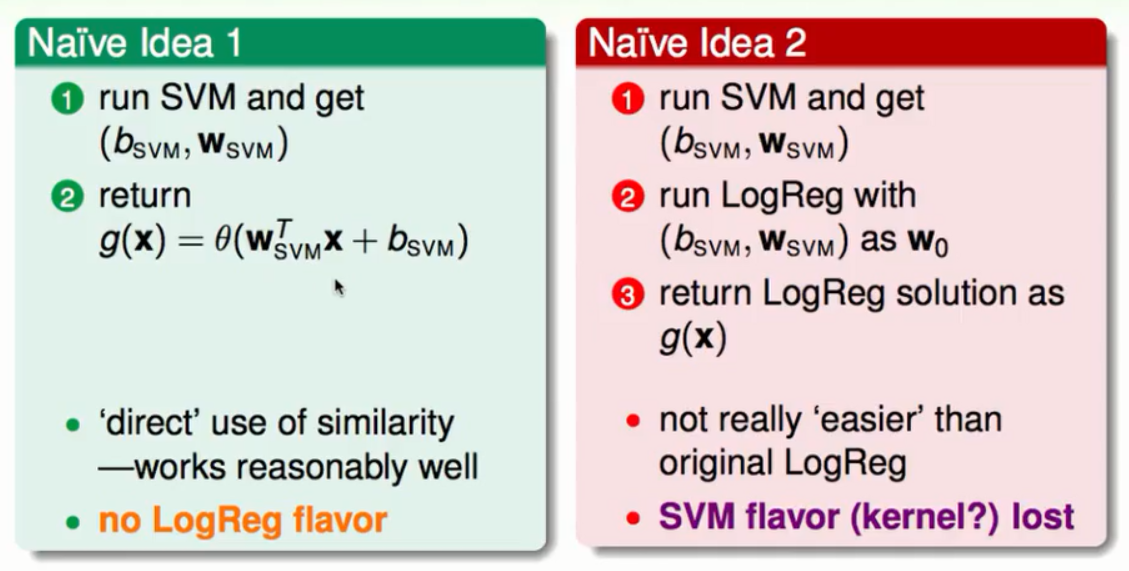
简单的组合

既然SVM与LogisticRegression有很大的相似性，我们试着将SVM与LogisticRegression结合起来去做软性的二元分类。

方法一：得到SVM的结果然后映射到S型函数上，这种方法表现的还不错但是没有体现出LogisticRegression最优化时极大似然估计的特征。

方法二：得到SVM的结果，以这个结果为起点去做LogisticRegression，但是这样的做法与直接去做一个LogisticRegression没有什么区别。因为后面的效果将前面的SVM的功劳覆盖了。

二者兼顾的组合

①我们先用SVM得到W与b的值。

②将这个值进行一些放缩，并映射到S型函数上。如下图所示：

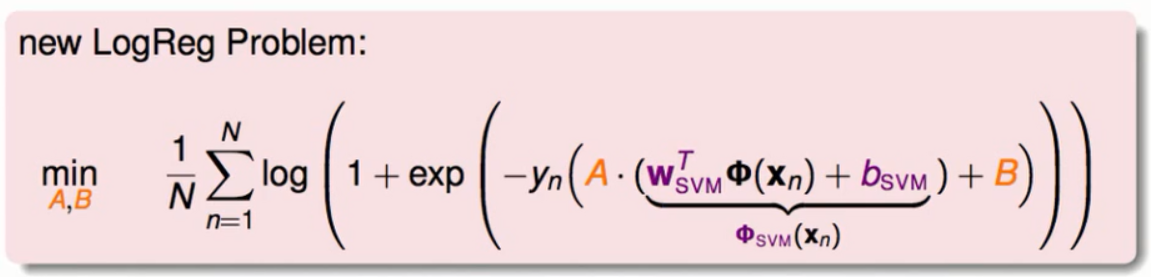
整体来看先用SVM做出了大体上的结果又用LogisticRegression进行了微调。从形势上看，整个式子与LogisticRegression最优化时的结构很相似（如下图），其中B的值是做一些十分微小的微调。在这里更把SVM的前置操作当做是对资料X的一种特殊转换。

理论上来说：

①A的值应该大于0，如果小于0的话证明在一开始的时候我们的SVM在乱做。

②B的值约等于0，在SVM做好之后不应该有太大的调整。

将上述的式子更加具体化得到下图：

当SVM计算完毕的时候我们将X这个多维的转换为一个一维的数字我们对这个数字做放缩和平移的动作，在第二阶段我们只是在解决一个单一维度的两个变数的逻辑回归问题。

总的来说这个模型的解决如下：

这个模型的结果与只有SVM做出来的结果略有不同因为有B做微调的动作。由于只有两个变数我们除了用（随机）梯度下降法之外我们还可以使用其他的方法来得到最优解。

小节：我们用SVM的方式得到了LogisticRegression在Z空间（特征转换空间）的解。

核函数逻辑回归

核函数背后的关键

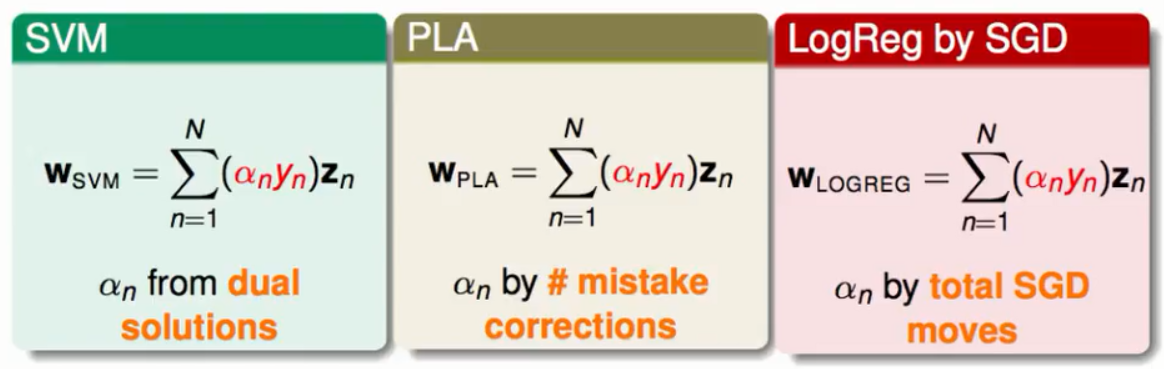
在做SVM的时候核函数是计算一堆Z的内积的方法，而在最终的模型中也能够使用核函数的原因是最优的W的解能够写成一堆Z的线性组合（称之为representer theorem）如下图：

而在我们以前学过的算法中也出现过最优的W的解能够写成一堆Z的线性组合如下：

①SVM中的系数α是从对偶问题的结果中来。

②PLA中的系数α是来自我们训练的过程里每个Z到底参与了多少错误修正的过程来得到的。

③LogisticRegression中的系数α来自于在梯度下降的时候梯度告诉我们走的情况。

我们想要将核函数的方法应用到上述这些情景中来更加方便的解决在Z空间（特征转换）的问题。

representer theorem

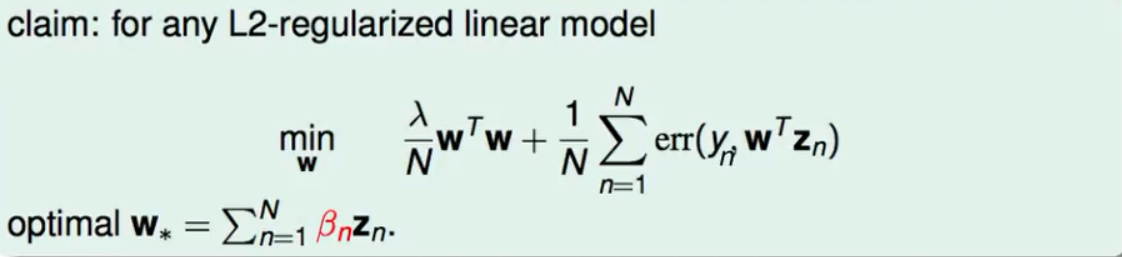
至于什么时候能够使用representer theorem 这个理论，在数学上给出了这样的结果：如果现在解决的是一个L2正则化的线性模型的问题，它的最佳化W的可以使用一堆Z的线性组合来表示，如下图：

representer theorem 的证明

①将最佳的W（这里用W*来表示）分解成与Z空间平行的部分W||，和与Z空间垂直的部分W⊥。我们有一个假设：如果W*能够用Z来完全表示的话那么W⊥的值肯定为0。

②我们使用反证法，既如果W⊥不为0则有下面的情况：

最重要的是在计算W*的内积的时候会有W*的内积>W||的内积，这样W||就成为了最优解这显然与我们的假设矛盾，所以W⊥不为0这个假设不成立。这就是representer theorem为什么可行。我们得到最强烈的信息就是凡是进行L2正则化的线性问题我们都能将核函数的技巧用到上面。

核函数逻辑回归

我们将用核函数的方法来解决一个L2正则化的逻辑回归如下图：

我们直接将W*表示成β的形式带到我们最佳化的问题中，然后就得到一个关于β的无条件的最佳化问题。这时我们可以用梯度下降法或随机梯度下降法来得到问题的最优解。

核函数逻辑回归的全新角度

再仔细观察核函数逻辑回归之后会发现它可以是一个关于β的线性模型：

其中kernel函数既充当了转换的角色有充当了正则化的角色，这种角度同样适用于SVM演算法。需要注意的是：SVM的解α大多都是0，核函数逻辑回归的解β大多都不是0这样我们会付出计算上的代价。