数字图像处理学习笔记（四）

第七章小波和多分辨率处理

引言

傅里叶变换一直是 基于变换的图像处理 的基石。

近年来一种新的称为小波交换的变换使得压缩、传输和分析图像变得更为容易。与基函数为正弦函数的傅里叶变换不同，小波变换基于一些小型波，称为小波，它具有变化的频率和有限的持续时间

小波变换被称为多分辨率理论的基础

多分辨率理论涉及多个分辨率下的信号（或图像）表示与分析。这种方法的优势很明血，某种分辨率下无法检测的特性在另一种分辨率下将很容易检测。

7.1 背景

从数学角度看，图像是一个具有局部变化的统计特性灰度值的二维阵列．而该统计特性是类似边缘和对比同质区域突变特性的不同组合导致的。

图像金字塔：

一个图像金字塔是一系列以金字塔形状排列的、分辨率逐步降低的图像集合。金字塔的底部是待处理图像的高分辨率表示，而顶部则包含一个低分辨率近似。当向金字塔的上层移动时，尺寸和分辨率降低。

基础级 J的大小为 $2^J\times 2^J或N\times N$，其中 $J=Lo{g}_{2}N$，

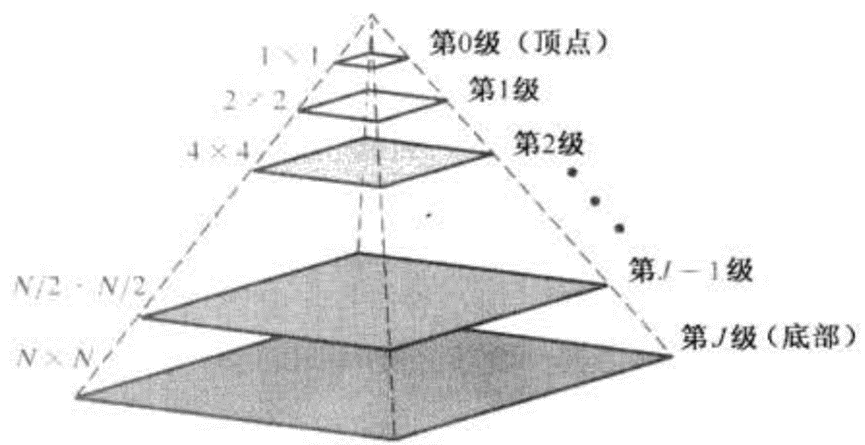
图像金字塔可以由上采样和下采样实现
上采样可看成是在序列中的每一个样本后插入；
下采样可看成是每隔一个样本丢弃一个样本。、

子带：
在子带编码中，一幅图像被分解为一组频带受限的分量． 称为子带。

有限冲激响应滤波器 (FIR）：

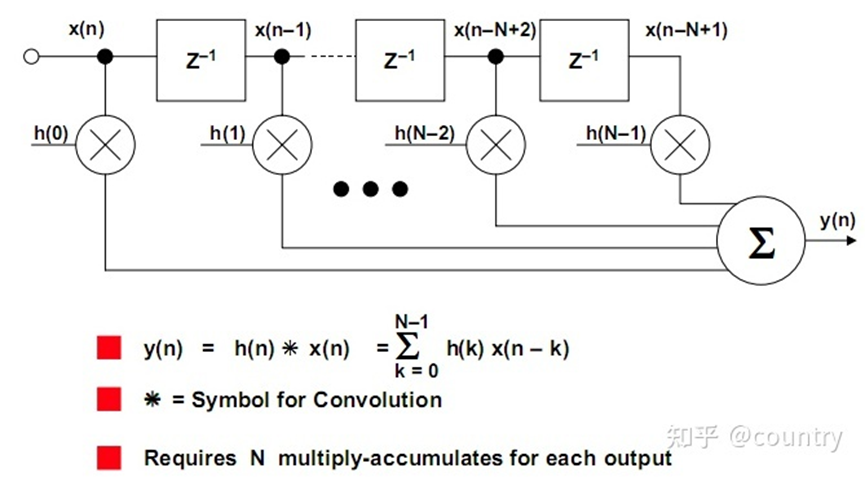
FIR滤波器是非递归型滤波器的简称，又叫有限长单位冲激响应滤波器。带有常系数的FIR滤波器是一种LTI(线性时不变)数字滤波器。冲激响应是有限的意味着在滤波器中没有发反馈。长度为N的FIR输出对应于输入时间序列x(n)的关系由一种有限卷积和的形式给出，具体形式如下：

$$y(n)=\sum _{k=0}^{N-1}h(k)x(n-k)$$

直接形式FIR滤波器图解：

哈尔变换:

哈尔变换可以用如下矩阵形式表示 ：
$$T=HF{H}^T$$
F 是一个NxN的图像矩阵，H 是一个 NxN 的哈尔变换矩阵， T 是一个 N× N 的变换结果。
哈尔基函数为

$$h_0(z)=h_{00}(z)=\frac{1}{\sqrt{N}},z\in [0,1]$$
$$h_k(z)=h_{pq}(z)=\frac{1}{\sqrt{N}}\{\begin{array}{ll}{2}^{p/2},& \text{(q−1)/2p≤z<(q−0.5)/2p}\\ -2^{p/2},& \text{(q−0.5)/2p≤z<q/2p}\\ 0,& \text{其他，z∈[0,1]}\end{array}$$

N = 2” 为了生成矩阵H，定义整数 k，即 k = 2p+q-1 ， 其中 0≤ p ≤n - 1 ，当 p=0 时， q=0 或1，而当p≠0时， 1≤q≤2p 。
2 × 2哈尔矩阵是

$$H_2=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$

4×4哈尔矩阵是

$$H_2=\frac{1}{\sqrt{4}}\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 1& -1& -1\\ \sqrt{2}& -\sqrt{2}& 0& 0\\ 0& 0& \sqrt{2}& -\sqrt{2}\end{array}\right]$$

7.2 多分辨率展开

级数展开

信号或函数f(x）通常可以被很好地分解为一系列展开函数的线性组合 ：

$$f(x)=\sum _k{\alpha }_k{\phi }_k(x)$$

k 是有限和或无限和的整数下标，${\alpha }_k$是具有实数值的展开系数，${\phi }_k(x)$是具有实数值的展开函数。

尺度函数

考虑由整数平移和实数二值尺度、 平方可积函数ψ(x）组成的展开函数集合，即集合｛${\phi }_k(x)$} •其中
$${\phi }_{j,k}(x)=2^{j/2}\phi (2^{j}x-k)$$
对所有的 $j,k\in Z$ 和$\phi (x)\in L^2(R）$都成立,这里， k 决定了${\phi }_{j,k}(x)$沿 x 轴的位置，j决定了${\phi }_{j,k}(x)$的宽度，即它沿 x 轴宽或窄。 项 2j/2控制函数的幅度。 由于φi.k (x） 的形状随j 发生变化，所以 $\phi (x)$称为尺度函数。

简单尺度函数遵循多分辨率分析的 4 个基本要求：

1. 尺度函数对其整数平移是正交的。
2. 低尺度的尺度函数跨越的子空间嵌套在高尺度跨越的子空间内 。
3. 唯一的对所有$V_j$通用的函数是f(x) =0。
4. 任何函数都可以以任意精度表示。

改进等式、 MRA 等式或扩张等式:
$$\phi (x)=\sum h_{\phi }\sqrt{2}\phi (2x-n)$$
该递归等式中的系数 $h_{\phi }(n）$称为尺度函数系数；$h_{\phi }$为尺度向量。
它表明任意子空间的展开函数都可以向其本身的双倍分辨率副本来建立，即来自相邻较高分辨率空间的展开函数。

因为小波空间存在于自相邻较高分辨率尺度函数跨越的空间中，所以任何小波函数可以表示成平移后的双倍分辨率尺度函数的加权和。

$$\psi (x)=\sum _n{h}_{\phi }(n)\sqrt{2}\phi (2x-n)$$

$h_{\phi }(n)$称为小波函数系数，$h_{\phi }$ 为小波向量。

7.3一维小波变换

小波级数展开：
$$f(x)=\sum _k{c}_{j0}(k){\phi }_{j0,k}(x)+\sum _{j=j_0}^{\infty }\sum _k{d}_j(k){\psi }_{j,k}(x)$$
$c_{j0}(k)$通常称为近似和／或尺度系数，$d_j(k)$称为细节和／或小波系数。
$$c_{j0}(k)=⟨f(x),{\phi }_{j0,k}(x)⟩=\int f(x){\phi }_{j0,k}(x)dx$$
$$c_{j0}(k)=⟨f(x),{\psi }_{j,k}(x)⟩=\int f(x){\psi }_{j,k}(x)dx$$

离散小波变换

小波级数展开将一个连续变量函数映射为一系列系数，如果待展开的函数是离散的（即数字序列），得到的系数就称之为离散小波变换（DWT）

连续小波变换

离散小波变换的自然延伸是连续小波变换（CWT），连续小波变换将一个连续函数变换为两个连续变量（平移和尺度）的高冗余度函数。 变换结果在时间－频率分析时很容易解释并有很大的价值。

7.4 快速小波变换

快速小波变换（FWT）是一种实现离散小波变换（DWT）的高效计算，该变换使用了相邻尺度 DWT系数间的一种幸运的令人惊讶的关系。 它也称为 Mallat 人字形算法。

7.5二维小波变换

大小为 M x N 的图像f(x, y）的离散小波变换是

$$W_{\phi }(j_0,m,n)=\frac{1}{\sqrt{MN}}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y){\phi }_{j0,m,n}(x,y)$$
W φ i ( j , m , n ) = 1 M N ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) ψ j , m , n i ( x , y )   , i = { H , V , D } W_{ \varphi}^{i}(j,m,n) = \frac{1}{\sqrt {MN}}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)\psi_{j,m,n}^{i}(x,y) \ , i=\{H,V,D\} Wφi​(j,m,n)=MN ​1​x=0∑M−1​y=0∑N−1​f(x,y)ψj,m,ni​(x,y) ,i={H,V,D}

$j_0$是一个任意的开始尺度，$W_{\phi }(j_0,m,n)$ 系数定义f (x, y) 在尺度$j_0$处的近似。$W_{\psi }^i(j,m,n）$ 系数对尺度 $j\le j_0$附加了水平、 垂直和对角方向的细节。
小波在图像处理中的基本方法是：

• 计算一幅图像的二维小波变换。
• 修改变换。
• 计算反变换。

DWT的尺度和小波向量被用做低通和高通滤波器，所以大多数基于傅里叶的滤波技术与“小波域”部分是等价的。

7.6 小波包

快速小波变换将一个函数分解为其宽度呈对数关系的尺度函数和小波函数的和，即（函数的）低频内容使用较窄带宽的（尺度和小波）函数来表示，而高频内容使用较宽带宽的函数来表示。如果我们想要更大地控制时间-频率平面的分开度（即在较高频率处频带较小），则必须对 FWT 加以推广，以便得到一个更为灵活的分解，这种分解称为小波包。

7.7小结

本章主要介绍了图像处理中的小波和多分辨率分析的数学基础。基本上是数学概念。二维小波变换则对应的为图像处理的相关内容。小波和小波变换与傅里叶变换具有相似性。我们重点应该关注小波变换在于图像处理中能起到的作用。
（本章确实没怎么看懂，只接触了相关的概念，后面需要再看一下小波相关的资料）

第 8 章图像压缩

图像压缩是一种减少描绘一幅图像所需数据量的技术和科学，它是数字图像处理领域中最有用和商业上最成功的技术之一。

8.1 基础知识

数据压缩：

是指减少表示给定信息量所需数据量的处理。
如果我们令 b 和 b’代表相同信息的两种表示中的比特数（或信息携带单元），那么用 b 比特表示的相对数据冗余 R 是
$$R=1-1/C$$
C通常称为压缩率，定义为C=b/b’

二维灰度阵列受三种主要类型的数据冗余的影响 ：
1、编码冗余 。2、空间和时间冗余。3、不相关的信息。

编码冗余

当对事件集合（例如灰度值）分配码的时候 ． 如果不取全部事件概率的优势，就会出现编码冗余。当用自然二进码表示一幅图像的灰度时，编码冗余几乎总是存在的。 其原因是大多数图像都是由规则的、在某种程度上具有可预测形态（形状）与反差的物体组成的，并且这些图像被取样，所以，描述的物体远大于图像元素。

空间冗余和时间冗余

多数图像中，像素是空间（在 x 和 y方向）和时间相关的（当该图像是视频序列的一部分时），因为多数像素灰度可根据相邻像素灰度进行合理的预测，所以单个像索携带的信息较少。 在这种意义上，一个像素可由其相邻像素推断出来，那么它的视觉贡献的大多数就是冗余的。

不相关的信息

照缩数据集最简的方法之一是从集合中消除多余的数据。在数字图像压缩方面．被人的视觉系统忽略的信息或与图像预期的应用无关的信息都是删除的候选者。

图像信息的度量

一个具有概率 P（E）的随机事件 E可被说成是包含
$$I(E)=log\frac{1}{P(E)}==-log\frac{1}{P(E)}$$
单位的信息

当信息源的输出依赖于前面有限数量的输出时，那么该信源称为马尔可夫信源或有限记忆信源。

去除与视觉不相关信息会导致真实的或一定数量的图像信息的丢失。因为信息的丢失，因此需要一种量化这种丢失的本质的方法。两类准则可用于这样的评估：
（1）客观保真度准则；（2）主观保真度准则。

信息损失可以表示为压缩处理的输入和输出的数学函数时，则称其是以客观保真度准则为基础的。

主观评估是通过向观察者显示解压缩的图像， 并将他们的评估结果进行平均得到的 。

图像压缩模型

图像压缩系统是由两个不同的功能部分组成的 ： 一个编码器和一个解码器。 编码
器执行压缩操作．解码器执行解压缩的互补操作。

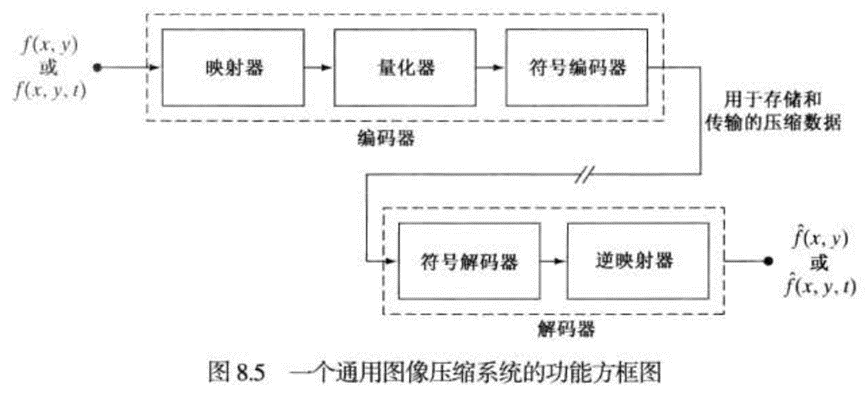
图像格式、 容器和压缩标准

在数字图像处理领域，图像文件格式是组织和存储图像数据的标准方法。它定义了所使用的数据排列的方式和压缩的类型——如果有的话。一个图像容器类似于文件，格式，但处理多种类型的图像数据。 另一方面， 图像压缩标准对压缩和解压缩图像定义了过程，也就是定义减少表示一幅图像所需数据量的过程。 这些标准是图像压缩技术被普遍接受的基础。

8.2 一些基本的压缩方法

霍夫曼编码

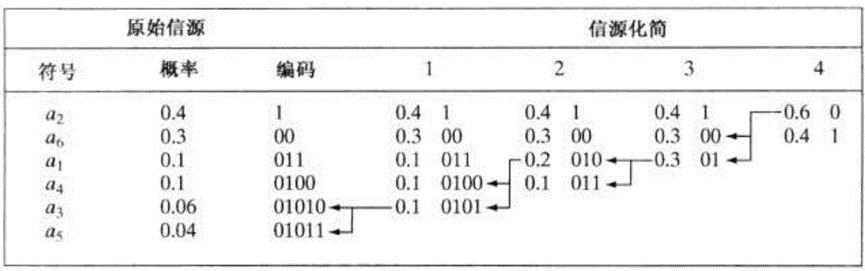
霍夫曼方法的第一步是通过对所考虑符号的概率进行排序，并将具有最小概率的符号合并为一个符号来替代下次信源化简过程中的符号，从而创建一个简化信漉系列。
霍夫曼编码过程的第二步是对每个化简后的信源进行编码，从最小的信源开始． 并直到遍历原始信源。

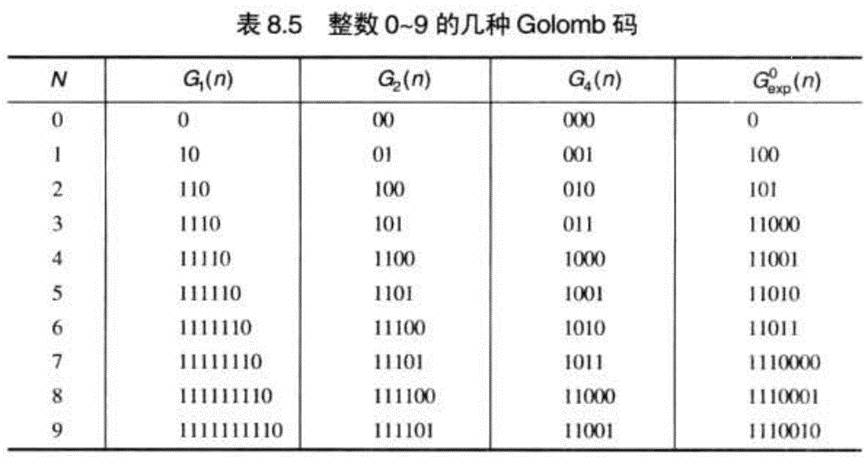
Golomb 编码

给定一个非负整数 n 和一个正整数除数 m>0后，表示为 Gm(n)的n关于m的 Golomb 编码是商[ n/m]的一元编码和 n mod m 的二进制表示的一个合并。

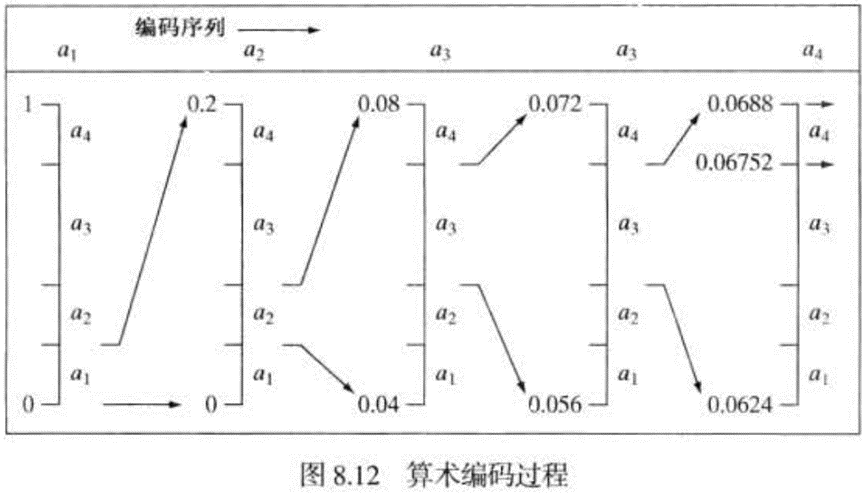
算术编码

算术编码给信源符号（或消息）的整个序列分配了一个单一的算术码字。 这个码字本身定义了一个介于0和1之间的实数间隔。当消息中的符号数量增加时，用于表示消息的间隔会变小，而表示该间隔所需的信息单位（假设为比特）的数量则会变大。消息的每个符号根据其出现的概率来减小该区间的大小。

LZW 编码

在编码过程的开始阶段，先构建一个包含被编码信源符号的码书或字典。对于8 比特单色图像，字典中的前256个字被分配给灰度值0, 1, 2， … ， 255 。当编码器顺序地分析图像像素时，不在字典中的灰度序列被放置在算法确定的位置（即下一个未用的位置） 。

行程编码

沿其行（或列）重复灰度的图像，通常可用相同灰度的行程表示为行程对来压缩，其中每个行程对指定一个新灰度的开始和具有该灰度的连续像素的数量。

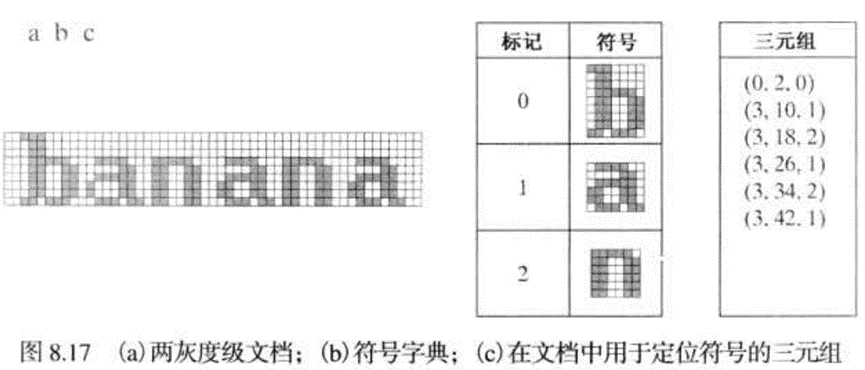
基于符号的编码

一幅图像被表示为多幅频繁发生的子图像的一个集合，称为符号。 每一个这样的符号都存储在一个符号字典中，且该图像以一个三元组｛(x1，Y1, t1),（x2，Y2, t2) 的集合来编码。其中，每个（xi,yi）对规定了图像中一个符号的位置，而记号ti是该符号或子图像在字典中的地址。也就是说每一个三元组表示图像中一个字典符号的一个实例。通过仅存储一次重复的符号，可以有效地压缩图像。

比特平面编码

把一幅多级（单色或彩色）图像分解为一系列二值图像，并使用几种熟知的二值压缩方法之一来压缩每幅二值图像。

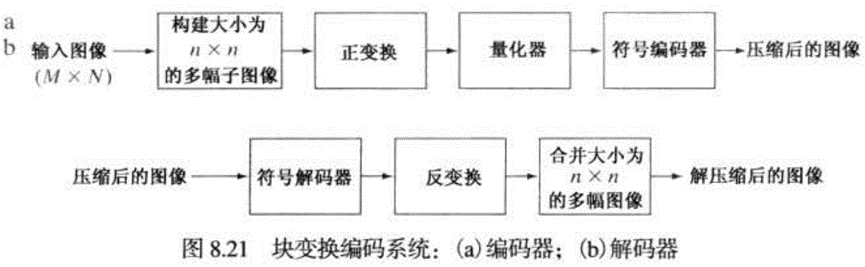
块变换编码

图像分成大小相等且不重叠的小块，并使用二维变换单独地处理这些块。 在块变换编码中，用一种可逆线性变换（如傅里叶变换）把每个块或子图像映射为变换系数集合，然后，对这些变换系数进量化和编码。

预测编码

它是通过消除紧邻像素在空间和时间上的冗余来实现的，它仅对每个像素中的新信息进行提取和编码。一个像素的新信息定义为该像素的实际值与预测值之间的差。

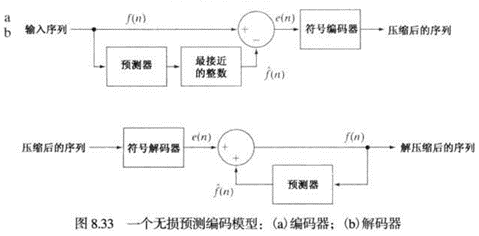
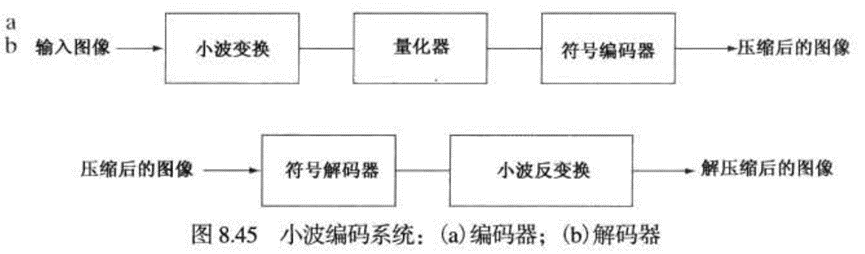
小波编码

对图像的像素解除相关的变换系数进行编码比对原图像像素本身进行编码的效率更高。

8.3 数字图像水印

令fw 代表水印的图像，我们可把它表示为未加水印图像f和水印 w 的如下线性组合：
$$f_w=(1－\alpha ）f＋\alpha w$$

常数α控制水印和衬底图像的相对可见性。如果α为1，则水印是不透明的，并且衬底图像完全是暗的。随着α接近0，会逐渐看到更多的衬底图像和更少的水印。

8.4小结

本章的主要介绍了数字图像压缩的理论基础，介绍了最常用的压缩方法，并介绍数字图像水印处理的相关领域。图像压缩，说到底就是对图像像素数据的排列组合的方式。不同的组合方式，在表达一幅图片时占据的空间不同。就起到了压缩的效果。所以要了解的是各种压缩方式的编码思路。