瞎聊机器学习——朴素贝叶斯以及拉普拉斯平滑

一、贝叶斯公式

贝叶斯公式是一种用来表示两个条件概率之间关系的公式，其具体表示如下：

公式中P(B|A)表示事件A发生的条件下事件B发生的概率，P(A|B)同理，P(A)、P(B)就表示事件A、B的概率，也就是像下面这样：

二、朴素贝叶斯

上面了解了贝叶斯公式，再来说说本文要讲的分类算法——朴素贝叶斯。

朴素贝叶斯是贝叶斯分类中最简单，也是最常见的算法，其中朴素一词的意思是假设各特征之间是相互独立的。

既然是分类算法我们就用分类的思想来表示贝叶斯公式：

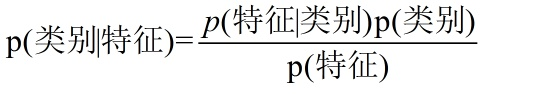
其中假设各个特征之间相互独立可以表示为：

 

P(特征|类别1，类别2，类别3) = p(特征|类别1)*p(特征|类别2)*p(特征|类别3)

 

我们最终要求得的结果也就是在某些特征下得到该类别的概率：P(类别|特征)

下面给出一个例子来说一下这个问题：

当我们去买西瓜的时候，我们并不知道哪个西瓜是熟瓜，此时我们就要想到通过什么条件能判断出西瓜是否成熟呢，我们给出一组经验数据作为参考：

	1	2	3	4	5	6	7	8	9	10
瓜蒂	脱落	未脱落	未脱落	脱落	脱落	未脱落	脱落	未脱落	脱落	未脱落
形状	圆形	尖形	圆形	尖形	圆形	尖形	尖形	圆形	尖形	圆形
颜色	深绿	浅绿	浅绿	青色	浅绿	青色	深绿	青色	浅绿	深绿
类别	瓜熟	瓜生	瓜生	瓜熟	瓜熟	瓜生	瓜熟	瓜熟	瓜生	瓜熟

根据数据表我们得到特征有：瓜蒂（脱落/未脱落）、形状（尖形/圆形）、颜色（深绿/浅绿/青色）

对于结果：不同的特征组合可以得到不同的结果（瓜熟/瓜生）

有了经验数据，对于不同特征的西瓜我们自然也就可以得到不同的判断结果，假定现在又一西瓜为（脱落、圆形、青色）：

对于上述的西瓜我们联系朴素贝叶斯公式得到：

p(瓜熟|脱落、圆形、青色)=p(脱落、圆形、青色|瓜熟) * p(瓜熟) / p(脱落、圆形、青色)

p(瓜生|脱落、圆形、青色)=p(脱落、圆形、青色|瓜生) * p(瓜生) / p(脱落、圆形、青色)

 

对于瓜熟的情况：

P(瓜熟) = 6 / 10 = 0.6

P(脱落 | 瓜熟) = 4 / 6 = 2 / 3

P(圆形 | 瓜熟) = 4 / 6 = 2 / 3

P(青色 | 瓜熟) = 2 / 6 = 1 / 3

 

对于瓜生的情况：

P(瓜生) = 4 / 10 = 0.4

P(脱落 | 瓜生) = 1 / 4 = 0.25

P(圆形 | 瓜生) = 1 / 4 = 0.25

P(青色 | 瓜生) = 1 / 4 = 0.25

 

对于如何判断瓜熟还是瓜生，我们比较p(瓜熟|脱落、圆形、青色)和p(瓜生|脱落、圆形、青色)的概率就可以了：

因为二者的贝叶斯公式中都存在相同的p(脱落、圆形、青色)所以我们只需要比较p(脱落、圆形、青色|瓜熟)*p(瓜熟)和p(脱落、圆形、青色|瓜生)*p(瓜生)：

我们假设各个特征之间相互独立：

P(瓜熟) × P(脱落 | 瓜熟) × P(圆形 | 瓜熟) × P(青色 | 瓜熟) = 0.6 × (2 / 3) × (2 / 3) × (1 / 3) = 4 / 45

P(瓜生) × P(脱落 | 瓜生) × P(圆形 | 瓜生) × P(青色 | 瓜生) = 0.4 × 0.25 × 0.25 × 0.25 = 1 / 160

比较一下：4/45>1/160，所以我们预测该西瓜为瓜熟。

通过该例子，我们就能够大致了解朴素贝叶斯的工作原理以及计算方法，下面通过sklearn和iris数据集来简单的实践一下：

from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score
from sklearn import datasets

iris = datasets.load_iris()
gnb = GaussianNB()
scores = cross_val_score(gnb, iris.data, iris.target, cv=10)
print("Accuracy:%.3f" % scores.mean())

得到的结果如下：

三、拉普拉斯平滑

对于某个数据集，我们考虑到对于某个特征X在训练集中没有出现，那么将会导致整个分类概率变为0，这将会导致分类变得非常不合理，所以为了解决零概率的问题，法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率，所以加法平滑也叫做拉普拉斯平滑。假定训练样本很大时，每个分量x的计数加1造成的估计概率变化可以忽略不计，但可以方便有效的避免零概率问题。

应用举例：

假设在文本分类中，有3个类，C1、C2、C3，在指定的1000个训练样本中，某个词语K1，在各个类中观测计数分别为0，990，10，K1的概率为0，0.99，0.01。

对这三个量使用拉普拉斯平滑的计算方法如下：

，，

在实际的使用中也经常使用加 lambda（1≥lambda≥0）来代替简单加1。如果对N个计数都加上lambda，这时分母也要记得加上N*lambda。