1. 傅里叶级数FS
任何周期信号都可以表示为若干个正弦函数和余弦函数之和:
f
(
t
)
=
a
0
+
∑
0
∞
(
a
n
c
o
s
(
2
π
n
t
T
)
+
b
n
s
i
n
(
2
π
n
t
T
)
)
f(t) = a_0 + \sum^{\infty}_0(a_ncos(\frac{2\pi nt}{T}) + b_nsin(\frac{2\pi nt}{T}))\\
f(t)=a0+0∑∞(ancos(T2πnt)+bnsin(T2πnt))
其中
a
0
=
1
T
∫
0
T
f
(
t
)
d
t
a_{0}=\frac{1}{T} \int_{0}^{T} f(t) d t
a0=T1∫0Tf(t)dt,
a
n
=
2
T
∫
0
T
f
(
t
)
cos
(
2
π
n
t
T
)
d
t
a_{n}=\frac{2}{T} \int_{0}^{T} f(t) \cos \left(\frac{2 \pi n t}{T}\right) d t
an=T2∫0Tf(t)cos(T2πnt)dt,
b
n
=
2
T
∫
0
T
f
(
t
)
sin
(
2
π
n
t
T
)
d
t
b_{n}=\frac{2}{T} \int_{0}^{T} f(t) \sin \left(\frac{2 \pi n t}{T}\right) d t
bn=T2∫0Tf(t)sin(T2πnt)dt。
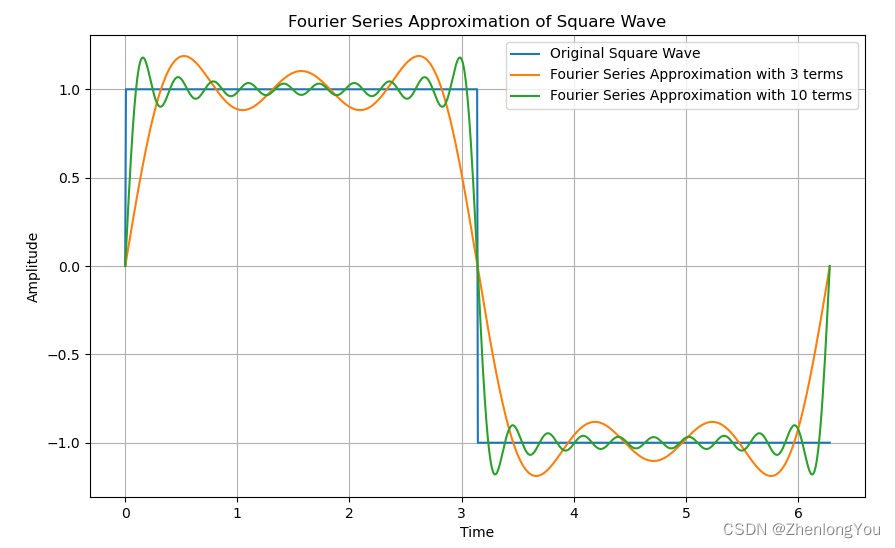
例子: 假设我们有一个周期为T的方波信号f(t):
f
(
t
)
=
A
,
0
≤
t
≤
T
2
f
(
t
)
=
−
A
,
T
2
≤
t
≤
T
f(t) = A, 0\leq t \le \frac{T}{2} \\ f(t) = -A, \frac{T}{2} \leq t \le T
f(t)=A,0≤t≤2Tf(t)=−A,2T≤t≤T
因为方波为奇函数,所以只存在奇数次谐波的正弦项
b
n
b_n
bn:
b
n
=
2
T
(
∫
0
T
/
2
A
sin
(
2
π
n
t
T
)
d
t
+
∫
T
/
2
T
−
A
sin
(
2
π
n
t
T
)
d
t
)
b_{n}=\frac{2}{T}\left(\int_{0}^{T / 2} A \sin \left(\frac{2 \pi n t}{T}\right) d t+\int_{T / 2}^{T}-A \sin \left(\frac{2 \pi n t}{T}\right) d t\right)
bn=T2(∫0T/2Asin(T2πnt)dt+∫T/2T−Asin(T2πnt)dt)
将这些系数带入傅里叶级数公式中,我们可以得到方波信号的傅里叶级数展开形式:
f
(
t
)
=
∑
k
=
0
∞
4
A
(
2
k
+
1
)
π
sin
(
2
π
(
2
k
+
1
)
t
T
)
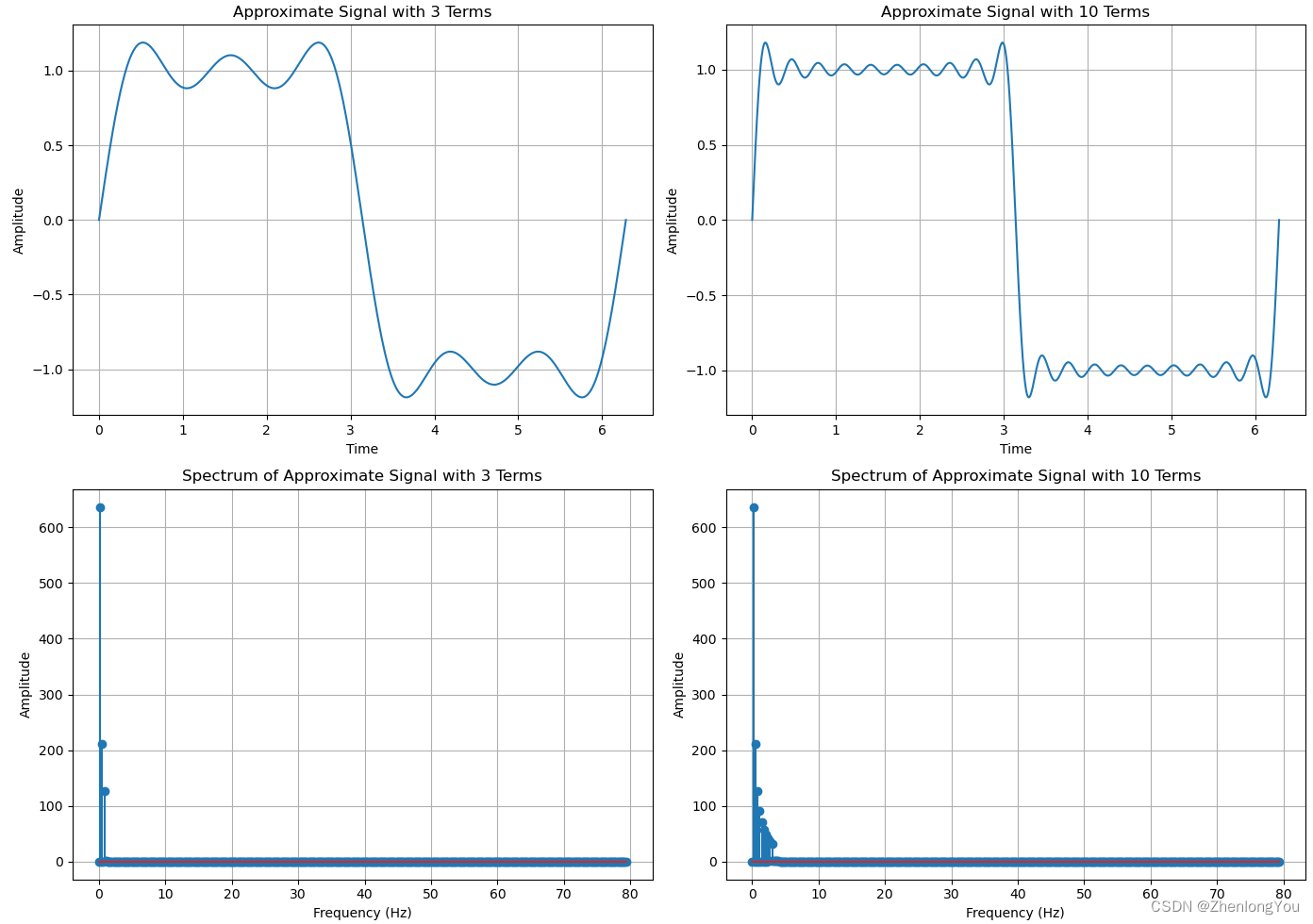
f(t) = \sum_{k=0}^{\infty} \frac{4A}{(2k+1)\pi} \sin \left( \frac{2\pi(2k+1)t}{T} \right)
f(t)=k=0∑∞(2k+1)π4Asin(T2π(2k+1)t)
f
(
t
)
=
a
0
2
+
∑
n
=
1
∞
(
a
n
cos
n
ω
t
+
b
n
sin
n
ω
t
)
f
(
t
)
=
a
0
2
+
∑
n
=
1
∞
[
a
n
⋅
1
2
(
e
i
n
ω
t
+
e
−
i
n
ω
t
)
−
1
2
i
b
n
(
e
i
n
ω
t
−
e
−
i
n
ω
t
)
]
f
(
t
)
=
∑
−
∞
∞
C
n
e
i
n
ω
t
f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( a_n \cos n\omega t + b_n \sin n\omega t \right)\\ f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left[ a_n \cdot \frac{1}{2} \left( e^{i n \omega t} + e^{-i n \omega t} \right) - \frac{1}{2i} b_n \left( e^{i n \omega t} - e^{-i n \omega t} \right) \right]\\ f(t) = \sum^{\infty}_{-\infty}C_ne^{in\omega t}
f(t)=2a0+n=1∑∞(ancosnωt+bnsinnωt)f(t)=2a0+n=1∑∞[an⋅21(einωt+e−inωt)−2i1bn(einωt−e−inωt)]f(t)=−∞∑∞Cneinωt
其中
C
n
C_n
Cn表示为:
C
n
=
a
0
2
,
n
=
0
C
n
=
a
n
−
i
b
n
2
,
n
=
1
,
2
,
3
,
4
,
…
C
n
=
a
n
+
i
b
n
2
,
n
=
−
1
,
−
2
,
−
3
,
−
4
,
…
C_n = \frac{a_0}{2}, n = 0 \\ C_n =\frac{a_n - i b_n}{2}, n = 1, 2, 3, 4, \ldots \\ C_n =\frac{a_n + i b_n}{2}, n = -1, -2, -3, -4, \ldots
Cn=2a0,n=0Cn=2an−ibn,n=1,2,3,4,…Cn=2an+ibn,n=−1,−2,−3,−4,…
所以周期信号
f
(
t
)
=
f
(
t
+
T
)
f(t) = f(t + T)
f(t)=f(t+T)的傅里叶级数可以总结为:
f
(
t
)
=
∑
n
=
−
∞
∞
C
n
e
i
n
ω
t
C
n
=
1
T
∫
0
T
f
(
t
)
e
−
i
n
ω
t
d
t
f(t) = \sum_{n=-\infty}^{\infty} C_n e^{i n \omega t}\\ C_n = \frac{1}{T} \int_{0}^{T} f(t) e^{-i n \omega t} \, dt
f(t)=n=−∞∑∞CneinωtCn=T1∫0Tf(t)e−inωtdt
2. 傅里叶变换FT
当信号为非周期信号时,即傅里叶级数中的T趋近于无穷大时,傅里叶级数可视为傅里叶变换
lim
T
→
∞
f
T
(
t
)
=
f
(
t
)
f
T
(
t
)
=
f
(
t
+
T
)
f
T
(
t
)
=
∑
n
=
−
∞
∞
C
n
e
i
n
ω
0
t
\lim_{T \to \infty} f_T(t) = f(t)\\ f_T(t) = f(t + T)\\ f_T(t) = \sum_{n=-\infty}^{\infty} C_n e^{i n \omega_0 t}
T→∞limfT(t)=f(t)fT(t)=f(t+T)fT(t)=n=−∞∑∞Cneinω0t
在傅里叶级数中
ω
0
=
2
π
T
\omega_0 = \frac{2\pi}{T}
ω0=T2π
Δ
ω
=
(
n
+
1
)
ω
0
−
n
ω
0
=
ω
0
=
2
π
T
\Delta \omega = (n+1)\omega_0 - n\omega_0 = \omega_0 = \frac{2\pi}{T}
Δω=(n+1)ω0−nω0=ω0=T2π
1
T
=
Δ
ω
2
π
\frac{1}{T} = \frac{\Delta \omega}{2\pi}
T1=2πΔω, 当
T
↑
,
Δ
ω
↓
T \uparrow, \Delta \omega \downarrow
T↑,Δω↓,则
Δ
ω
\Delta \omega
Δω逐渐由离散趋近于连续。
f
T
(
t
)
=
∑
n
=
−
∞
∞
(
1
T
∫
−
2
T
2
T
f
T
(
t
)
e
−
i
n
ω
0
t
d
t
)
e
i
n
ω
0
t
→
f
T
(
t
)
=
f
T
(
t
)
=
∑
n
=
−
∞
∞
Δ
ω
2
π
∫
−
T
2
T
2
f
T
(
t
)
e
−
i
n
ω
0
t
d
t
e
i
n
ω
0
t
f_T(t) = \sum_{n=-\infty}^{\infty} \left( \frac{1}{T} \int_{-\frac{2}{T}}^{\frac{2}{T}} f_T(t) e^{-i n \omega_0 t} dt \right) e^{i n \omega_0 t} \rightarrow f_T(t) = f_T(t) = \sum_{n=-\infty}^{\infty} \frac{\Delta \omega}{2\pi} \int_{-\frac{T}{2}}^{\frac{T}{2}} f_T(t) e^{-i n \omega_0 t} \, dt \, e^{i n \omega_0 t}
fT(t)=n=−∞∑∞(T1∫−T2T2fT(t)e−inω0tdt)einω0t→fT(t)=fT(t)=n=−∞∑∞2πΔω∫−2T2TfT(t)e−inω0tdteinω0t
当
T
→
∞
:
∫
−
T
2
T
2
d
t
→
∫
−
∞
∞
d
t
,
n
ω
0
→
ω
:
∑
n
=
−
∞
∞
Δ
ω
→
∫
−
∞
∞
d
ω
T \to \infty: \int_{-\frac{T}{2}}^{\frac{T}{2}} dt \to \int_{-\infty}^{\infty} dt, \\n \omega_0 \to \omega: \sum_{n=-\infty}^{\infty} \Delta \omega \to \int_{-\infty}^{\infty} d\omega
T→∞:∫−2T2Tdt→∫−∞∞dt,nω0→ω:∑n=−∞∞Δω→∫−∞∞dω。
所以:
f
T
(
t
)
=
∑
n
=
−
∞
∞
Δ
ω
2
π
∫
−
T
2
T
2
f
T
(
t
)
e
−
i
n
ω
t
d
t
e
i
n
ω
t
→
f
(
t
)
=
1
2
π
∫
−
∞
∞
(
∫
−
∞
∞
f
(
t
)
e
−
i
ω
t
d
t
)
e
i
ω
t
d
ω
f_T(t) = \sum_{n=-\infty}^{\infty} \frac{\Delta \omega}{2\pi} \int_{-\frac{T}{2}}^{\frac{T}{2}} f_T(t) e^{-i n \omega t} \, dt \, e^{i n \omega t} \rightarrow f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \left( \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt \right) e^{i \omega t} \, d\omega
fT(t)=n=−∞∑∞2πΔω∫−2T2TfT(t)e−inωtdteinωt→f(t)=2π1∫−∞∞(∫−∞∞f(t)e−iωtdt)eiωtdω
傅里叶变换表达式推导为:
F
(
ω
)
=
∫
−
∞
∞
f
(
t
)
e
−
i
ω
t
d
t
f
(
t
)
=
1
2
π
∫
−
∞
∞
F
(
ω
)
e
i
ω
t
d
ω
F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt\\ f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} \, d\omega
F(ω)=∫−∞∞f(t)e−iωtdtf(t)=2π1∫−∞∞F(ω)eiωtdω
3. 离散时间傅里叶变换DTFT
DTFT为FT的离散情况(DTFT可视为z变换在单位圆上的值),对FT原本连续的时域信号以
Δ
t
\Delta t
Δt为步进进行取样:
F
(
ω
)
=
∫
−
∞
∞
f
(
t
)
e
−
i
ω
t
d
t
→
∑
−
∞
∞
f
[
n
]
e
−
i
ω
n
F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt \rightarrow \sum^{\infty}_{-\infty}f[n]e^{-i \omega n}
F(ω)=∫−∞∞f(t)e−iωtdt→−∞∑∞f[n]e−iωn
1.
t
→
n
2.
∫
−
∞
∞
d
t
→
∑
n
=
−
∞
∞
3.
e
−
i
ω
t
→
e
−
i
n
ω
t
(
Δ
t
=
1
)
→
e
i
n
ω
1. \quad t \to n \\ 2. \quad \int_{-\infty}^{\infty} dt \to \sum_{n=-\infty}^{\infty} \\ 3. \quad e^{-i \omega t} \to e^{-i n \omega t} \quad (\Delta t = 1) \rightarrow e^{i n \omega}
1.t→n2.∫−∞∞dt→∑n=−∞∞3.e−iωt→e−inωt(Δt=1)→einω
详细转换过程如下:

x
s
(
t
)
=
x
c
(
t
)
⋅
∑
k
=
−
∞
∞
δ
(
t
−
k
T
)
=
∑
k
=
−
∞
∞
x
c
(
k
T
)
⋅
δ
(
t
−
k
T
)
x_s(t) = x_c(t) \cdot \sum_{k=-\infty}^{\infty} \delta(t - kT) = \sum_{k=-\infty}^{\infty} x_c(kT) \cdot \delta(t - kT)
xs(t)=xc(t)⋅k=−∞∑∞δ(t−kT)=k=−∞∑∞xc(kT)⋅δ(t−kT)
∑
k
=
−
∞
∞
δ
(
t
−
k
T
)
⟷
F
2
π
T
∑
n
=
−
∞
∞
δ
(
ω
−
2
π
T
n
)
\sum_{k=-\infty}^{\infty} \delta(t - kT) \overset{\mathcal{F}}{\longleftrightarrow} \frac{2\pi}{T} \sum_{n=-\infty}^{\infty} \delta \left( \omega - \frac{2\pi}{T} n \right)
k=−∞∑∞δ(t−kT)⟷FT2πn=−∞∑∞δ(ω−T2πn)
X
s
(
j
ω
)
=
1
2
π
X
c
(
j
ω
)
∗
2
π
T
∑
n
=
−
∞
∞
δ
(
ω
−
2
π
T
n
)
=
1
T
∑
n
=
−
∞
∞
X
c
(
j
[
ω
−
2
π
T
n
]
)
X_s(j\omega) = \frac{1}{2\pi} X_c(j\omega) * \frac{2\pi}{T} \sum_{n=-\infty}^{\infty} \delta \left( \omega - \frac{2\pi}{T} n \right) = \frac{1}{T} \sum_{n=-\infty}^{\infty} X_c \left( j \left[ \omega - \frac{2\pi}{T} n \right] \right)
Xs(jω)=2π1Xc(jω)∗T2πn=−∞∑∞δ(ω−T2πn)=T1n=−∞∑∞Xc(j[ω−T2πn])
所以对FT进行采样后,信号频谱以fs为周期重复,信号频谱幅度变为原有的
1
T
\frac{1}{T}
T1, 且采样频率fs需要大于原有信号频谱宽度
f
b
f_b
fb两倍,即满足奈奎斯特采样定理。
此时时域信号是离散的,但在频域上通过DTFT变换得到的频谱是一个连续的周期性函数。这种连续的频谱对于实际的计算机处理来说是一个挑战,因为计算机只能处理离散的数值数据。为了在计算机上进行处理,通常会使用离散傅里叶变换(DFT),这是对DTFT的一个离散化和有限化的版本。DFT在频域上生成离散的频谱,这样就可以在计算机上处理。这也是快速傅里叶变换(FFT)算法的基础,FFT算法可以高效地计算DFT。
4. 离散傅里叶级数DFS
将DTFT中离散非周期的时域信号拓展为周期信号再做傅里叶变换即为DFS:
x
~
(
n
)
=
x
~
(
n
+
r
N
)
\tilde{x}(n) = \tilde{x}(n + rN)
x~(n)=x~(n+rN)
FS:
f
(
t
)
=
∑
n
=
−
∞
∞
C
n
e
i
n
ω
t
C
n
=
1
T
∫
0
T
f
(
t
)
e
−
i
n
ω
t
d
t
f(t) = \sum_{n=-\infty}^{\infty} C_n e^{i n \omega t}\\ C_n = \frac{1}{T} \int_{0}^{T} f(t) e^{-i n \omega t} \, dt
f(t)=n=−∞∑∞CneinωtCn=T1∫0Tf(t)e−inωtdt
将
C
n
C_n
Cn代入
f
(
t
)
f(t)
f(t):
f
(
t
)
=
∑
n
=
−
∞
∞
(
1
T
∫
0
T
f
(
t
)
e
−
i
n
ω
t
d
t
)
e
i
n
ω
t
f(t) = \sum_{n=-\infty}^{\infty} \left( \frac{1}{T} \int_{0}^{T} f(t) e^{-i n \omega t} \, dt \right) e^{i n \omega t}
f(t)=n=−∞∑∞(T1∫0Tf(t)e−inωtdt)einωt
因为DFS的时域信号相较于FS变为离散周期信号,所以:
1.
t
→
n
2.
T
→
N
3.
x
^
(
t
)
→
x
^
[
n
]
4.
e
i
2
π
T
n
t
→
e
i
2
π
N
n
k
1.\ t \to n \\ 2.\ T \to N \\ 3.\ \hat{x}(t) \to \hat{x}[n] \\ 4.\ e^{i \frac{2\pi}{T} n t} \to e^{i \frac{2\pi}{N} n k}
1. t→n2. T→N3. x^(t)→x^[n]4. eiT2πnt→eiN2πnk
f
(
n
)
=
∑
n
=
−
∞
∞
1
N
∑
n
=
0
N
−
1
f
(
n
)
e
−
i
2
π
N
k
n
⋅
e
i
2
π
N
k
n
f(n)=\sum_{n=-\infty}^{\infty} \frac{1}{N} \sum_{n=0}^{N-1} f(n) e^{-i \frac{2\pi}{N} k n} \cdot e^{i \frac{2\pi}{N} k n}
f(n)=n=−∞∑∞N1n=0∑N−1f(n)e−iN2πkn⋅eiN2πkn
DFS:
X
~
(
k
)
=
∑
n
=
0
N
−
1
x
~
(
n
)
e
−
j
2
π
N
k
n
x
~
(
n
)
=
1
N
∑
k
=
0
N
−
1
X
~
(
k
)
e
j
2
π
N
k
n
\tilde{X}(k) = \sum_{n=0}^{N-1} \tilde{x}(n) e^{-j \frac{2\pi}{N} k n}\\ \tilde{x}(n) = \frac{1}{N} \sum_{k=0}^{N-1} \tilde{X}(k) e^{j \frac{2\pi}{N} k n}
X~(k)=n=0∑N−1x~(n)e−jN2πknx~(n)=N1k=0∑N−1X~(k)ejN2πkn
5. 离散傅里叶变换DFT
DFT为DFS第一个周期的DFS:
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
e
−
j
2
π
N
k
n
x
(
n
)
=
1
N
∑
k
=
0
N
−
1
X
(
k
)
e
j
2
π
N
k
n
{X}(k) = \sum_{n=0}^{N-1} {x}(n) e^{-j \frac{2\pi}{N} k n}\\ {x}(n) = \frac{1}{N} \sum_{k=0}^{N-1} {X}(k) e^{j \frac{2\pi}{N} k n}
X(k)=n=0∑N−1x(n)e−jN2πknx(n)=N1k=0∑N−1X(k)ejN2πkn
各类型傅里叶变换示意图如下: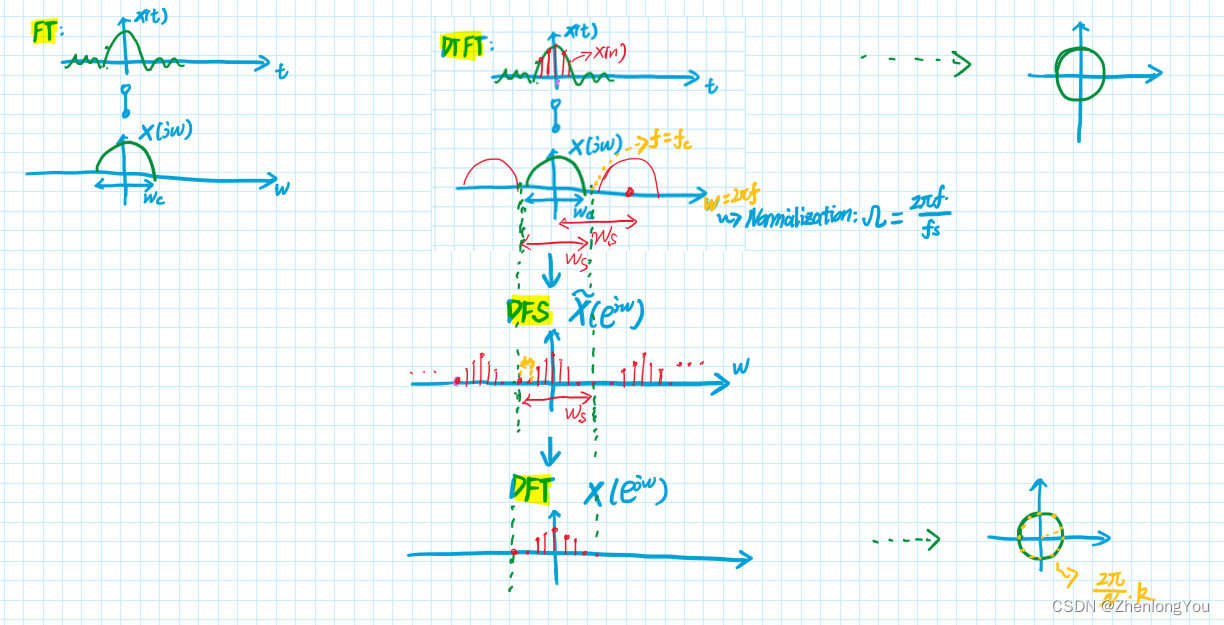





















 6465
6465

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








