《博弈论》笔记

《博弈论》笔记

- 默认“1”，“i”，“①”为第一视角思考
- 前部分所说纳什均衡指“纯策略纳什均衡”
- “ε”表示无穷小的一个数
- ES：进化稳定性
- 混合策略不可能严格

---

[原则]

• 不要选严格劣势策略
• 理性的选择导致次优结果
• 如欲得之，必先知之
• 换位思考
• 人人自私，考虑非理性因素

---

“博弈”组成：

i,j······	参与人
si	i的某策略
Si	i的策略合集
S	某次博弈(即多个策略组合参与)
Ui(s1,···,sn) <=> Ui(S)	i的收益
S¬i <=>S(s1,···,sn)除si	除i外的策略合集

Famp.

1\2	L	C	R
T	5,-1	11,3	0,0
B	6,4	0,2	2,0

• 参与人：
  • 1
  • 2
• 策略收益：
  • S1 = { T , B }
  • S2 = { L , C , R }
• 收益：
  • U1（ T , C ）=11
  • U2（ T , C ）=3

---

严格优势策略

Def.

• i的策略si严格优于i的另一策略s‘i;在其他人选S¬i时，Ui(si)严格优于此情况下选s’i的收益Ui(s‘i)
• 对所有s¬i成立时才称为优势
• 优势利益时针对自己的利益而言，不用考虑对方的利益得失

---

弱劣势策略

Def.

• 原本不是劣势策略，多次换位思考并剔除劣势策略的结果。
• i的策略s’i弱劣于其他策略si当且仅当
  • Ui（si,s¬i）>= Ui(s’i,s¬i)在任何情况均成立，
  • Ui（si,s¬i）> Ui(s’i.s¬i)至少一种情况成立。

---

迭代剔除劣势策略

Famp.中间立场选民定理

• 参与人：2位候选人
• 策略：
  • 共十个立场：1-10且1与10不相邻
  • 每个立场都有10%的选民
• 收益：最大化得票
• rule：
  • 票民会投给最近的候选人
  • 10%均分：5% <— 10% —>5%

【思考1】：立场1，立场2谁有优势？

• U1(1,1) = 50% < U1(2,1) = 90%
• U1(1,2) = 10% < U1(2,1) = 50%
• U1(1,3) = 15% < U1(2,1) = 20%
• U1(1,4) = 20% < U1(2,1) = 25%······

所以，立场2严格优于立场1

同理，立场9严格优于立场10

【思考2】：立场2是否严格劣于立场3？

• U1(2,1) = 90% < U1(3,1) = 85%

所以，立场2不是严格劣于立场3

【思考3】：如果剔除劣势策略1，10，那么【思考2】成立吗？

• U1(2,2) = 50% < U1(3,2) = 80%
• U1(2,3) = 20% < U1(3,3) = 50%
• U1(2,4) = 25% < U1(3,4) = 35%···

所以，在剔除劣势策略后，【思考2】成立

【总结与思考】

• 立场2，立场9本不是严格劣势策略；但无人选1，10的话，立场2和9会变为严格劣势策略。所以2，9这种为弱劣势策略
• 如果进行多次迭代剔除劣势策略（2和9，3和8，4和7）后，最终只剩5和6.即应选用的策略为立场5和6.
• 该模型忽略了诸多因素，利于理解即可

---

最佳对策

Def.

• 如果Ui(s^i,s¬i) >= Ui(si,s¬i)恒成立，或者Ui(si,s¬i)max时，si = s^i.则说明si是i的最佳对策

Famp.

1\2	l	r
u	5,1	0,2
m	1,3	4,1
d	4,2	2,3

【分析】：对于2来讲，策略l和r的收益相同，可以预测2选l或r的概率均为50%；此时1的哥哥策略收益期望为：

• U1(u,s2) = 5 * 0.5 + 0* 0.5 = 2.5
• U1(m,s2) = 1 * 0.5 + 4* 0.5 = 2.5
• U1(d,s2) = 4 * 0.5 + 2* 0.5 = 3

所以，选 d 应为 1 的最佳策略 （期望值最大）

【变式】：如果2号选择策略l，r的概率不是0.5，那么应该如何选择最佳对策？

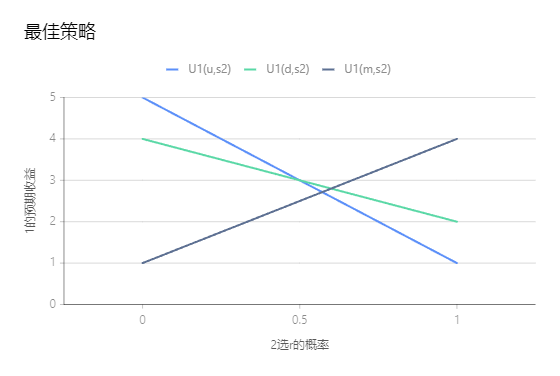
• 最上方部分的线段组合即为：最佳策略
• 很明显，要想选到最佳对策需要知道对方的真实想法，而这便是最难的

---

合作人博弈

Famp.

• 参与人：1，2
• 策略：S∈[ 0 , 4 ] //投入的精力
• 利益和：4 * （s1 + s2 + bs1*s2）
• rule：利益均分
• 1的利益U1(s1,s2) = 0.5 * 4 * （s1 + s2 + bs1*s2）- s1^2
• 2的利益U2(s1,s2) = 0.5 * 4 * （s1 + s2 + bs1*s2）- s2^2

【思考1】：1的最佳策略

U1 = 2(s1 + s2 + bs1*s2) - s1^2
(U1)' = 2 + 2bs2 - 2s1		//求导
令(U1)' = 0 
得s1 = 1 + bs2
所以，此时 S^1 = s1 为最佳策略

• 对于1而言[ 1 , 2 ]为最佳策略

• 对于1而言[ 1 , 2 ]为最佳策略

• 剔除劣势策略后，保留最佳部分（红色阴影部分）

放大最优部分图

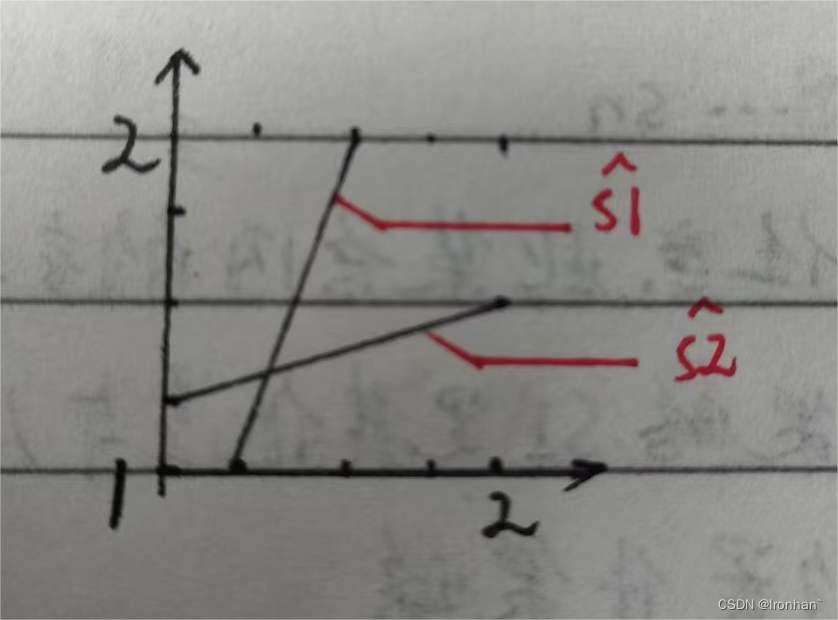
• 此时产生了弱劣势策略，可再次剔除
• 最终应汇聚于交点,即：

s^1 = 1 + bs^2
s^2 = 1 + bs^1
s^1 = s^2
所以，s^1 = s^2 = 1/(1-b),即交点最佳策略

• 该交点为【纳什均衡】：参与人都采取了各自最佳策略的结果。

---

纳什均衡

Def.

• 集合A包含每个参与人的一个已选策略：s1,···，sn
• 满足：对于任意此集合内的参与人i，其所选策略si时其他参与人所选策略s¬i的最佳策略
• 使用动机：
  • 不后悔：其他参与人不改变行为的前提下，自己改变
  • 自我实施的预测：只有这种情况，双方都不后悔

Famp.找纳什均衡

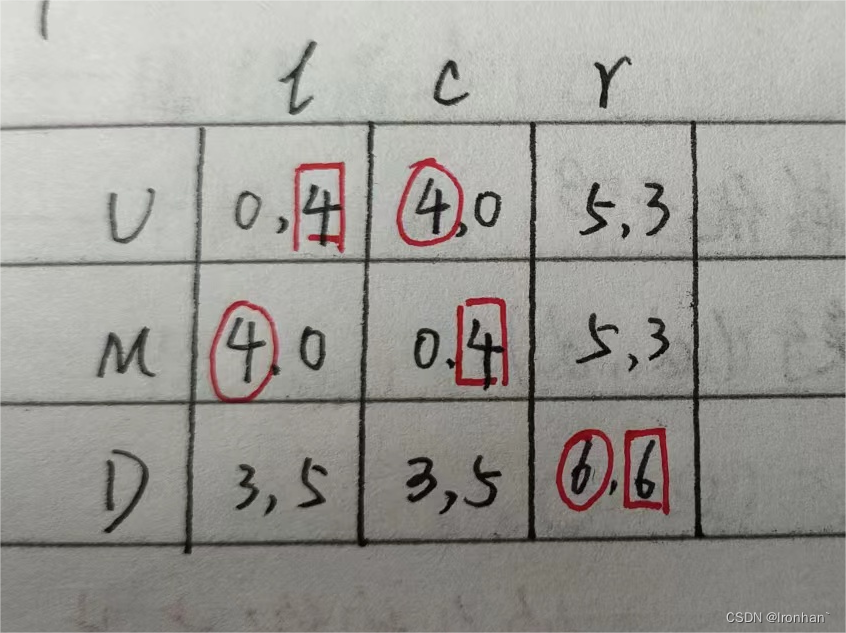
BR1(l) = M			BR2(U) = l
BR1(c) = U			BR2(M) = c
BR1(r) = D			BR2(D) = r
[^B]：Best.最优解

• 纳什均衡一定是双方最优解：( D ， r )

---

纳什均衡与优劣势策略

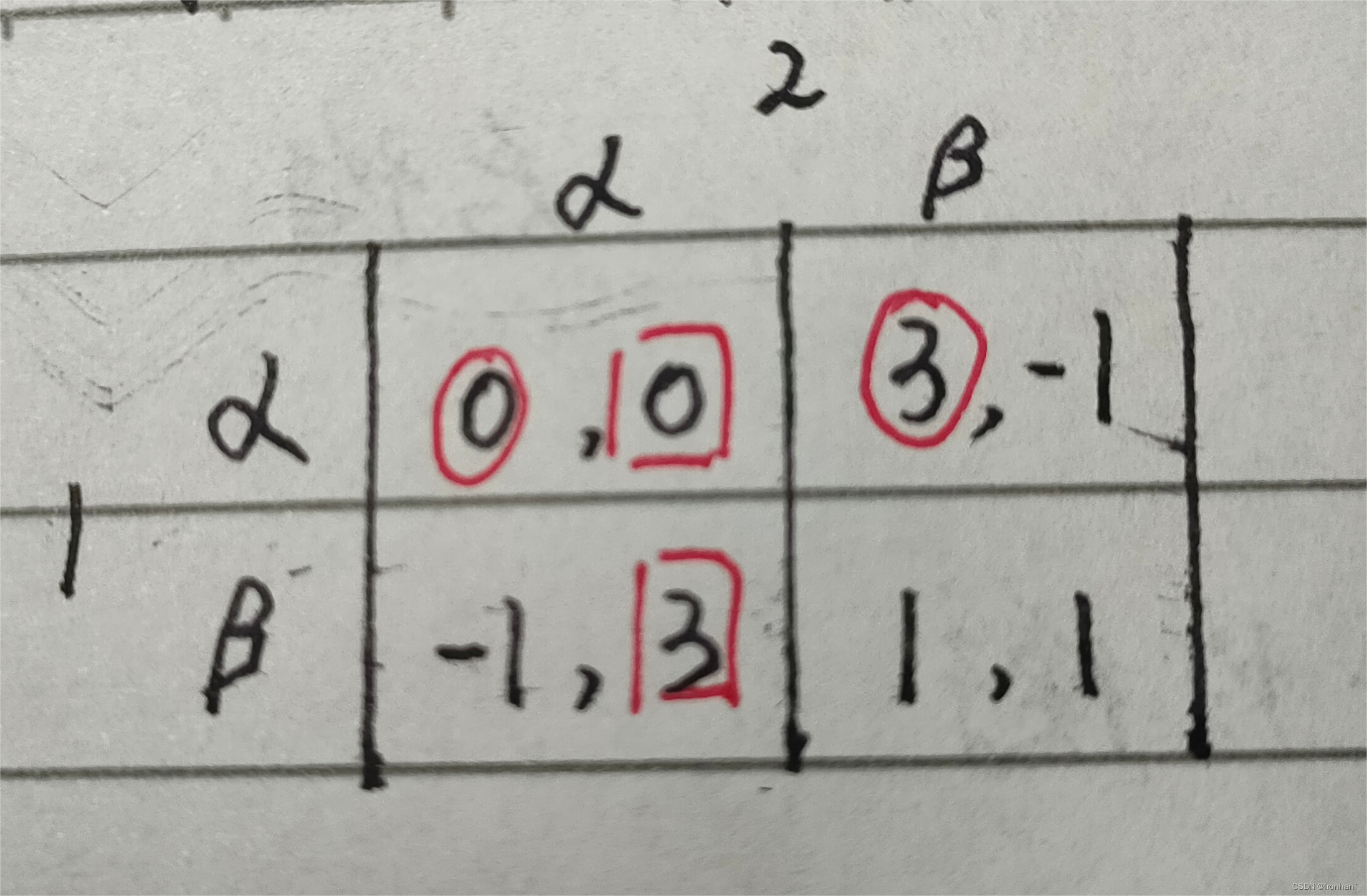
• α严格优于β
• 纳什均衡为( α , α )

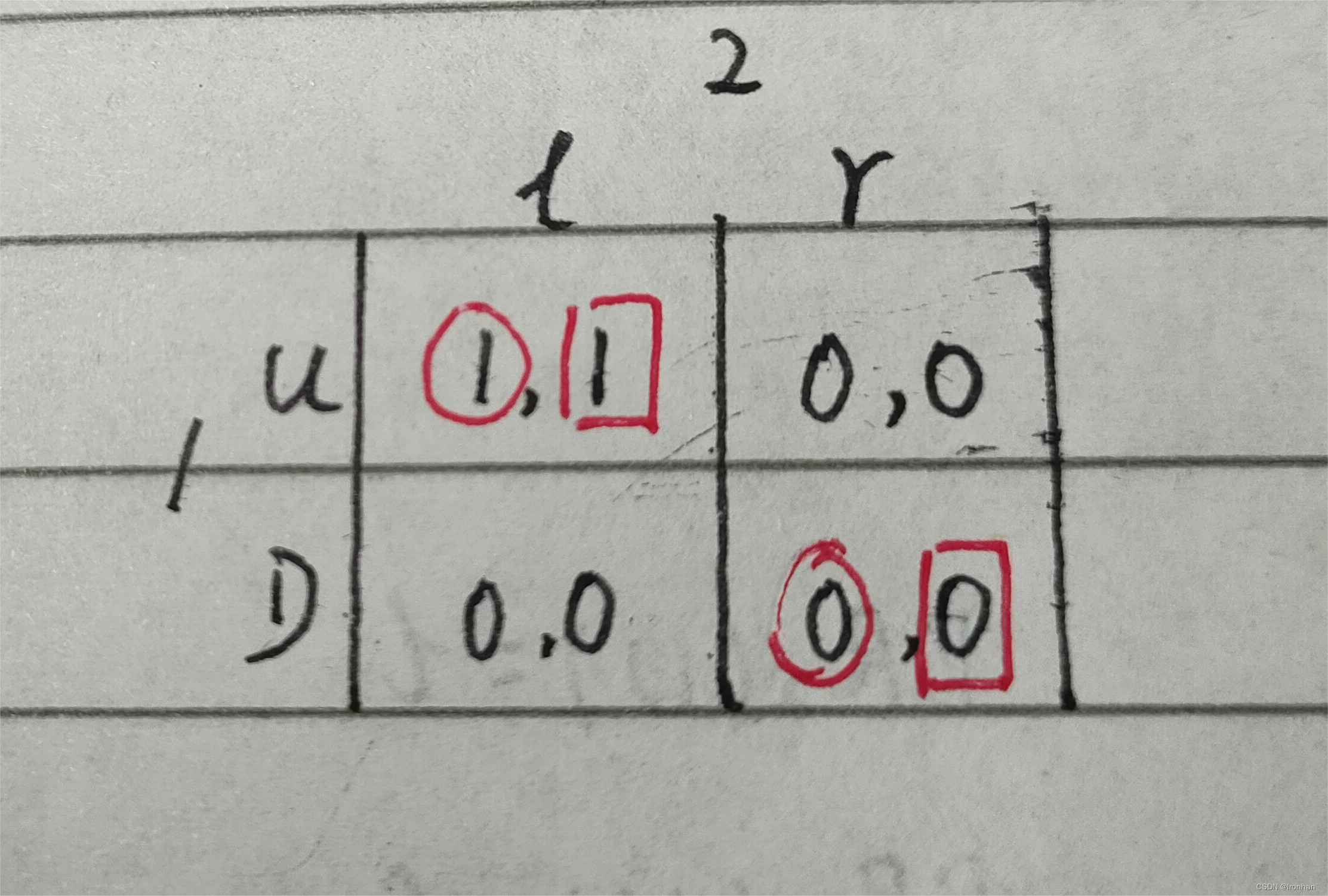
• 纳什均衡有时不止一个

---

古诺双寡头

Famp.古诺双寡头(产量)

---

伯川德竞争

Fmap.伯川德竞争(价格)

• 参与人：公司1、公司2

• 策略：价格P,P1,P2 //0 < P <1

• 产量：Q§ = 1 - P //市场总产量

• 公司1产量：Q1=

  • 1 - P1 (P1 < P2)
  • 0 (P1 > P2)
  • (1 - P1) / 2 (P1 = P2)

• 利益：U1 = Q1 ( P1 - C )

• rule：利益最大化，定价低者得全部市场

BR1(P1) = ① P1 > P2		//P2 < C
		  ② P1 = P2 - ε 	//ε足够小，C < P2 <= P垄断
          ③ P垄断		   //C < P垄断 < P2
          ④ P1 >= C		//P2 = C
---
[^①，④]：这是一个避免损失的策略，如果一家公司定价低于成本，我还想卖出产品，那么我的唯一方法时定价比他低；但每卖出一件产品，我就要承担一份亏损；不想承担亏损，就要推出市场，于是定价要高点。
---
纳什均衡（完全竞争）：两家公司价格定在成本C。（无利益）

---

混合策略（Pi）

Def.

• Pi：纯策略的概率
• Pi(si)：在混合策略Pi下参与人i采用策略si的概率
• Pi(si)中的si可为0
• Pi(si)中的si可为1（赋予一个策略概率为1）
• 收益：每个纯策略预期收益的加权平均数

Famp.1

	石头	剪刀	布
石头	0，0	1，-1	-1，1
剪刀	-1，1	0，0	1，-1
布	1，-1	-1，1	0，0

• 无纯策略纳什均衡
• 纳什均衡：每个参与者以1/3的概率选择的混合策略
• 混合策略预期收益：0

Famp.2

1\2	A	B
A	2,1	0,0
B	0,0	1,2

• 假设：
  • 1的混合策略概率：P = （0.2，0.8）
  • 2的混合策略概率：Q = （0.5，0.5）
• 1的预期收益 =
  • EU1(A,Q) = 2 * 0.5 + 0 * 0.5 = 1
  • EU1(B,Q) = 0 * 0.5 + 1 * 0.5 = 0.5
  • EU1(P,Q) = EU1(A,Q) * PA + EU1(B,Q) * PB =1 * 0.2 + 0.5 * 0.8 = 0.6

【补充】

• 如果一个混合策略时最佳对策；那么，混合策略中的每个纯策略一定也是最佳对策；也就是说，其中每个纯策略的预期收益相同。

famp.3

求混合策略纳什均衡概率

• 不存在纯策略纳什均衡，存在混合策略纳什均衡

Uv :  L:50 * q + 80 * (1-q)
	  R:90 * q + 20 * (1-q)
   ∵  处于纳什均衡状态
   ∴  L = R
   ∴  q = 0.6
   ∴  v的混合策略纳什均衡（0.6，0.4）
Us :  l:50 * p + 10 * (1-p)
	  r:20 * p + 80 * (1-p)
   ∵  l = r
   ∴  p = 0.7
∴s的混合策略纳什均衡为（0.7，0.3）

• 验证混合策略纳什均衡是否为最佳策略：只需验证仅选纯策略时是否更有利益；包括没选的纯策略。

famp.4 性别大战

是否存在混合策略纳什均衡?

• 两个纯策略纳什均衡

U1(A) = 2 * Q + 0 * (1-Q)
U1(B) = 0 * Q + 1 * (1-Q)
令 U1(A) = U1(B)
∴ Q = 1/3
∴ 1的混合策略纳什均衡为(1/3,2/3)
U2(A) = 1 * P + 0 * (1-P)
U2(B) = 0 * P + 2 * (1-P)
令 U2(A) = U2(B)
∴ P = 2/3
∴ 2的混合策略纳什均衡为(2/3,1/3)

Famp.4 税收

求混合策略纳什均衡

• 不存在纯策略纳什均衡

U1(A) = 2 * Q + 4 * (1-Q)
U1(B) = 4 * Q + 0 * (1-Q)
U1(A) = U1(B)
∴ Q = 2/3
即1混合策略纳什均衡（2/3，1/3）
U2(C) = 0 * P + 0 * (1-P) = 0
U2(H) = (-10) * P + 4 * (1-P)
U2(A) = U1(B)
∴ P = 2/7
即2混合策略纳什均衡（2/7，5/7）

【变式】加重逃税惩罚可以提高纳税意愿吗？（-10 -> -20）

U1(A) = 2 * Q + 4 * (1-Q)
U1(B) = 4 * Q + 0 * (1-Q)
U1(A) = U1(B)
∴ Q = 2/3
由于加重惩罚之前，Q = 2/3，
所以纳税人缴税意愿Q没变

• 影响纳税人交税意愿与惩罚力度无关
• 交税意愿与审计员策略概率相关（P）

U2(C) = 0 * P + 0 * (1-P) = 0
U2(H) = (-20) * P + 4 * (1-P)
U2(A) = U1(B)
∴ P = 1/6
P由2/7降到了1/6
意味着审查力度下降

• 提高惩罚逃税力度反而使得审查力度下降

• 提高纳税意愿 <— 提高审查率 <—

  • 提高成功逃税收益
  • 提高审查逃税收益
  • 降低审查成本

Famp.5 进化学模型

• 参与人：双参与人对称博弈

• 策略：基因表现

  • 合作C
  • 背叛D

• 收益：遗传适应性（适者生存）

• rule：

  • 种内斗争
  • 大量群体随机分配。D为突变（量少）
  • 不存在基因重组

• 说明：此模型讨论策略，没提参与人，Uc表示策略c的收益

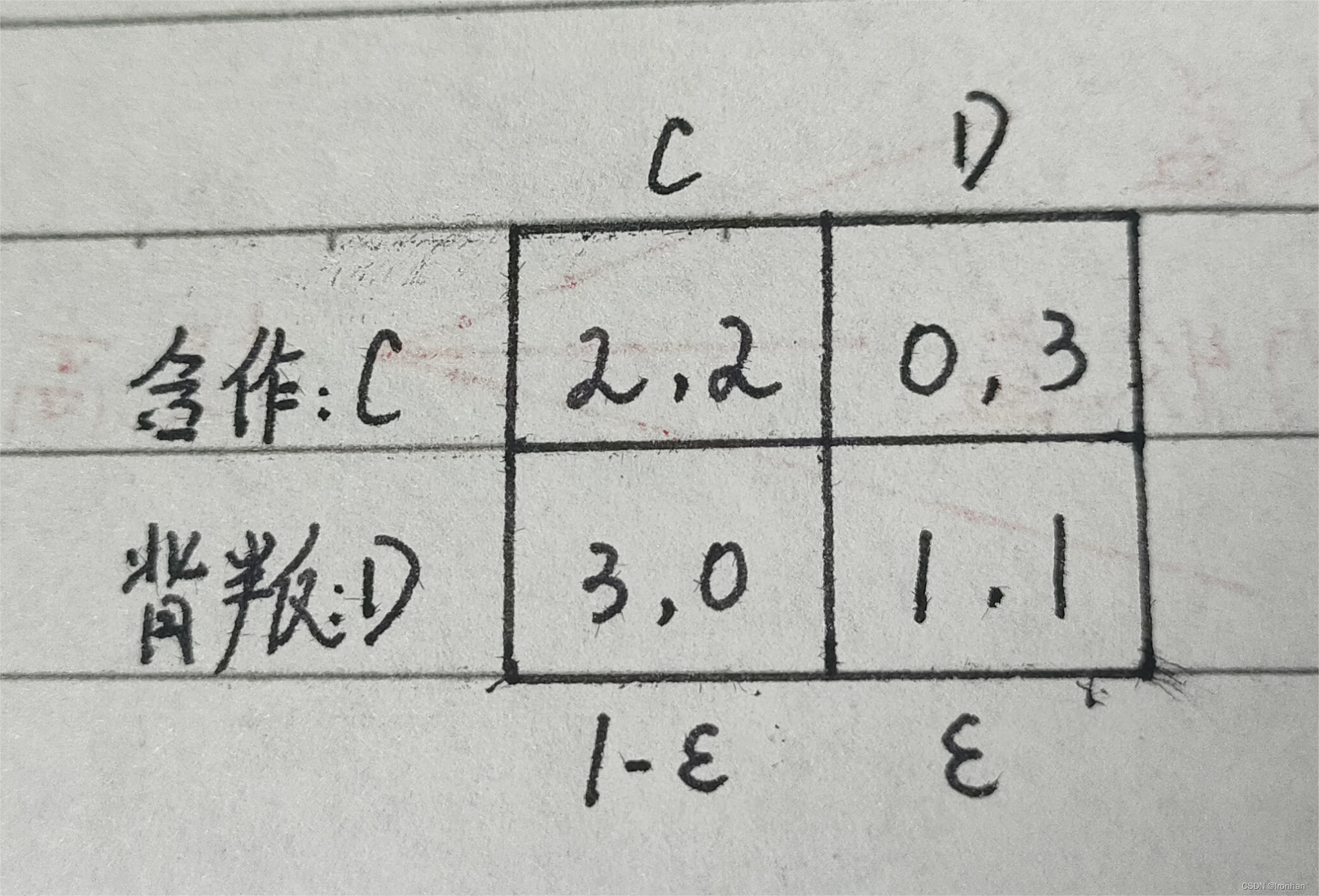
C(合作)具有进化稳定性(ES)吗？

UC = 2 * (1-ε) + 0 * ε
   = 2(1-ε)
UD = 3 * (1*ε) + 1 * ε
   = 3(1-ε) + ε
∴ UC < UD
∴ C不具有ES(进化稳定性)

• 自然选择进化的结果时很坏的
• 严格劣势策略不会是ES
• 本博弈中，D是ES

【变式】C是ES吗？

• C为本种群原策略，先考虑B，C

UC = 0 * (1-ε) + 1 * ε
   = ε
UB = 1 * (1-ε) + 0 * ε
   = 1 - ε
∴ UC < UB
∴ C不是ES		//此处推不出来B是ES

• 纳什均衡策略不一定是ES。

【思考】为什么纳什均衡策略不一定是ES

采取上图中的A，B部分
图中有两对纳什均衡，即(A,A)、(B,B)部分	//弱最佳
B是ES吗？
UB = 0
UA = 0 * (1-ε) + 1 * ε
   = ε
∴ UA > UB
∴ B不是ES
所以，纳什均衡策略不一定是ES

• 如果(s,s)是严格纳什均衡，那么s是ES

---

进化稳定性ES

Def. 生物学定义

• 在一个双参与人的对称博弈中，纯策略^s是ES，需要的条件：
  • 存在s’ > 0
  • (1 - ε)的概率下，^s对s和ε的概率下^s对s’的收益严格大于(1 - ε)的概率下，s’对^s和ε的概率下s’对s’的收益，对于任意s’都成立且对于任意s < s’都成立
  • (1 - ε) * U(^s,s) + ε * U(^s,s’) > (1 - ε) * U(s’,^s) + ε * U(s’,s’)

Def. 经济学定义

• 在一个双参与人的对称博弈中，纯策略^s是ES，需要的条件：
  • (^s,s)是对称纳什均衡，即：^s 对 ^s 的收益不小于任意 s’ 对 ^s 的收益
    • U(^s,s) >= U(s’,^s),对于任意s’恒成立
  • 当上一条件中，取等号时，即：U(^s,s) >= U(s’,^{s)时，必须U(}s,s’) > U(s’,s’)

Famp.

	A	B
A	1,1	1,1
B	1,1	0,0

• (A,A)是对称纳什均衡(非严格)
• 因为U(A,B) > U(B,B)，所以 A 是ES

Famp.

	L	R
L	2,2	0,0
R	0,0	1,1

• (L,L),(R,R)均为严格纳什均衡
• 即L，R均是ES
• 可以有多种ES的社会传统存在
• 这些策略不必一样好

---

鹰鸽之战

**Famp. **

【思考】1.D是ES吗？

即(D,D)是纳什均衡吗？
不是
∴ D不是ES

【思考】2.H是ES吗？

即(H,H)是纳什均衡吗？
①如果(V-C)/2 > 0;则H是纳什均衡(严格)，则H是ES
②如果(V-C)/2 = 0;则H是纳什均衡(非严格)，即U(H,H) = U(D,H)
	又∵U(H,D) = v > U(D,D) = V/2
	  ∴H是ES
③如果C > V,则H不是纳什均衡,则H不是ES

【思考】3.如果采取混合策略，其会是ES吗？

①找混合策略纳什均衡(P,1-P)
U(H,^P) = ((V-C)/2) * P + V * (1 - P)
U(D,^P) = 0 * P + (V/2) * (1 - p)
令U(H,^P) = U(D,^P)
∴ ^P = V/C
即混合策略纳什均衡(V/C,1 - V/C)
②判断：U(^P,P') > U(P',P') 对于任意P'成立
结果正确
∴混合策略(V/C,1 - V/C)是ES

• 混合策略不可能是严格纳什均衡
• 如果V < C,那么ES的种群中H派数量为V/C
  • V增大，H派增加
  • C增大，D派增加
• 收益：
  • D派：(1 - V/C)*(V/2) //混合策略(V/C,1 - V/C)利益相等，取一个即可
  • C增大时，UD增大
  • 原因：C增大时，会使得参与斗争着者减少；这样的减少使得D利益增大

---

Famp. 石头剪刀布

• 不存在纯策略纳什均衡
• 唯一可能ES：混合策略(1/3,1/3,1/3)

检验：证U(^P,P') > U(P',P')
设：P' = S
U(^P,S) = (1+V)/3
U(S,S) = 1
∵U(^P,S) < U(S,S)
∴混合策略(1/3,1/3,1/3)不是ES

• 本博弈无ES

---

行为有序博弈(贯序博弈)

Famp.

• 参与人2在做决定之前知道参与人1的策略，且参与人1知晓此情况

• 担保：降低不还款收益，这对自己产生了益处
• 逆向归纳法
  • 解决贯序博弈的主要方法

---

完全信息博弈

Def.

• 在任一节点上都知道自己处在整个博弈的哪个节点的博弈
• 使得逆向归纳法得以进行

---

纯策略

Def.

• 在一个完全信息博弈中，一号参与人的纯策略可以用树状图来表示，是一个完整的行动计划。

Famp.

---

信息集合

Def.

• 参与人②的信息集合时一系列参与人②无法识别的
• rule：以下两种不可计信息集合

---

完美信息

Def.

• 树状图上的所有信息集合包含每一个节点的博弈

---

纯策略·改

Def.

• 参与人i的纯策略是一个完全的行动计划，且它告诉i在他的每一个信息集合中如何做

Famp.

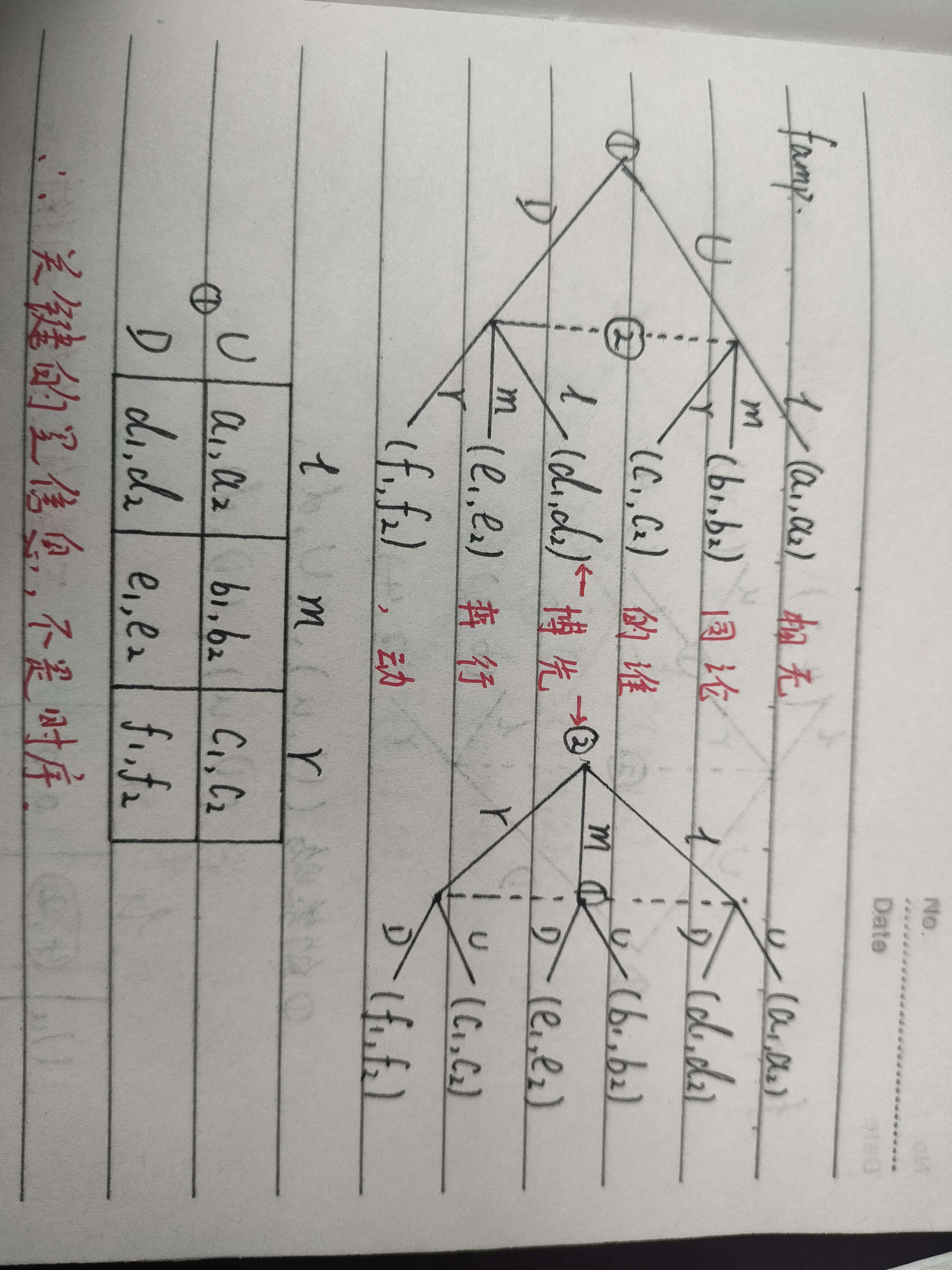
Famp.

Famp.

---

子博弈

Def.

• 博弈中的博弈
• 子博弈必须从单个节点开始(本身也是一个完整博弈)
• 它包含该节点的所有后续节点
• 他不能破坏任何信息集合

---

SPE子博弈完美均衡

Def.

• 如果策略(s1,s2,···,sn)能在一个子博弈中达到纳什均衡，那么它就是一个子博弈完美均衡。(其包含的每个子博弈必须满足纳什均衡)

---

重复博弈效果

Def.

• 在一个进行中的关系中，对于未来奖励的承担和未来惩罚的威胁，可能会为现在的好行为提供激励，但要有一个明确的"未来"
• 如果一个重复博弈的一个阶段博弈不止一个纳什均衡，我们可以通过预测不同策略的结果来为下一次行动提供激励。我们可以把这些激励当作现在合作行为的奖励或惩罚。

Famp. 竞争博弈(消耗战博弈<二轮>)

• 2 players
• 策略：
  • F //战斗
  • Q //退出
• 如果一方先退出，则另一方获胜(V)
• 如果双方都战斗，则双方均付出代价(-C),且博弈继续
• 如果双方都退出，则双方收益为0
• 设V>C

---

不对称信息

①信息可证实

Famp. 古诺博弈

• B成本：C^m //middle
• A成本：
  • C^h //high
  • C^m //middle
  • C^l //low
• A明确自己成本其它人不知道A成本

【思考】1. A是否应该公布自己的成本？(古诺竞争开始前)

• 这是一个信息披露过程，无论A是否公布，都是可以推测出来的
• “企业不想公布信息”——这本身也是在传达一种信息

②信息无法证实

• 一个好的信号要能通过成本不同的，即成本要有差别
• 计算方式：
  • (一天)背叛收益 - (一天)合作收益 < 持续收益
  • 应该选择合作

---

扣扳机策略

Def.

• 一开始选择合作，只要没人变卦，双方就会一直合作下去，一旦有人开始背叛，那么我们将永远选择背叛
• 通过扣扳机策略，可在囚徒困境中达到和解(先合作),这也是一个均衡策略
• 想让一段持续的关系能够促成今日的合作，如果这段关系有较大概率（大于1/3）持续下去，促成合作也是可以办到的（即对未来加权）

---

Famp.一回合内的惩罚措施策略

• 策略
  • 如果上回合是(c,c)或者(d,d)，选策略c //合作
  • 如果上回合是(c,d)或者(d,c)，选策略d //背叛
• 一回合内的惩罚措施是SPE
  • 需要对未来加权概率 > 1/2
• 平衡过程：
  • 如果你希望惩罚别太严，那么需要对未来的加权概率增大

Famp. 一次性投资

• 如果W = 1，则②会选择 骗
• 如果W >= 2，则②会选择 诚

【思考】改为多次投资，再次投资概率为α，则W为多少合适？（投资成本为2）

• 公式：今天欺骗收益 <= 持续合作收益 - 关系破裂威胁
  • 今天欺骗收益 = 2 - W
  • 持续合作收益 - 关系破裂威胁 = (W/(1 - α) - 1/(1 - ε))) * α
  • ε足够小
• 即：2（1 - α） + α <= W
  • 当α = 0时，W = 2。高于市场工资
  • 当α = 1时，W = 1。等于市场工资
  • 当α = 0.5时，W = 1.5。高于市场工资