SMO 算法流程
python代码见github
问题简介
SMO(Sequential Minimal Optimization)用于解决支持向量机中的对偶问题的最优化求解过程,该问题为:
m
a
x
α
∑
i
=
1
N
α
i
−
1
2
∑
i
=
1
N
∑
j
=
1
N
y
i
y
j
α
i
α
j
K
i
j
max_{\boldsymbol{\alpha}}\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}y_iy_j\alpha_i\alpha_jK_{ij}
maxαi=1∑Nαi−21i=1∑Nj=1∑NyiyjαiαjKij
s
.
t
.
0
≤
α
i
≤
C
,
∑
i
=
1
N
α
i
y
i
=
0
s.t.\ \ \ 0 \le \alpha_i \le C, \sum_{i=1}^N\alpha_iy_i=0
s.t. 0≤αi≤C,i=1∑Nαiyi=0
而此问题也满足KKT条件要求
{
α
i
≥
0
,
μ
i
≥
0
y
i
f
(
x
i
)
−
1
+
ξ
i
≤
0
α
i
(
y
i
f
(
x
i
)
−
1
+
ξ
i
)
=
0
ξ
i
≥
0
,
μ
i
ξ
i
=
0
\left\{ \begin{aligned} \alpha_i \ge 0, \mu_i \ge 0\\ y_if(\boldsymbol{x_i})-1+\xi_i \le 0\\ \alpha_i(y_if(\boldsymbol{x_i})-1+\xi_i) = 0 \\ \xi_i \ge 0, \mu_i\xi_i=0 \end{aligned} \right .
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧αi≥0,μi≥0yif(xi)−1+ξi≤0αi(yif(xi)−1+ξi)=0ξi≥0,μiξi=0
流程
该问题是一种凸二次规划问题,但是如果当作一般情况处理,计算过于繁琐。好在我们可以利用该问题特殊情况,得以特殊处理以简化流程。
SMO算法的核心思想是利用 ∑ i = 1 N α i y i = 0 \sum_{i=1}^N\alpha_iy_i=0 ∑i=1Nαiyi=0这一条件,进行特殊处理。由于一次性确定所有 α \alpha α的最优化取值是十分困难,所谓我们不妨每次只考虑变更两个变量 α i , α j \alpha_i,\alpha_j αi,αj,然后唯一确定剩下的变量为 ∑ k = 1 , k ≠ i , k ≠ j N α k y k = − ( α i y i + α j y j ) \sum_{k=1,k \ne i, k\ne j}^N\alpha_ky_k= - (\alpha_iy_i+\alpha_jy_j) ∑k=1,k=i,k=jNαkyk=−(αiyi+αjyj)。这里为什么选择两个变量,每次只选择一个不应该更容易吗?这里我们要注意,我们是通过迭代的方式每次选取一组 α \alpha α的值进行更改。鉴于条件 ∑ i = 1 N α i y i = 0 \sum_{i=1}^N\alpha_iy_i=0 ∑i=1Nαiyi=0,我们是无法对单一 α \alpha α进行修改的,换句话说,如果我们更改了一个变量 α i \alpha_i αi,则必须有另一个变量 α j \alpha_j αj跟随发生改变以满足 ∑ i = 1 N α i y i = 0 \sum_{i=1}^N\alpha_iy_i=0 ∑i=1Nαiyi=0。
以下,为了表述方便,我们每次选择的变量定为
α
1
,
α
2
\alpha_1,\alpha_2
α1,α2,此时目标函数可以写成:
W
(
α
1
,
α
2
)
=
α
1
+
α
2
−
1
2
K
11
y
1
2
α
1
2
−
1
2
K
22
y
2
2
α
2
2
−
K
12
y
1
y
2
α
1
α
2
−
y
1
α
1
∑
i
=
3
N
α
i
y
i
K
i
1
−
y
2
α
2
∑
i
=
3
N
α
i
y
i
K
i
2
+
C
W(\alpha_1,\alpha_2)=\alpha_1+\alpha_2-\frac{1}{2}K_{11}y_1^2\alpha_1^2-\frac{1}{2}K_{22}y_2^2\alpha_2^2 - K_{12}y_1y_2\alpha_1\alpha_2-y_1\alpha_1\sum_{i=3}^N\alpha_iy_iK_{i1}-y_2\alpha_2\sum_{i=3}^N\alpha_iy_iK_{i2}+C
W(α1,α2)=α1+α2−21K11y12α12−21K22y22α22−K12y1y2α1α2−y1α1i=3∑NαiyiKi1−y2α2i=3∑NαiyiKi2+C
这里我们把与
α
1
,
α
2
\alpha_1,\alpha_2
α1,α2无关的常数项都简写为
C
C
C,因为这部分在接下来的求导过程中无用。
这里引入我们之前的条件,并设定
α
1
y
1
+
α
2
y
2
=
−
∑
i
=
3
N
y
i
α
i
=
ζ
\alpha_1y_1+\alpha_2y_2=-\sum_{i=3}^Ny_i\alpha_i=\zeta
α1y1+α2y2=−i=3∑Nyiαi=ζ
α
1
=
(
ζ
−
α
2
y
2
)
y
1
\alpha_1=(\zeta -\alpha_2y_2)y_1
α1=(ζ−α2y2)y1
带入
W
W
W消去
α
1
\alpha_1
α1得
W
(
α
2
)
=
−
1
2
K
11
(
ζ
−
α
2
y
2
)
2
−
1
2
K
22
α
2
2
−
y
2
(
ζ
−
α
2
y
2
)
α
2
K
12
−
v
1
(
ζ
−
α
2
y
2
)
−
v
2
y
2
α
2
+
(
ζ
−
α
2
y
2
)
y
1
+
α
2
+
C
W(\alpha_2)=-\frac{1}{2}K_{11}(\zeta -\alpha_2y_2)^2-\frac{1}{2}K_{22}\alpha_2^2-y_2(\zeta-\alpha_2y_2)\alpha_2K_{12}-v_1(\zeta-\alpha_2y_2)-v_2y_2\alpha_2+(\zeta -\alpha_2y_2)y_1+\alpha_2+C
W(α2)=−21K11(ζ−α2y2)2−21K22α22−y2(ζ−α2y2)α2K12−v1(ζ−α2y2)−v2y2α2+(ζ−α2y2)y1+α2+C
其中
v
1
=
∑
i
=
3
N
α
i
y
i
K
i
1
v_1=\sum_{i=3}^N \alpha_iy_iK_{i1}
v1=i=3∑NαiyiKi1
v
2
=
∑
i
=
3
N
α
i
y
i
K
1
j
v_2=\sum_{i=3}^N \alpha_iy_iK_{1j}
v2=i=3∑NαiyiK1j
我们需要对其最大化,这里进行求导,赋值0求极值
W ′ ( α 2 ) = − ( K 11 + K 22 − 2 K 12 ) α 2 + K 11 ζ y 2 − K 12 ζ y 2 + v 1 y 2 − v 2 y 2 − y 1 y 2 + y 2 2 = 0 W'(\alpha_2)=-(K_{11}+K_{22}-2K_{12})\alpha_2+K_{11}\zeta y_2-K_{12}\zeta y_2 + v_1y_2-v_2y_2-y_1y_2+y_2^2=0 W′(α2)=−(K11+K22−2K12)α2+K11ζy2−K12ζy2+v1y2−v2y2−y1y2+y22=0
至此,问题似乎得以解决,我们似乎只需要通过该等式解出 α 2 \alpha_2 α2即可。但是,请再次注意,我们是通过迭代的方式每次选取一组 α \alpha α进行优化的。而注意到变量 ζ \zeta ζ,它的取值为: − ∑ i = 3 N y i α i -\sum_{i=3}^Ny_i\alpha_i −∑i=3Nyiαi,其中其他的 α \alpha α变量我们无法获悉。我们只知道在之前的迭代中确定的旧值。
所以,这里我们考虑如何调整 α 1 , α 2 \alpha_1,\alpha_2 α1,α2的数值。即,如何通过旧值推定出新值。我们假定,在之前的迭代中已经确定了一个拟定分隔超平面
f ( x ) = w T x + b = ∑ i = 1 N α i ∗ y i K x i T x + b f(x)=\boldsymbol{w^Tx}+b=\sum_{i=1}^N \alpha^*_iy_iK_{\boldsymbol{x_i^Tx}}+b f(x)=wTx+b=i=1∑Nαi∗yiKxiTx+b
这里
α
∗
\alpha^*
α∗为上一次迭代中的旧的值。这里我们明确,在此轮迭代中,改变的只有
α
1
,
α
2
\alpha_1,\alpha_2
α1,α2,所以有
∑
i
=
3
N
α
i
y
i
K
i
1
=
∑
i
=
3
N
α
i
∗
y
i
K
i
1
\sum_{i=3}^N \alpha_iy_iK_{i1}=\sum_{i=3}^N \alpha^*_iy_iK_{i1}
i=3∑NαiyiKi1=i=3∑Nαi∗yiKi1
∑
i
=
3
N
α
i
y
i
K
1
i
=
∑
i
=
3
N
α
i
∗
y
i
K
1
i
\sum_{i=3}^N \alpha_iy_iK_{1i}=\sum_{i=3}^N \alpha^*_iy_iK_{1i}
i=3∑NαiyiK1i=i=3∑Nαi∗yiK1i
所以我们将 f f f带入 v 1 , v 2 v_1,v_2 v1,v2
v
1
=
f
(
x
1
)
−
α
1
∗
y
1
K
11
−
α
2
∗
y
2
K
12
−
b
v_1=f(x_1)-\alpha^*_1y_1K_{11}-\alpha^*_2y_2K_{12}-b
v1=f(x1)−α1∗y1K11−α2∗y2K12−b
v
2
=
f
(
x
2
)
−
α
1
∗
y
1
K
12
−
α
2
∗
y
2
K
22
−
b
v_2=f(x_2)-\alpha^*_1y_1K_{12}-\alpha^*_2y_2K_{22}-b
v2=f(x2)−α1∗y1K12−α2∗y2K22−b
将其带入 W ( α 2 ) = 0 W(\alpha_2)=0 W(α2)=0得
α
2
=
α
2
∗
+
y
2
(
E
1
−
E
2
)
η
\alpha_2=\alpha_2^*+\frac{y_2(E_1-E_2)}{\eta}
α2=α2∗+ηy2(E1−E2)
η
=
K
11
+
K
22
−
2
K
12
\eta = K_{11}+K_{22}-2K_{12}
η=K11+K22−2K12
其中 E E E为误差函数
E i = f ( x i ) − y i E_i=f(x_i)-y_i Ei=f(xi)−yi
但此时,我们还没有考虑到条件:
s
.
t
.
0
≤
α
i
≤
C
,
s.t.\ \ \ 0 \le \alpha_i \le C,
s.t. 0≤αi≤C,
α
1
y
1
+
α
2
y
2
=
−
∑
i
=
3
N
y
i
α
i
=
ζ
\alpha_1y_1+\alpha_2y_2=-\sum_{i=3}^Ny_i\alpha_i=\zeta
α1y1+α2y2=−i=3∑Nyiαi=ζ
由于 y ∈ { − 1 , + 1 } y\in \{-1,+1\} y∈{−1,+1},故,上式无非就四种情况
α
1
+
α
2
=
ζ
(1)
\alpha_1+\alpha_2=\zeta\tag 1
α1+α2=ζ(1)
α
1
−
α
2
=
ζ
(2)
\alpha_1-\alpha_2=\zeta\tag 2
α1−α2=ζ(2)
−
α
1
+
α
2
=
ζ
(3)
-\alpha_1+\alpha_2=\zeta\tag 3
−α1+α2=ζ(3)
α
1
+
α
2
=
−
ζ
(4)
\alpha_1+\alpha_2=-\zeta\tag 4
α1+α2=−ζ(4)
其中(2)(3)可以归为一种情况
α
1
−
α
2
=
k
\alpha_1-\alpha_2=k
α1−α2=k 其中
k
k
k可以归结为
ζ
,
−
ζ
\zeta,-\zeta
ζ,−ζ。
满足线性规划
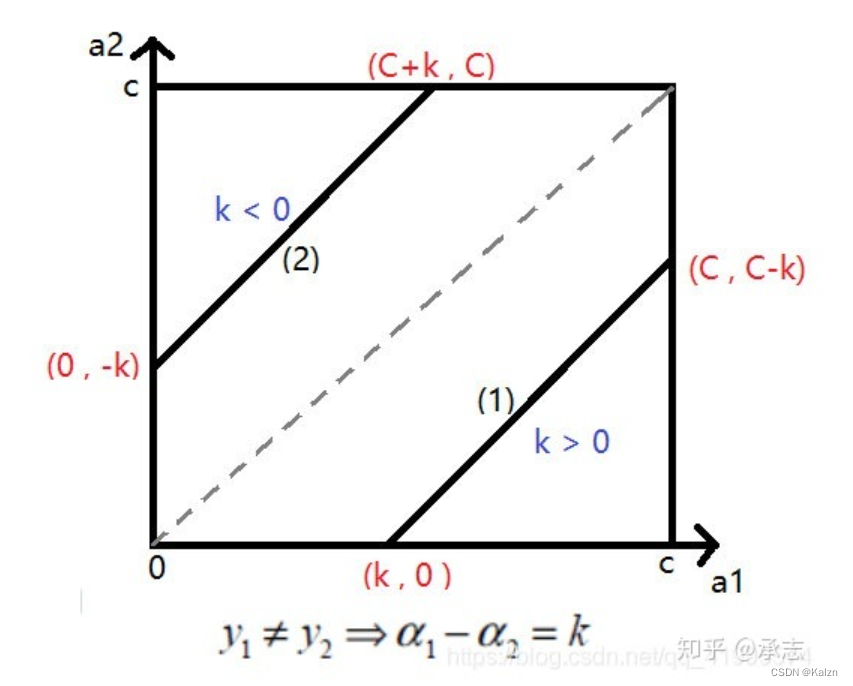
在这种情况下,应满足
α
2
∈
[
m
a
x
(
0
,
−
k
)
,
m
i
n
(
C
,
C
+
k
)
]
\alpha_2 \in [max(0, -k), min(C, C+k)]
α2∈[max(0,−k),min(C,C+k)]
。定义
L
=
m
a
x
(
0
,
−
k
)
,
H
=
m
i
n
(
C
,
C
+
k
)
L=max(0,-k),H=min(C,C+k)
L=max(0,−k),H=min(C,C+k)
此外,(1)(4)可以归为另一种情况
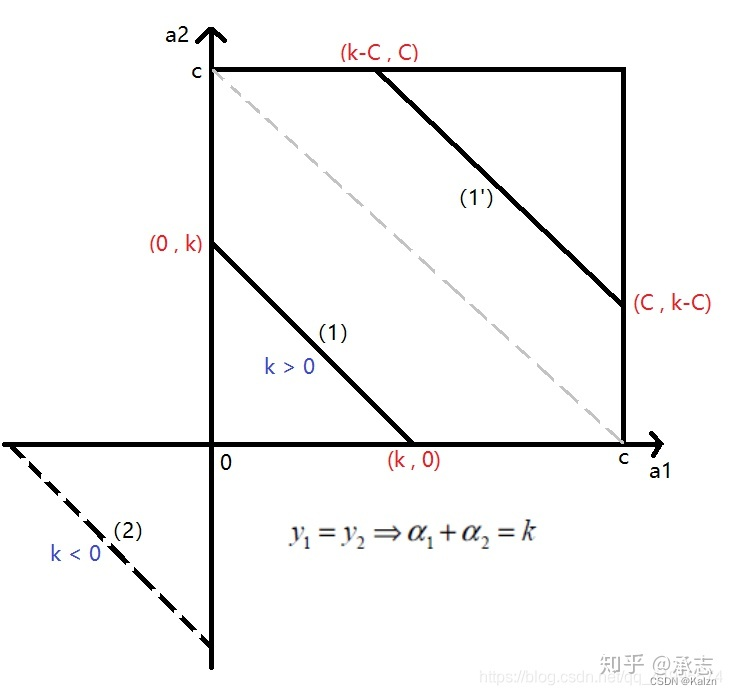
在这种情况下,应满足 α 2 ∈ [ m a x ( 0 , k − C ) , m i n ( C , k ) ] \alpha_2 \in [max(0, k-C), min(C, k)] α2∈[max(0,k−C),min(C,k)]。定义 L = m a x ( 0 , k − C ) , H = m i n ( C , k ) L=max(0,k-C),H=min(C,k) L=max(0,k−C),H=min(C,k)
所以最后更新 α 2 \alpha_2 α2
α
2
=
{
L
α
2
≤
L
M
L
≤
α
2
≤
H
H
α
2
≥
H
\alpha_2=\left \{ \begin{aligned} L & \ \ \ \ \alpha_2 \le L \\ M & \ \ \ \ L \le \alpha_2 \le H\\ H & \ \ \ \ \alpha_2 \ge H \\ \end{aligned} \right .
α2=⎩⎪⎨⎪⎧LMH α2≤L L≤α2≤H α2≥H
M
=
α
2
∗
+
y
2
(
E
1
−
E
2
)
η
M=\alpha_2^*+\frac{y_2(E_1-E_2)}{\eta}
M=α2∗+ηy2(E1−E2)
至此我们确定了
α
2
\alpha_2
α2得更新值,然后
α
1
\alpha_1
α1的值也随之推出。这里我们设
Δ
α
2
=
(
α
2
−
α
2
∗
)
\Delta\alpha_2=(\alpha_2 - \alpha_2^*)
Δα2=(α2−α2∗)
则有
α
1
=
α
1
∗
−
y
1
y
2
Δ
α
2
\alpha_1 = \alpha_1^*-y_1y_2\Delta\alpha_2
α1=α1∗−y1y2Δα2
这里我们需要明确一件事情,到目前为止,我们所作的事情就是求 W ( α 2 ) W(\alpha_2) W(α2)这个目标函数得极值,通过分析可以发现 W ( α 2 ) W(\alpha_2) W(α2)是一个二次多项式函数,而二次项的系数为 η \eta η。所以目前来说,上述结论仅在 η > 0 \eta>0 η>0时成立,因为此时 W ( α 2 ) W(\alpha_2) W(α2)是个开口向下的二次函数,存在极值为最小值。这种情况实际上可以应对大部分情况。但是在一部分情况 η ≤ 0 \eta \le 0 η≤0,此时函数极小值在定义域边界出现。当然,在算法的实际实现中,我们可以直接求出定义域的两端值和极值,然后取三者中的最小值即可。
接下来,我们将讨论偏置 b b b的值如何求出。根据KKT条件 y 1 ( w T x 1 + b ) = 1 , y 1 ∈ − 1 , + 1 y_1(\boldsymbol{w^Tx_1}+b)=1,y_1\in{-1,+1} y1(wTx1+b)=1,y1∈−1,+1可得 ∑ i = 1 N α i y i K i 1 = y 1 \sum_{i=1}^N\alpha_iy_iK_{i1}=y_1 ∑i=1NαiyiKi1=y1,即有
b
1
=
y
1
−
∑
i
=
3
N
α
i
∗
y
i
K
i
1
−
α
1
y
1
K
11
−
α
2
y
2
K
21
b_1=y_1-\sum_{i=3}^N\alpha_i^*y_iK_{i1}-\alpha_1y_1K_{11}-\alpha_2y_2K_{21}
b1=y1−i=3∑Nαi∗yiKi1−α1y1K11−α2y2K21
带入误差函数
E
E
E得
y
1
−
∑
i
=
3
N
α
i
∗
y
i
K
i
1
=
−
E
1
+
α
1
∗
y
1
K
11
+
α
2
∗
y
2
K
11
+
b
∗
y_1-\sum_{i=3}^N\alpha_i^*y_iK_{i1}=-E_1+\alpha_1^*y_1K_{11}+\alpha_2^*y_2K_{11}+b^*
y1−i=3∑Nαi∗yiKi1=−E1+α1∗y1K11+α2∗y2K11+b∗
其中
b
∗
b^*
b∗为旧的偏置值,将该式子代入替换上式的前两项
b
1
=
−
E
1
−
y
1
K
11
(
α
1
−
α
1
∗
)
−
y
2
K
21
(
α
2
−
α
2
∗
)
+
b
∗
b_1=-E_1-y_1K_{11}(\alpha_1-\alpha_1^*)-y_2K_{21}(\alpha_2-\alpha_2^*)+b^*
b1=−E1−y1K11(α1−α1∗)−y2K21(α2−α2∗)+b∗
同理可以得出
b
2
=
−
E
2
−
y
1
K
12
(
α
1
−
α
1
∗
)
−
y
2
K
22
(
α
2
−
α
2
∗
)
+
b
∗
b_2=-E_2-y_1K_{12}(\alpha_1-\alpha_1^*)-y_2K_{22}(\alpha_2-\alpha_2^*)+b^*
b2=−E2−y1K12(α1−α1∗)−y2K22(α2−α2∗)+b∗
而最终的
b
b
b要取两者的中间值,即
b
=
b
1
+
b
2
2
b=\frac{b_1+b_2}{2}
b=2b1+b2
最后,我们来讨论,如何进行变量的选取。首先我们应该确定第一个变量,此时,我们变量样本集,选取第一个不满足KKT条件的样本。这里写作KKT条件为:
α
i
=
0
⟹
y
(
i
)
(
w
T
x
(
i
)
+
b
)
≥
1
\alpha_i=0 \Longrightarrow y^{(i)}(w^Tx^{(i)}+b) \ge 1
αi=0⟹y(i)(wTx(i)+b)≥1
α
i
=
C
⟹
y
(
i
)
(
w
T
x
(
i
)
+
b
)
≤
1
\alpha_i=C \Longrightarrow y^{(i)}(w^Tx^{(i)}+b) \le 1
αi=C⟹y(i)(wTx(i)+b)≤1
0
≤
α
i
≤
C
⟹
y
(
i
)
(
w
T
x
(
i
)
+
b
)
=
1
0 \le \alpha_i \le C \Longrightarrow y^{(i)}(w^Tx^{(i)}+b) = 1
0≤αi≤C⟹y(i)(wTx(i)+b)=1
然后依照规则选取第二个变量,执行优化。当完成后,我们开始遍历非边界样例集(即满足 0 < α i < C 0<\alpha_i<C 0<αi<C的样例),同样选择第一个不满足KKT条件的变量,然后依照一定规则选择出第二个变量进行优化。完成后,我们再次选择整个样本集进行以上操作。总得来说,我们交替选择整个样本集和非边界样本集进行优化,直至整个样本集全部满足KKT条件。
关于选取第二个变量的规则,我们的原则是让
α
2
\alpha_2
α2尽可能大的发生变化,由于
α
1
\alpha_1
α1依赖
∣
E
1
−
E
2
∣
|E_1-E_2|
∣E1−E2∣所以当
E
1
E_1
E1为正,则
E
2
E_2
E2要尽量小,否则
E
2
E_2
E2要尽量大。
有时按照上述的启发式选择第二个变量,不能够使得函数值有足够的下降,这时按下述步骤:
首先在非边界集上选择能够使函数值足够下降的样本作为第二个变量,
如果非边界集上没有,则在整个样本集上选择第二个变量,
如果整个样本集依然不存在,则重新选择第一个变量。
参考
1.https://blog.csdn.net/luoshixian099/article/details/51227754
2.https://www.cnblogs.com/jerrylead/archive/2011/03/18/1988419.html
3.https://www.jianshu.com/p/0c433f6f4141
4.https://zhuanlan.zhihu.com/p/257866920
5.John Platt.Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines (https://www.microsoft.com/en-us/research/publication/sequential-minimal-optimization-a-fast-algorithm-for-training-support-vector-machines/)





















 520
520

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








