伯努利数与自然数幂和

自然数幂和的伯努利数做法是对于指数型母函数的精彩应用。
普通的母函数是因为对于等比数列的研究可以迁移到幂级数上，从而拓展生成函数的运算而简化运算，一般化数列的运算。
指数型母函数是将泰勒展开的研究迁移到幂/阶乘级数（？？？）而规定生成函数的运算，从而达到描述数列运算的目的。

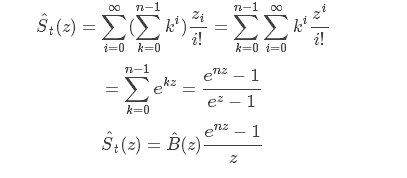
这个证明很简洁。
$B(z)=\frac{z}{e^z-1}$
也就是$B(z)\frac{e^z-1}{z}=1$
${\sum }_{i=0}^n\frac{B_i}{i!}\times \frac{1}{(n-i+1)!}=[n=1]$
两边同时$\times n!$就是
${\sum }_{i=0}^n{B}_i\left(\genfrac{}{}{0ex}{}{n+1}{i}\right)=[n=1]$
然后 答案就是 $B(z)$ 与 $\frac{e^{nz}-1}{z}$的卷积的第$k+1$项。
记住$B(z)=\frac{\sum B_i{x}^i}{i!}$
$\frac{e^{nz}-1}{z}=\frac{\sum n^i{x}^{i-1}}{i!}$
可以推出
$\frac{S_k}{k!}={\sum }_{i=0}^k\frac{Bi}{i!}\ast \frac{n^{k+1-i}}{(k+1-i)!}$
即$S_k=\frac{1}{k+1}{\sum }_{i=0}^k\left(\genfrac{}{}{0ex}{}{k+1}{i}\right)B_i{n}^{k+1-i}$
这就是网上的神奇公式。
这里要注意一下，伯努利数不一定是整数，所以这个式子不可以拿来证明1~n的自然数幂和被n整除。
这个式子的好处在于，你只需要计算一次伯努利数，之后都可以用，但是对于模数的要求。。。。
请用第二类斯特林数。

为什么伯努利数分子上有一个$z$?
因为不这样的话就有一项$z^{-1}$
对于伯努利数更自然的描述式应该是这个：
$B_n={\sum }_{i=0}^n{B}_i\left(\genfrac{}{}{0ex}{}{n}{i}\right),n>1$
可以等价于指数生成函数的：
$B(x)+x=B(x)e^x$
左边由于$n>1$的限制需要$+x$
那么可以得到$B(x)=\frac{x}{e^x-1}$

但是递推的时候因为$B_n$会被消掉，用这个式子算$B_{n-1}$。。。。
记得$B_0=1$

关于$B^{+}$和$B^{-}$

51nod 1228 O(k^2)伯努利数模板。

#include<bits/stdc++.h>
#define mod 1000000007
#define maxn 2005
#define LL long long
using namespace std;

int B[maxn],C[maxn][maxn],inv[maxn];

int main()
{
	inv[0] = inv[1] = 1;
	for(int i=0;i<maxn;i++)
	{
		if(i > 1) inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
		C[i][0] = 1;
		for(int j=1;j<=i;j++) 
			C[i][j] = (C[i-1][j-1] + C[i-1][j]) % mod;
	}
	
	B[0] = 1; 
	for(int i=1;i<maxn-1;i++)
	{
		for(int j=0;j<i;j++) B[i] = (B[i] - 1ll * B[j] * C[i+1][j]) % mod;
		B[i] = 1ll * B[i] * inv[i+1] % mod;
	}
	
	int T;
	for(scanf("%d",&T);T--;)
	{
		LL n , k;
		scanf("%lld%lld",&n,&k);
		n %= mod;
		int ans = 0;
		for(int i=1,pw=n+1;i<=k+1;i++,pw=(1ll * pw * n + pw) % mod)
			ans = (ans + 1ll * C[k+1][i] * B[k+1-i] % mod * pw) % mod;
		printf("%lld\n",((1ll * ans * inv[k+1]) % mod + mod) % mod);
	}
}

51 nod 1258 V4
多项式求逆$nlogn$

#include<bits/stdc++.h>
#define maxn 200005
#define M ((1<<15)-1)
#define mod 1000000007
#define LL long long
using namespace std;

const double Pi = 3.1415926535897932384626433832795;
struct cplx
{
	double r,i;
	cplx(double r=0,double i=0):r(r),i(i){}
	cplx operator +(const cplx &B)const{ return cplx(r+B.r,i+B.i); }
	cplx operator -(const cplx &B)const{ return cplx(r-B.r,i-B.i); }
	cplx operator *(const cplx &B)const{ return cplx(r*B.r-i*B.i,r*B.i+i*B.r); }
	cplx conj(){ return cplx(r,-i); }
}w[maxn];
int r[maxn],wlen;

inline void FFT(cplx A[maxn],int lgn,int tp)
{
	int n = 1<<lgn;
	for(int i=1;i<n;i++) r[i] = (r[i>>1]>>1)|((i&1)<<(lgn-1));
	for(int i=1;i<n;i++) if(i<r[i]) swap(A[i],A[r[i]]);
	for(int L=2;L<=n;L<<=1)
		for(int st=0,l=L>>1,inc=wlen/l;st<n;st+=L)
			for(int k=0,loc=0;k<l;k++,loc+=inc)
			{
				cplx tmp = (tp==1?w[loc]:w[loc].conj())*A[st+k+l];
				A[st+k+l]=A[st+k]-tmp,A[st+k]=A[st+k]+tmp;
			}
	if(tp==-1) for(int i=0;i<n;i++) A[i].r/=n,A[i].i/=n;
}

cplx s[4][maxn];
inline void mul(int a[maxn],int b[maxn],int lgn,int c[maxn])
{
	if(lgn == 14)
		lgn = 14;
	int n = 1<<lgn;
	for(int i=0;i<n;i++) s[0][i]=cplx(a[i]>>15,b[i]>>15),s[1][i]=cplx(a[i]&M,b[i]&M);
	FFT(s[0],lgn,1),FFT(s[1],lgn,1);
	for(int i=0;i<n;i++)
	{	cplx a[4]={s[0][i],s[0][(n-i)&(n-1)].conj(),s[1][i],s[1][(n-i)&(n-1)].conj()};
		cplx b[4]={(a[0]+a[1])*cplx(0.5,0),(a[0]-a[1])*cplx(0,-0.5),(a[2]+a[3])*cplx(0.5,0),(a[2]-a[3])*cplx(0,-0.5)};
		s[2][i]=b[0]*b[1]+cplx(0,1)*b[2]*b[3],s[3][i]=b[0]*b[3]+cplx(0,1)*b[1]*b[2]; }
	FFT(s[2],lgn,-1),FFT(s[3],lgn,-1);
	for(int i=0;i<n;i++) 
	{ 	LL a[4]={llround(s[2][i].r)%mod,llround(s[2][i].i)%mod,llround(s[3][i].r)%mod,llround(s[3][i].i)%mod}; 
		c[i]=((a[0]<<30)+a[1]+((a[2]+a[3])<<15))%mod; }
}

int Pow(int base,int k)
{ int ret=1;for(;k;k>>=1,base=1ll*base*base%mod) if(k&1)ret=1ll*ret*base%mod; return ret; }
void Inv(int a[maxn],int lgn,int b[maxn])
{	if(lgn==0){ b[0]=Pow(a[0],mod-2);return; }
	Inv(a,lgn-1,b);
	int n = 1<<(lgn+1);
	static int tmp[3][maxn];
	for(int i=0;i<n;i++)
	{	if(i<(n>>1)) tmp[0][i] = a[i]; else tmp[0][i] = 0;
		if(i<(n>>2)) tmp[1][i] = b[i]; else tmp[1][i] = 0; }
	mul(tmp[0],tmp[1],lgn+1,tmp[2]);
	for(int i=0;i<n;i++) tmp[2][i] = (i==0) * 2 - tmp[2][i];
	mul(tmp[2],tmp[1],lgn+1,b);
	for(int i=(n>>1);i<n;i++) b[i]=0;
}

int a[maxn],B[maxn],inv[maxn]={1,1},invf[maxn]={1,1};
int main()
{
	int lgn = 16; wlen = 1<<16;
	for(int i=0;i<65536;i++) 
	{
		if(i>1)inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod,
			invf[i] = 1ll  * invf[i-1] * inv[i] % mod;
		w[i] = cplx(cos(i*Pi/wlen),sin(i*Pi/wlen));
	}
	for(int i=0;i<65536;i++) a[i] = invf[i+1];
	Inv(a,lgn,B);
	for(int i=0,fac=1;i<65536;i++,fac=1ll*fac*i%mod)
		B[i] = (1ll * B[i] * fac % mod + mod)%mod;
	
	int T;
	for(scanf("%d",&T);T--;)
	{
		LL n , k;
		scanf("%lld%lld",&n,&k);
		n %= mod;
		int ans = 0;
		for(int i=1,pw=(n+1),C=k+1;i<=k+1;i++,pw=(1ll*pw*n+pw)%mod,C=1ll*C*inv[i]%mod*(k+2-i)%mod)
			ans = (ans + 1ll * C * B[k+1-i] % mod * pw) % mod;
		printf("%d\n",(1ll*ans*inv[k+1]%mod+mod)%mod);
	}
}