Engle 在文章首次提出可以运用DCC-GARCH 模型(DynamicConditional Corelational Autoregressive Conditional Heteroscedasticity Model),即动态相关多变量广义自回归条件异方差模型来度量两个或者多个不同时间序列数据的动态波动相关性。该模型放宽了CCC-GARCH模型中对时间序列数据相关性的波动系数为常数的假设条件,认为实际情况下时间序列数据波动是时变的。在这篇论文发表后,国内外很多专家学者不断对其进行理论丰富和实证扩充,逐渐建立起关于DCC-GARCH模型成熟完善的理论体系。
下面用r来实现dcc garch模型
效果如下:

时变相关系数图
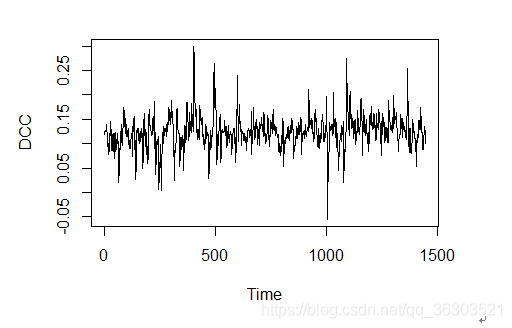
R代码如下:
library(ccgarch);
library(fGarch);
library(MASS);
library(FinTS);
library(tseries);
library(vars);
x=read.csv("C:\\wx公众号\\统计分析分析\\qq.csv");
xt<-ts(x[,1:2],start=c(1,1));
plot(xt, plot.type = "single",col=c("red","black"),lty=1:2);
leg.names<-c("上证指数收益","道琼斯指数收益");
legend(locator(1),leg.names,lty=c(1,2), col=c("red","black"));
y=xt[,1];
z=xt[,2]







 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 3025
3025











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








