R语言DCC-GARCH模型

最新推荐文章于 2024-08-08 18:53:59 发布

月旧儿

最新推荐文章于 2024-08-08 18:53:59 发布

阅读量2.7w

点赞数 37

文章标签： r语言

本文链接：https://blog.csdn.net/weixin_44653805/article/details/105652030

版权

本文介绍了使用R语言建立DCC-GARCH模型的步骤，包括时间序列的对数化和差分、单位根检验、ARMA模型构建、残差自相关性检验、GARCH模型拟合及DCC-GARCH模型的应用，强调了在每个步骤中的关键检验和图形分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

感谢nie chun xiao
首先简述一下对一个时间序列建立DCC-GARCH模型的步骤：
1.通常时间序列不平稳，且经常对时间序列取对数化。所以第一步先取对数化、差分（是为了解决序列不平稳的问题）。
2.adf单位根检验显示平稳后，建立ARMA模型，用来提取方差。
3.用LB检验残差项是否存在自相关性，防止对下一步残差平方的自相关检验产生影响。
4.当残差项不存在自相关性，进一步用LB检验残差项的平方是否存在自相关性。当检验p值很小拒绝原假设，表明存在自相关性，满足建立GARCH模型的前提条件。
5. 检验ARMA模型残差是否存在ARCH效应,若存在，可以建立GARCH模型
6. 对收益率序列拟合GARCH模型
7. 对收益率序列进行DCC-GARCH模型的拟合，选择0-4绘制相关图示。

本人的数据形式如下。从Excel中复制粘贴到了txt中。

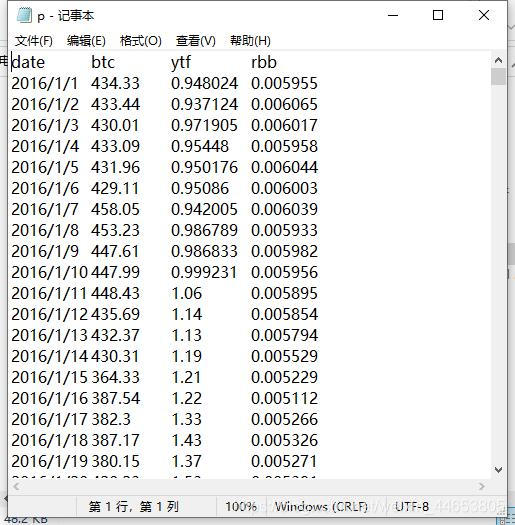
在这里插入图片描述

导入数据，并绘制三个样本序列的价格序列图。

p=read.table('C:/Users/dqxq767/Documents/R/p.txt',sep = '\t',header = T)
time=as.Date(p$'date',"%Y/%m/%d")
p1=ts(p[,2:4])
install.packages('zoo')
library(zoo)
par(mfrow=c(1,1),oma=c(0.2,0.2,0.2,0.2)) 
plot(zoo(p1,time),xlab="time",ylab="价格美元", plot.type = "single",col=c("red","black","yellow","green"),lty=1:3,main="样本的价格序列");
par(mfrow=c(1,3),oma=c(0.2,0.2,0.2,0.2))  
plot(zoo(p1[,1],time),xlab="time",ylab="价格美元",main="比特币价格序列")
plot(zoo(xt[,2],time),xlab="time",ylab="价格美元",main="以太坊价格序列")
plot(zoo(xt[,3],time),xlab="time",ylab="价格美元",main="瑞波币价格序列")

计算相关系数矩阵

p1cor=cor(p1)             ##相关系数矩阵
p1cor

计算基本统计量最大值、最小值、中位数、偏度、峰度、极值

install.packages('DistributionUtils')
library(DistributionUtils)      #基本统计量计算
data_outline = function(x){
   
  m = mean(x)
  d=max(x)
  xd=min(x)
  me = median(x)
  s = sd(x)
  kur=kurtosis(x)
  ske=skewness(x)
  R = max(x)-min(x)
  data.frame( Mean=m,  Median=me, max=d,min=xd,std_dev=s,
             Skewness=ske, Kurtosis=kur, R=R)
}
for (i in  1:3){