第六章_定积分的应用

6.1 几何应用

6.1.1	平面图形的面积
6.1.2	旋转体体积
6.1.3	曲线弧长
6.1.4	旋转体侧面积

从二重积分的角度复习平面图形的面积以及旋转体的体积

6.1.1 平面图形的面积

平面图形的面积根据直角坐标系与极坐标系有两种不同的方法，需要掌握两种公式；
其实换一种思路，其面积实质上是在该区域对1作二重积分，故而不需要再记忆公式。
上图中，
直角坐标系下，先对x后对y
极坐标系下，先对cita，后对rou

6.1.2 旋转体的体积

上述公式为传统方法，只适用于围绕坐标轴旋转的情形，当旋转轴围绕非坐标轴时，只能由元素法思想自己推导，虽不失为一种方法，但对于考研来说，并不是最佳（效率最高）方法。

旋转体体积一般问题
同面积一样，用二重积分的思想做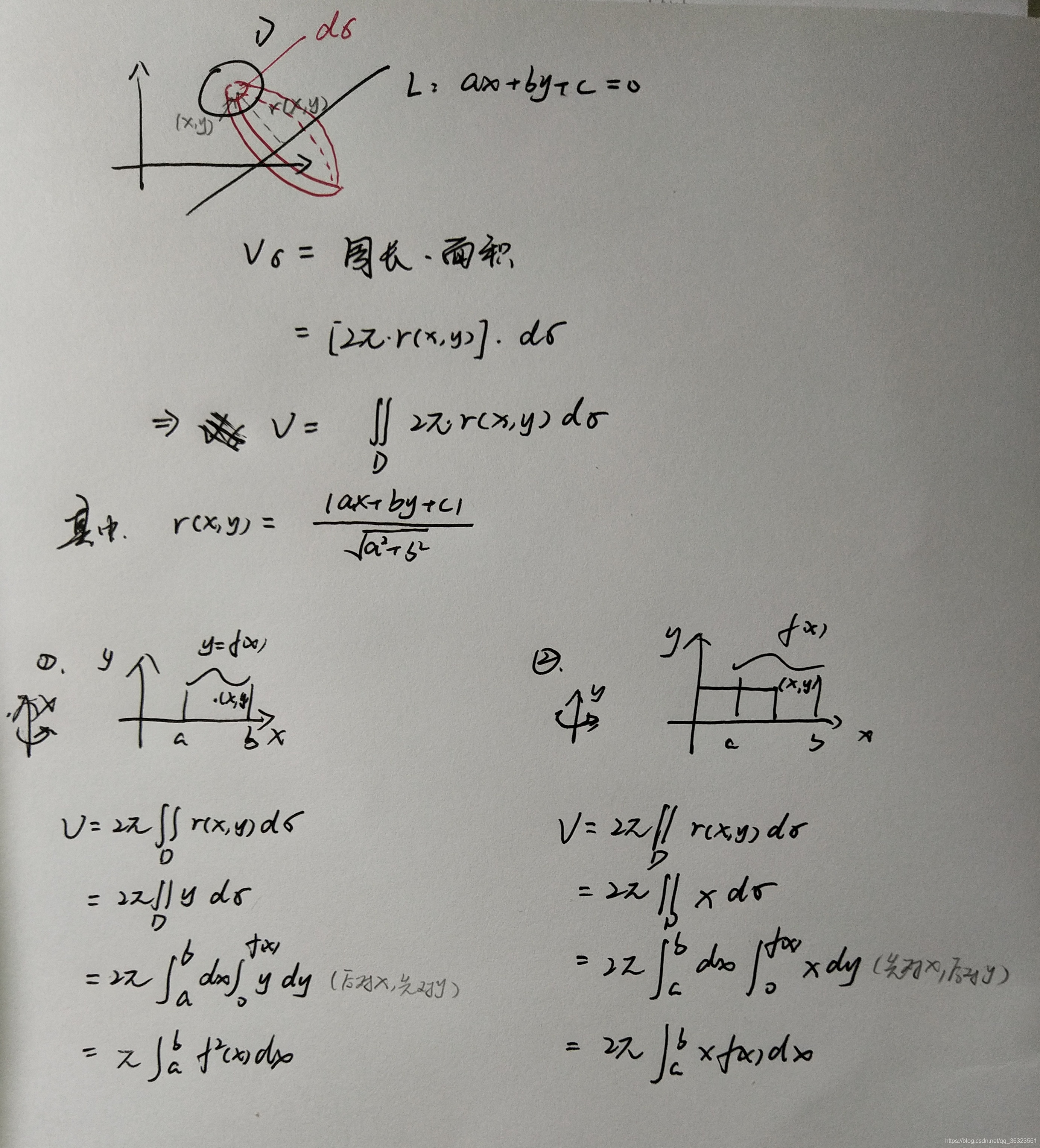

从二重积分的角度复习旋转体体积

6.1.3 曲线弧长

在三种不同形式下的方程，求弧微分的形式不同

6.1.4 旋转体侧面积

关于侧面积使用dx和ds的选择，
牵扯到微元法和元素法的基本原理，先找这个区间上对应量的近似值，然后找微元，然后再积分，但这个近似值有精度要求，即找到的近似值忽略掉的是x的高阶无穷小，若是用dx，则丢掉的就不是高阶无穷小了，所以必须用ds

总结：这里有四个问题，面积，体积，弧长，侧面积；
对于后面两种（弧长和侧面积，都必须用ds），而面积和体积可以用dx

6.2 物理应用

一般就三种问题：压力、变力做功、引力

6.3 常考题型与典型例题

（一）平面域面积和旋转体体积的计算

【真】