T:
n项和极限的求法
目前为止(至定积分),仅有两种算法
① 夹逼定理
② 定积分定理
关于两种方法的选择:
一般考虑这两类方法的题目都是带有分母的题,可将分母分成主体部分和变体部分
| lim n → ∞ 变 体 部 分 主 体 部 分 = A ( ≠ 0 ) \lim_{n\to \infty}\frac{变体部分}{主体部分}=A(\neq0) limn→∞主体部分变体部分=A(=0) | 两部分为同量级 | 用定积分定义 |
| lim n → ∞ 变 体 部 分 主 体 部 分 = 0 \lim_{n\to \infty}\frac{变体部分}{主体部分}=0 limn→∞主体部分变体部分=0 | 两部分为次量级 | 用夹逼定理 |
按照汤老师的说法,用“齐与不齐”的概念进行理解,但当变体部分为 ln x \ln{x} lnx 时,便不再适用,如下题所示
这里今后采用武的方法

📚 1.1 第一节 函数 📚
函数的性态是这一节的重点
🏳️🌈 1.1.1 函数的概念及常见函数
(一)函数概念
1、分段函数
分段函数是一个函数,不能认为每一段是一个函数,也不能认为是多个函数
(1)绝对值函数
(2)符号函数
(3)取整函数
【注】取整函数的基本不等式: x − 1 < [ x ] < = x x-1<[x]<=x x−1<[x]<=x.
(4)狄利克雷函数
(二)复合函数
(三)反函数
【注】
(1)不是所有的函数都有反函数.
(2)单调函数必有反函数,反之不对.
(3)
y
=
f
(
x
)
y=f(x)
y=f(x) 的反函数为
x
=
f
−
1
(
y
)
x=f^{-1}(y)
x=f−1(y) ,也可写成
y
=
f
−
1
(
x
)
y=f^{-1}(x)
y=f−1(x) 。在同一直角坐标系中,
y
=
f
(
x
)
y=f(x)
y=f(x) 和
x
=
f
−
1
(
y
)
x=f^{-1}(y)
x=f−1(y) 的图形重合;
y
=
f
(
x
)
y=f(x)
y=f(x) 和
y
=
f
−
1
(
x
)
y=f^{-1}(x)
y=f−1(x) 的图形关于直线
y
=
x
y=x
y=x 对称.
(4)
f
−
1
[
f
(
x
)
]
=
x
f^{-1}[f(x)]=x
f−1[f(x)]=x ,
f
[
f
−
1
(
x
)
]
=
x
f[f^{-1}(x)]=x
f[f−1(x)]=x.
(四)初等函数
🏳️🌈 1.1.2 函数的性态
(一)单调性
(二)奇偶性
2、判定
可见,本题中偶函数的展开式中只有偶次项,没有奇次项,因为奇次项的导数都是奇函数,所以其奇次项导数都为零
【真】
偶函数的展开式只有偶次项,同样,奇函数的展开式只有奇次项,因为奇函数的偶数阶导函数在x=0处都为零
【小结】
偶函数在零点的展开式只有偶次项;
奇函数在零点的展开式只有奇次项。


tttt 【常见的奇(偶)函数】
(三)周期性
1、定义

2、判定

【小结】
- 函数的周期性与导函数的周期性之间的关系
- 函数的周期性与原函数周期性之间的关系
(四)有界性
1、定义
2、判定
【注】
能够用定义判定有界性的函数,往往是比较简单的函数,复杂的函数通常不能用有界性判定
【注】
(1)如果没有指明
x
x
x 的范围,而说“
f
(
x
)
f(x)
f(x) 为有界函数”,是指
f
(
x
)
f(x)
f(x) 在其定义域上为有界函数.
🏳️🌈 1.1.3 常考题型与典型例题
这里的重点是函数性态
📘 题型一 复合函数
早期常考,如今考得较少
🖊【例】
描述:本题属于复合函数的概念型问题,需要理解定义域的含义
【题结】
需要理解定义域的确定范围,定义域指的是自变量的取值范围;
而复合函数中,自变量只是括号中未知数的部分,而不是整个括号内部,勿混淆
🖊【例】
描述:需要注意复合函数的定义域的准确确定
🖊【例】
描述:该类题型需要理清并固定自己的解题步骤,不然算着算着就绕进去了,淦
🖊【真】
🖊【真】
📘 题型二 函数性态⭐️
常考函数有界性、单调性、周期性及奇偶性的判定
【例】
【例】
【例】
【例】
📚 第二节 极限 📚
极限是研究函数的工具,是第一章的重难点

极限的核心内容就三个,这三个属于概念理论,这里出题较多的是选填,或是证明题
再下面就是极限的两个极端状态

实际上很多重要的概念都和无穷小密切相关,如:
导数是两个无穷小之比的极限
积分是无穷项无穷小的和
🏳️🌈 1.2.1 极限的概念
这里所的极限一般分为函数极限和数列极限
1、数列极限
2、函数极限
函数极限与数列极限类似,但函数极限在趋向无穷时有三种
[自变量趋于无穷时]
[自变量趋于有限值时函数的极限]
🏳️🌈 1.2.2 极限的性质
虽说极限性质有很多条
但是核心只有三条
其中,保号性又是三大性质里面的重点
数列极限有对应的下列三条性质
| 局部有界性 | ||
| 保号性 | ||
| 函数值与极限值之间的关系 |
1、局部有界性
2、保号性
(1)保号性
注:保号性强调的是去心邻域!!!
注意两个方向的等号取舍
(2)保序性
保序性为保号性的推广
注:
① 由极限推函数,需要严格按照保序性,
即只有恒正(负)推恒正(负),不可带有等号
② 由函数推极限,无论函数是正,还是恒正,所推得的极限都带等号例题(参《660》,125)
如(1/n)大于0,但其极限等于0
3、函数值与极限值之间的关系
或称为极限值与无穷小之间的关系,总之记住以下的式子
🏳️🌈 1.2.3 极限的存在准则
常用于数列,这里以数列为例,函数极限同样也有下面两个准则
1. 夹逼准则
【思考】
夹逼准则一定要求是闭区间吗
【答】开闭均可,只是闭区间更宽泛,使用范围广
2. 单调有界准则
单调有界准则需要分别证明单调、有界;
但顺序随意;
单调性:
常选择后项减前项的方法;
若单调减,则进一步证明有下界,
若单调增,则进一步证明有上界;
此外,在使用放缩时,
有下界常缩小;
有上界常放大
【取舍】
》遇到n项和的极限,或者极限容易求得的,常选用夹逼准则,因为n项和不是有限项,不能一项一项去算,需要整体算
》遇到递推关系,或是极限不容易求得的,常选用单调有界准则(当这样的题一旦出现,一般是最难的题,或者说第二难的题)
这种题一般两步
s1:证极限存在(用单调有界准则)
s2:令A=f(A),解方程即可
🏳️🌈 1.2.4 无穷小量
无穷小和无穷大是极限的两个极端状态
1、无穷小的概念
2、无穷小的比较
3、无穷小的性质
无穷小的三大基本性质
🏳️🌈 1.2.5 无穷大量
无穷小量和无穷大量是极限的两个极端状态
1、无穷大的概念
2、常用的一些无穷大的比较
不同于无穷小量,无穷大没有同阶、高阶、等价这些概念;
但是“无穷大量的比较”这样的问题是存在的
》无穷级数的敛散性判定,常用到以下结论,需熟记
3、无穷大与无界变量的关系
这是两个有关,但又有本质区别的两个概念
4、无穷大量与无穷小量的关系
1 0 \frac{1}{0} 01 是一个没有意义的表达式
【T】
【极限的乘法法则】
极限的乘法法则使用条件是有限个极限的乘积;
对于无限的极限的乘积没有这种说法
🏳️🌈 1.2.6 常考题型与典型例题
围绕着五个知识点,这里的考题主要有四类题型
| 1 | 题型一 极限的概念性质及存在准则 | |
| 2 | 题型二 求极限 | |
| 3 | 题型三 确定极限式中的参数 | |
| 4 | 题型四 无穷小量 阶的比较 |
📘 题型一 极限的概念、性质及存在准则
此处考察概念理论,多为选择题或证明题,为难点
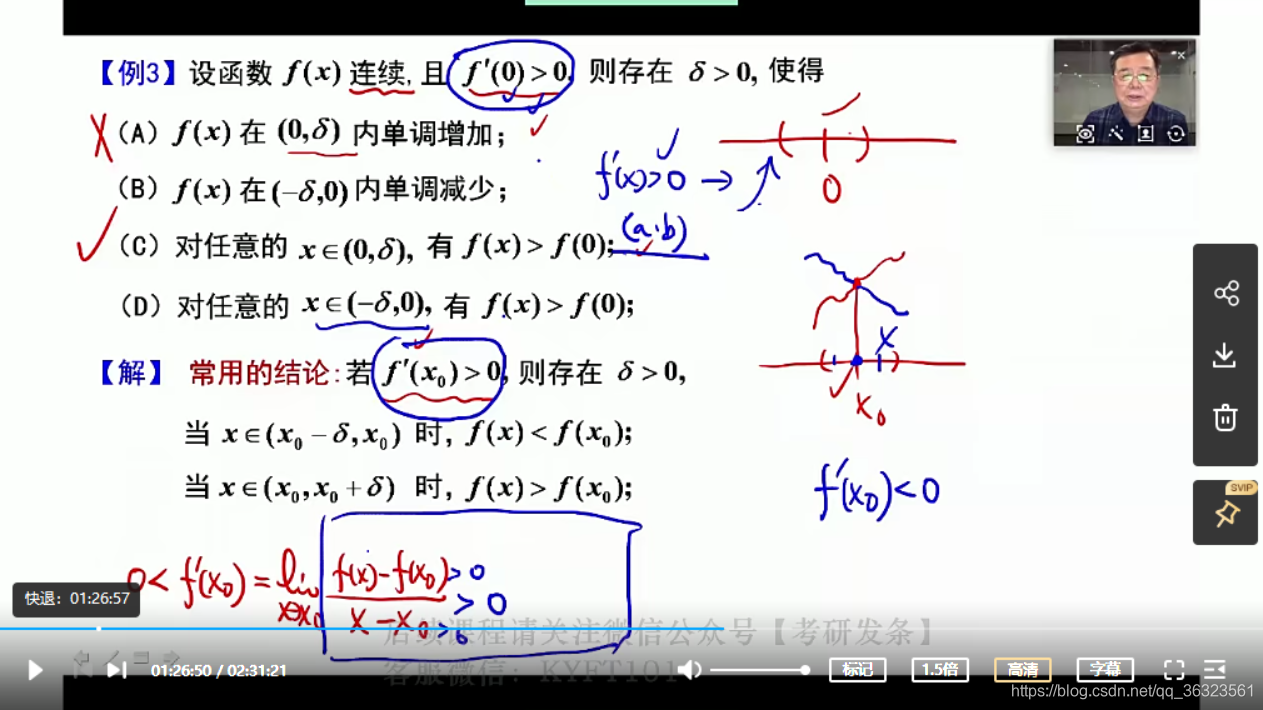
【例】
基础班所讲的结论
【例】
本题意在考察保序性,但保序不能保所有项,因为前面项管不了,只能保n充分大时的情况
【例】
【例】
本题主要考察单调有界准则
【真】
📘 题型二 求极限⭐️⭐️⭐️
重点,但非难点,内容较多,属于方法型问题
此处注意归纳
① 求极限的常见方法(8种);
② 求极限的常见题型
| 一 | 求极限的常用方法 | |
| 二 | 求极限的常见题型 |
一、求极限的常用方法
(一)利用有理运算法则求极限
本题利用已知的结论,甚至不用考虑单调增减这一条件
(二)利用基本极限求极限

(三)利用等价无穷小代换求极限
常用等价无穷小
常用等价无穷小补充:
【例】
(四)利用洛必达法则求极限
能不能用,用了再说。
当使用后极限存在(包括0)或极限为无穷时,此时结果有效;
若使用后极限存在,说明洛必达使用无效,需要其他方法验证。
因为洛必达定理是由柯西中值定理证明所得,故要求分母的导数非零
(五)利用泰勒公式求极限
泰勒公式有两种,
一种是皮亚诺余项;
一种是拉格朗日余项
但是在求极限中,因为极限是函数的局部性态,所以求极限用的是局部泰勒公式(即皮亚诺余项的泰勒公式)
【例】
(六)利用夹逼准则求极限
使用夹逼的思想是:
一个极限不好计算,通过放缩使得其便于计算
比如说不能合成简单表达式的n项和,因为不能一项一项计算,所以通过将分母换成一样的进行放缩,结合使用夹逼简化计算
这里会见到各种不等式,需熟练使用不等式的应用-
(此处整理不等式)
【例】
【题】
描述:
其他知识点:本题要求熟练使用不等式
(七)利用定积分定义求极限
提取可爱因子
实际上也可用夹逼,不过不同于上面的那种
(八)利用单调有界准则求极限
常见于递推关系求极限,往往有两步
s1:证明极限存在
s2:令成A计算
虽然题目要求直接求极限,但仍需要先证明极限存在;
倘若不证明极限存在而直接求极限,有时所得极限并非是真正的极限(可以证明)
(九)利用中值定理求极限
这里的包括微分中值定理和积分中值定理
【例】
本题虽可用泰勒,但慢了
在使用中值定理时,不用管 ξ \xi ξ 的上下限谁大谁小,夹逼夹就完了
(十)T
含有根式通常想到有理化
二、求极限的常见题型
平时所见的极限问题,可分为两大类
函数极限
数列极限
(一)函数的极限


【例】
根式差可用有理化的方法,但局限性较高,当开方大于2时,更好的方法是利用公式等价代换、或拉格朗日中值定理
【例】
这种e-e的类型也可选择拉格朗日中值定理这种方法
【例】
本题常用手段是泰勒,但可创造条件使用等价代换
实际上不觉得比泰勒方便多少,同样都是记忆公式,相反,记住泰勒可直接推出相关的等价代换公式
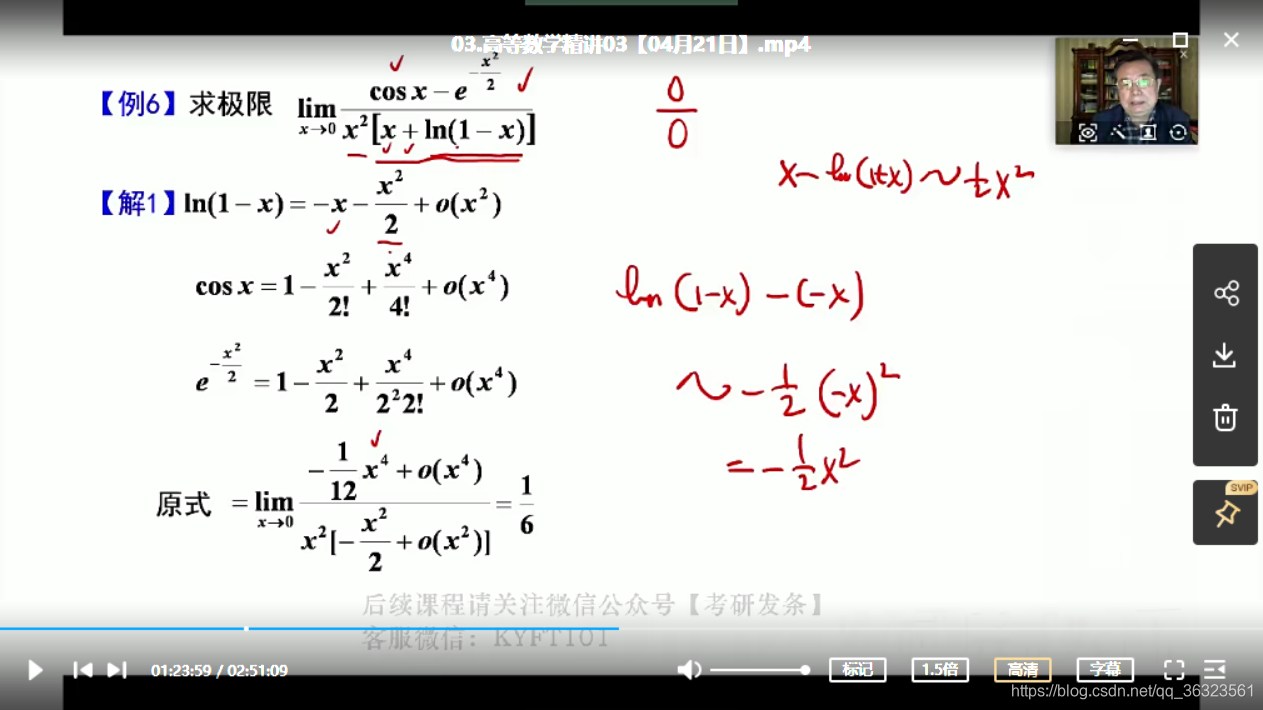
【例⭐️】
本题说明处理0比0型变上限积分不一定需要洛必达,可用变上限积分的相关等价代换
【例】
【例】
【例2】
若为选填题,可直接看带头大哥
若为解答题,必须先同除
【例】
【例】

【例3】
【例】
除了使用有理化的方法,也可以用“提无穷因子的方法”
【例】
想通分却没有分母,可以选择做倒代换(目的是人为制造分母)不过还是慢了
进一步可选用泰勒
方法三:提无穷因子,用等价代换
【例】
2020年有一题求渐近线的题目,核心就是求下列极限
4、利用递推关系
此处是出难题的考点,一般压轴题都是在这里出题
【例】
两种方法求递推关系
【例】
本题采用多种方法证明了 { x n } \{x_n\} {xn} 存在,可多多参考
(2)中注意,数列极限不可用洛必达,需要转化
【例】
》题结
① 由递归函数单调减,判断数列不单调,从而选择方法二先斩后奏
② 一般在处理 ∣ x n − a ∣ |x_n-a| ∣xn−a∣ 时,都是直接代入 a a a 的值;本题由于 a a a 非简单值,故不适合直接代入 a a a 值
【例】
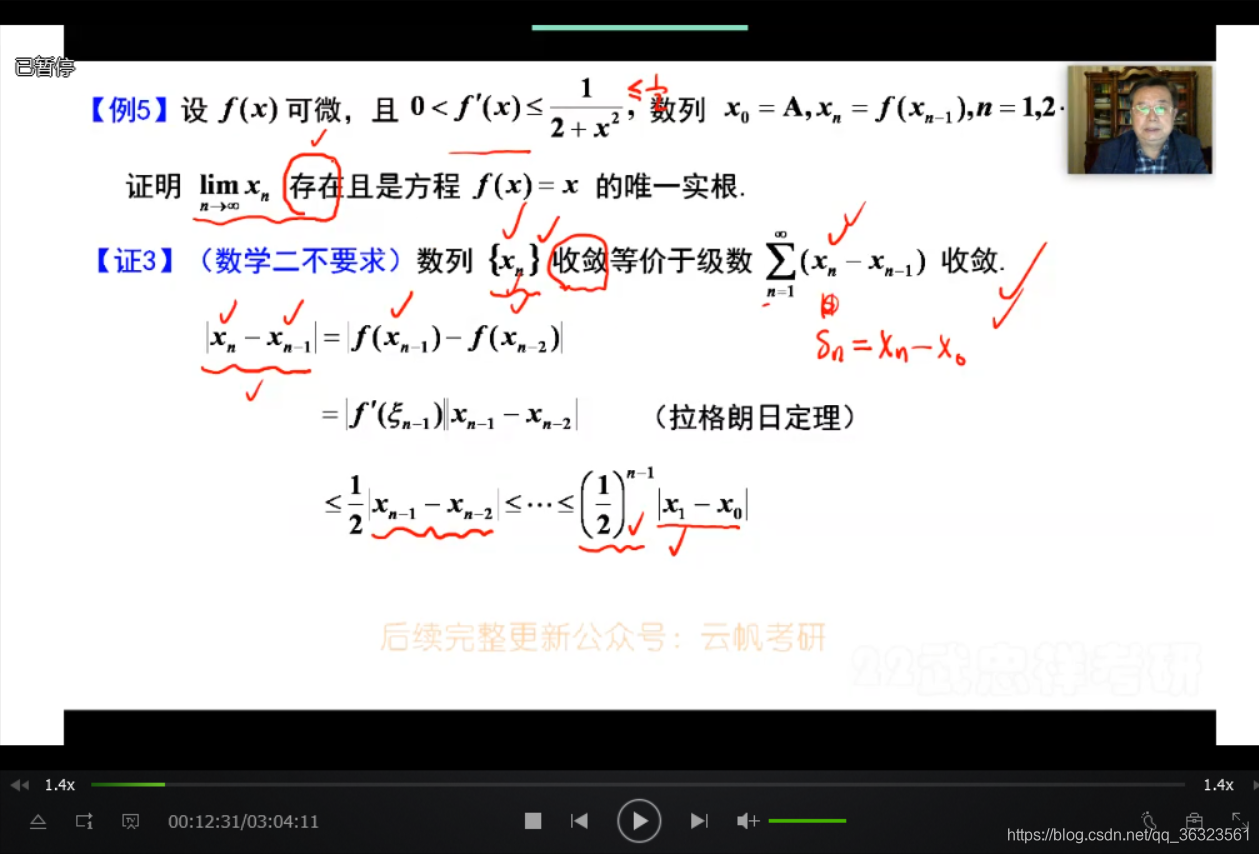
例5的综合性更强
再证明极限存在时,本题用了三种典型的方法以供参考
解法一:利用单调有界准则
解法二:利用定义,直接证明 x n {x_n} xn 有极限
解法三:证明数列收敛,等价于证明对应的级数收敛,利用级数收敛的结论证明数列收敛解法一:结合牛顿莱布尼兹公式,建立原函数与函数之间的关系
解法二:先斩后奏
解法三:
由递推关系函数单调增,只能得数列是单调的,至于是增是减,需要由 x 1 、 x 2 x_1、x_2 x1、x2 的大小进一步比较;
本题 x 1 、 x 2 x_1、x_2 x1、x2 大小比较未知,故需要证明出数列同时具有上下界。
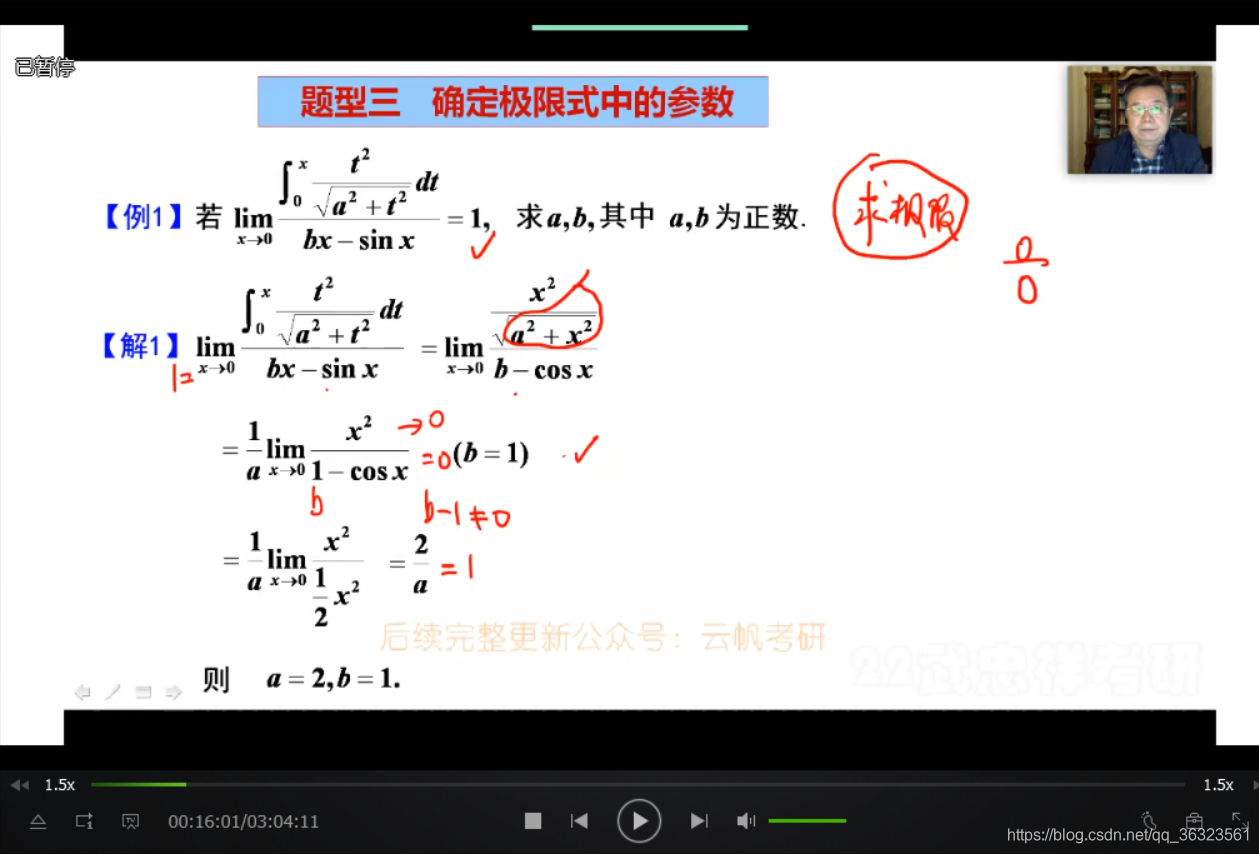
📘 题型三 已知极限确定参数
虽然说是一种单独的题型,但核心仍是求极限
【例】
描述:已知极限,确定参数
方法:求极限确定参数
解法一:
解法二:(变上限积分的等价代换)
【例】
》解题方法同样是求极限,在求极限的过程或者结果中确定参数
》出现根式,传统的一般思想就是有理化
解法一:传统方法有理化(本题非最优解)
解法二:
》分别确定不同的参数
》无穷减无穷的解题思想:
往外提无穷因子
》虽然后续仍有有理化,但较为简单
解法三:
【例】
n次根式常用方法是提无穷因子,用等价代换
【例】
例四自己看
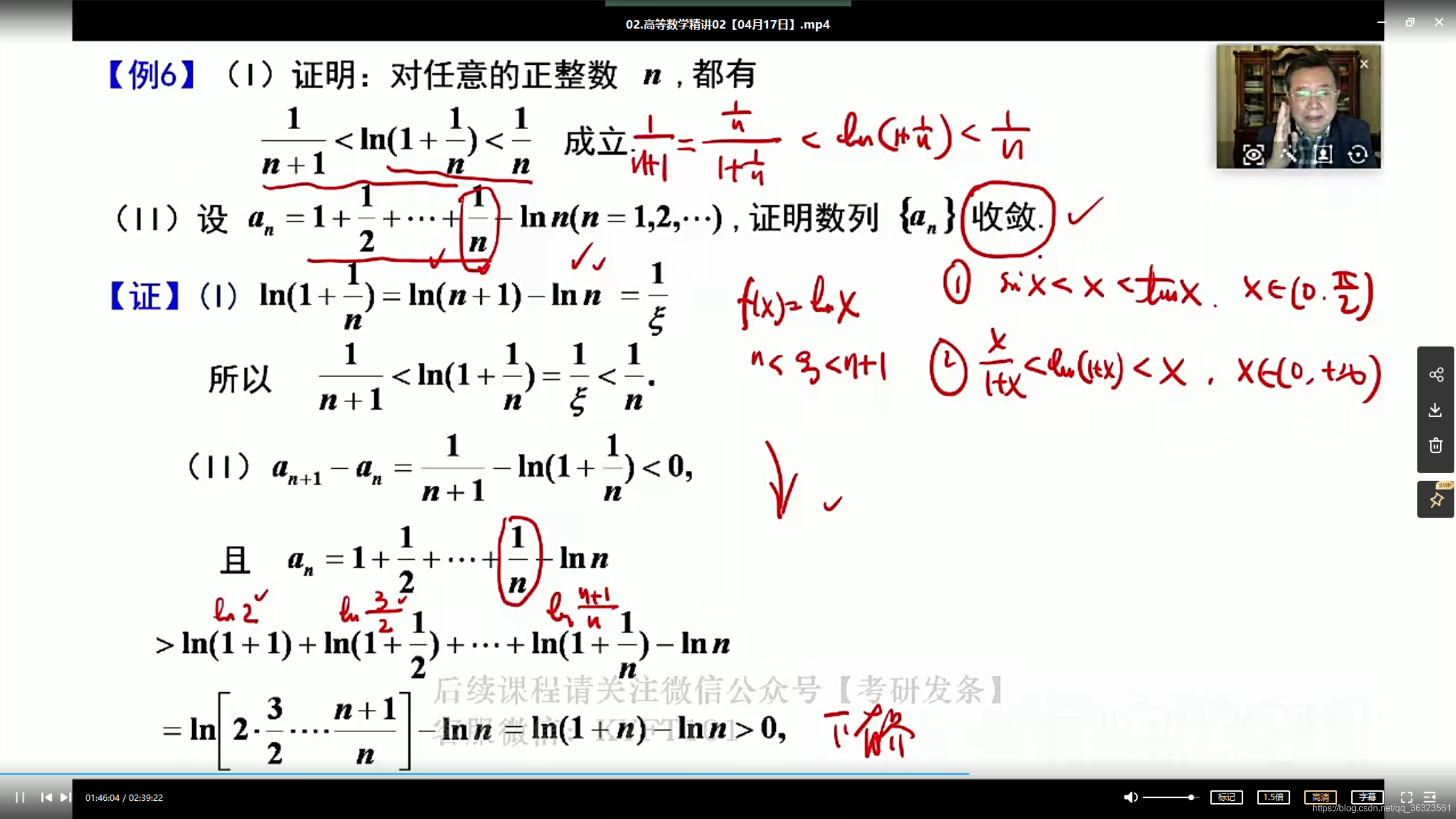
📘 题型四 无穷小量阶的比较⭐️⭐️⭐️
实质是0比0的极限问题,所以仍然可以认为是极限问题(可见求极限的重要性)
【例】❗️❗️ 记结论
》排序问题
》核心思想方法有两个
① 两两比,用定义(本题不适合)
② 定阶
【例】
属于:无穷小比阶问题
无穷小比阶问题,需依次估计出每个无穷小的阶数再比较(求极限仍是核心)
【例】
已知极限确定参数
洛必达和泰勒是在所有实数中找未知参数,如同大海捞针,效率不高
》选择题通常可用排除法(代入法)
【例】
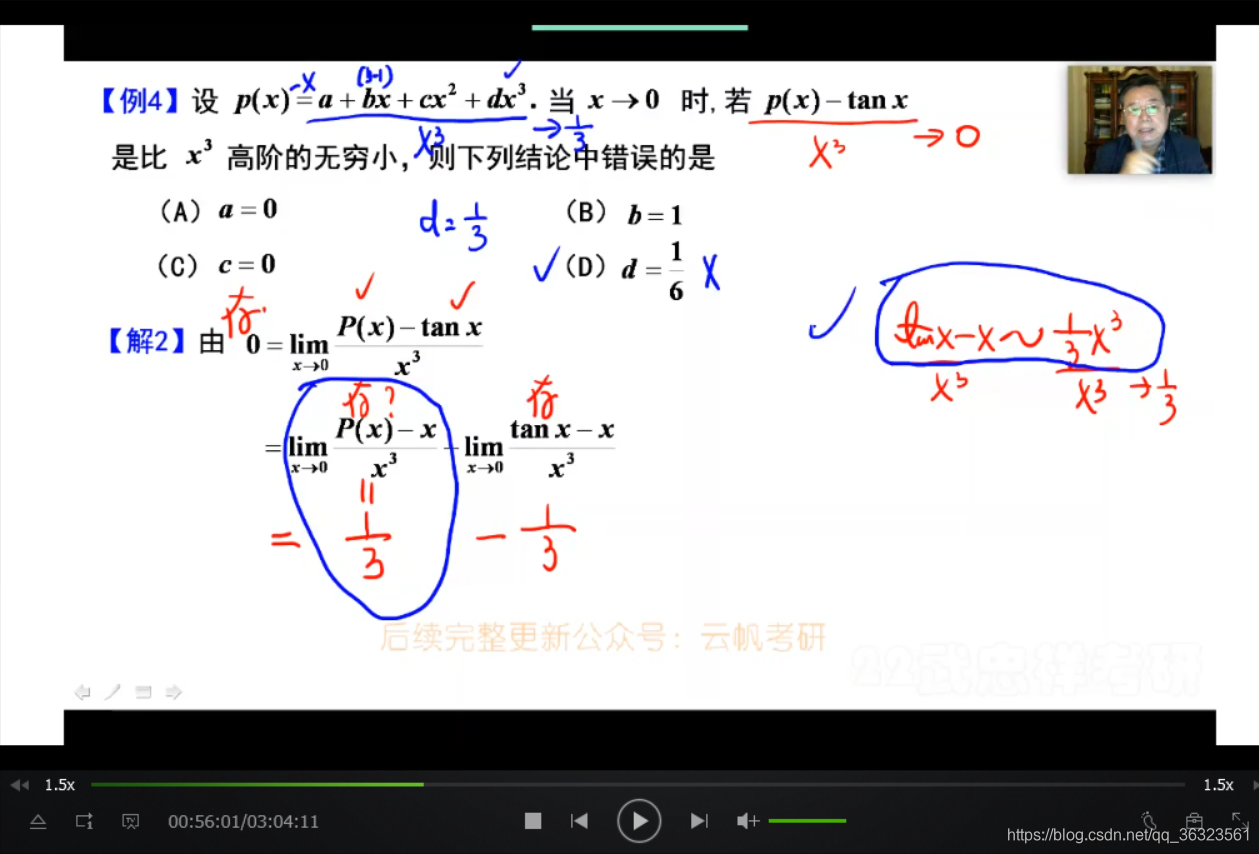
0比0就三种方法,具体用哪一种
① 用洛必达,四个参数太繁琐
② 用泰勒,将一般函数写成多项式(可选,但本题非最优)
注:对极限中出现多项式函数(如本题 p ( x ) p(x) p(x)),求一大堆系数时,首选泰勒
解法二:(创造条件)
【例】❗️❗️
本题为0比0,但洛必达不合适;
而等价代换也不满足条件;
故选择方法三:泰勒
解法二:(排除法)
偶函数在0点处的泰勒展开式只有偶次项,故n只能为偶数
【小结】
注意方法二的技巧,需要对泰勒公式的熟练理解
*1.2.7 题
【例】
该题用到后面的拉格朗日中值定理,也是求极限常用的方法之一
该题不一定需要用拉格朗日中值定理,在展开式掌握熟练的情况下,可更简便地解题
【T】
【海涅定理相关】
📚 第三节 函数的连续性 📚
🏳️🌈 1.3.1 连续的概念
【连续的概念】
🏳️🌈 1.3.2 间断点及其分类
1、间断点的概念
【注意】:
间断点的前提是在去心邻域有定义,在一点处可以无定义,但在邻近需要有定义;
不能说“不连续的就是间断点”
2、间断点的分类
基于左右极限是否都存在分为两类:
第一类间断点
第二类间断点
【注】:
第一类间断点只有上面两种;
而第二类间断点不止上面两种。
4、求间断点
见 题型一
3、T
- 若两个函数在某区间内均连续,则其两函数的复合函数在该区间也连续【《660题》141】
🏳️🌈 1.3.3 连续函数的性质
连续函数的性质一般是指闭区间上的性质
闭区间连续函数有四大性质,分别为:最值定理、有界性定理、介值定理、零点定理 。
【连续函数的运算性质】
注意:“2)”中是定义区间而非定义域
【最值定理】
【有界性定理】
【介值定理】
【条件】
- 取值区间为闭区间
【零点定理】
[Notes]
介值取值区间为开区间
》零点定理是介值定理的特例,但由于使用频繁,故可平起平坐
[描述]
- 闭区间连续
- 两端点异号
[用途]
可用于证明方程的根的存在性
🏳️🌈 1.3.4 常考题型与典型例题
📘 题型一 讨论连续性及间断点的类型⭐️⭐️⭐️
——》关于 {间断点类型的出题形式}:
有以下几种:
1、常规函数找间断点判定类型
2、函数变化量,带有绝对值
3、 f ( x ) f(x) f(x) 未知,由极限式给出
——》关于 {如何确定间断点的位置}:
主要是找可疑点,而可疑点又有两种:
① 无定义点
② 分段函数的端点
【例1】
【例2】
【例3】
》本题属于常考的经典题型
》不过今后不再考察大题,会出现在选填中
》讨论连续性,看无定义点,无定义点肯定不连续
初等函数在其 定义区间 (非定义域)处处连续,本题在排除了无定义点后,其余均属于该初等函数的定义区间,故处处连续。
》求极限有三种情况需要分左右:
① 分段函数分界点
② e ± ∞ e^{\pm\infty} e±∞
③ arctan ± ∞ \arctan\pm\infty arctan±∞
【例4】
高频考题
【例6】
【note】
偶函数的间断点也对称
【题1】
《660题》No.141
【T】
注意事项:
- 在间断点问题中,找可疑点需要找全,如:
tan x \tan{x} tanx中也包含可疑点
📘 题型二 介值定理、最值定理及零点定理的证明题
这种证明题不会单独直接考;
会结合后面的微分中值定理的综合证明题
【例】
【例】
本题考查零点定理
构造辅助函数,用零点定理
>【注意与下一题的联系】
【例⭐️】
【注意与上一题的联系】
和上一题相比,本题同样是闭区间连续,但不同的是在区间内并不是恒正或恒负
》本题同样需要构造辅助函数,但是要验证两端点异号比较困难;
题干中看到 “ 1 4 \frac{1}{4} 41” 可考虑将区间四等分,通过区间内的各个点处的和为零,判断构造函数在该区间内是恒正、恒负、还是存在零点,从而完成解题
》关于{判断恒正恒负}
一般情况需分两情况讨论:
① 存在函数值为零时,需证明这四个点处至少有一点函数值为零,则得证
② 函数值均不为零时,需证明这四个点处函数值都不为零,又因为和为零,可推里面存在异号,可进一步使用零点定理得证
实际上进阶的方法是用反证法,可避免讨论这两种情况
》进一步,证明非 “ 1 4 \frac{1}{4} 41” 而是 “ 1 n \frac{1}{n} n1” ,则是将区间分为 n n n 等份,再从0开始代入n个点,之后相加等于零,判断零点,完成解题【回头自己证】
【例】
显然是证明构造函数在区间上有零点的题型,用零点定理
》使用零点定理需两个条件:
① 连续
② 两端点异号
T
@
一元的基本初等函数在其定义域内连续
一元的初等函数在其定义区间内连续

















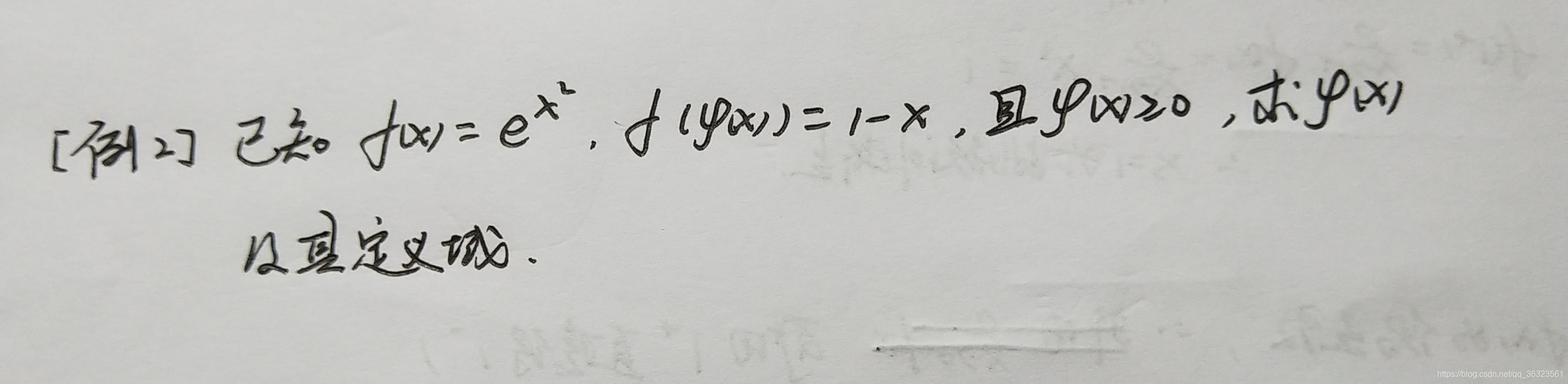


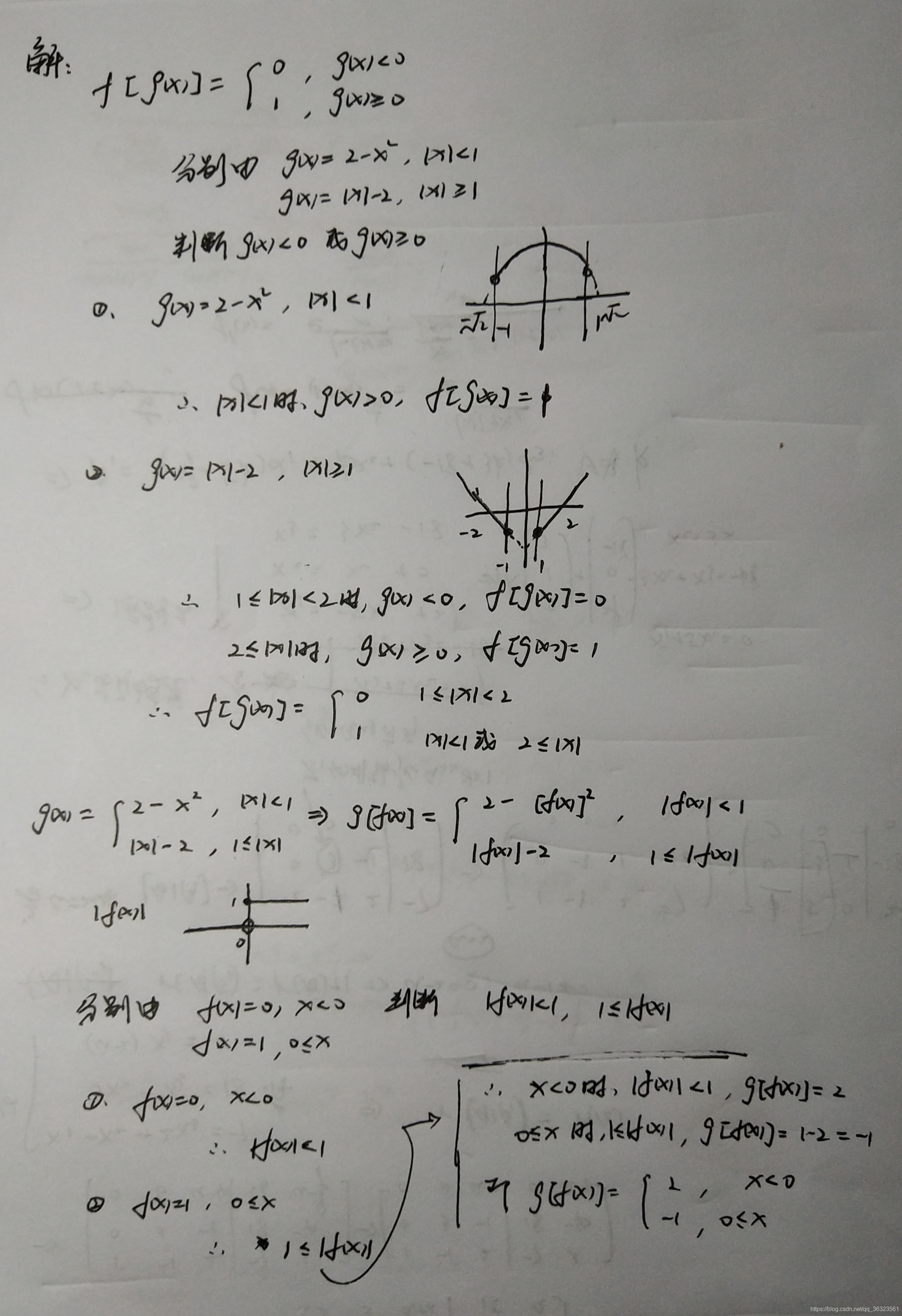

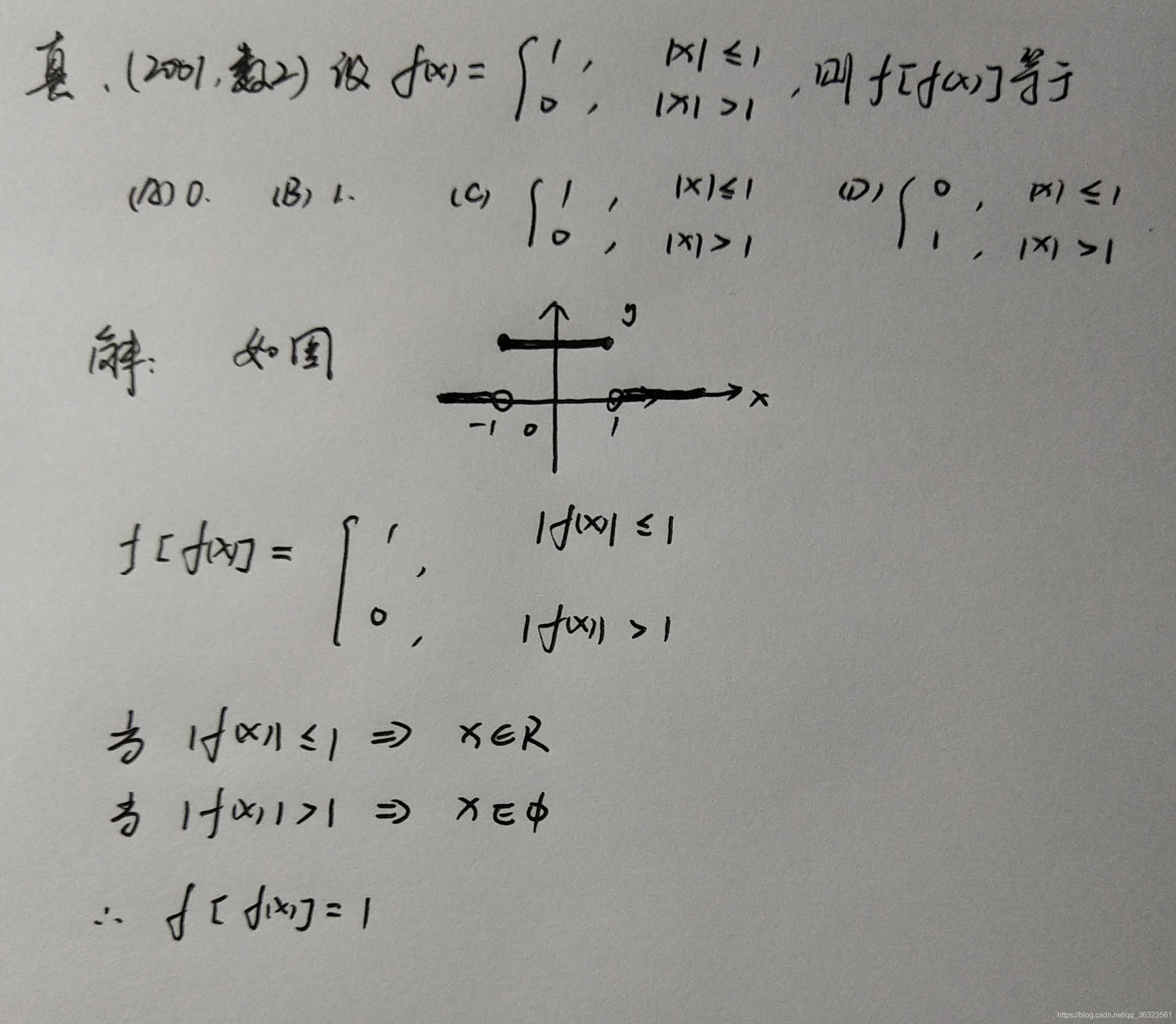




















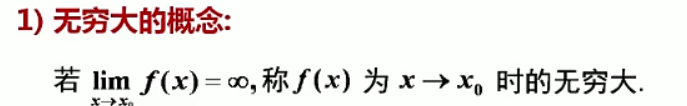
















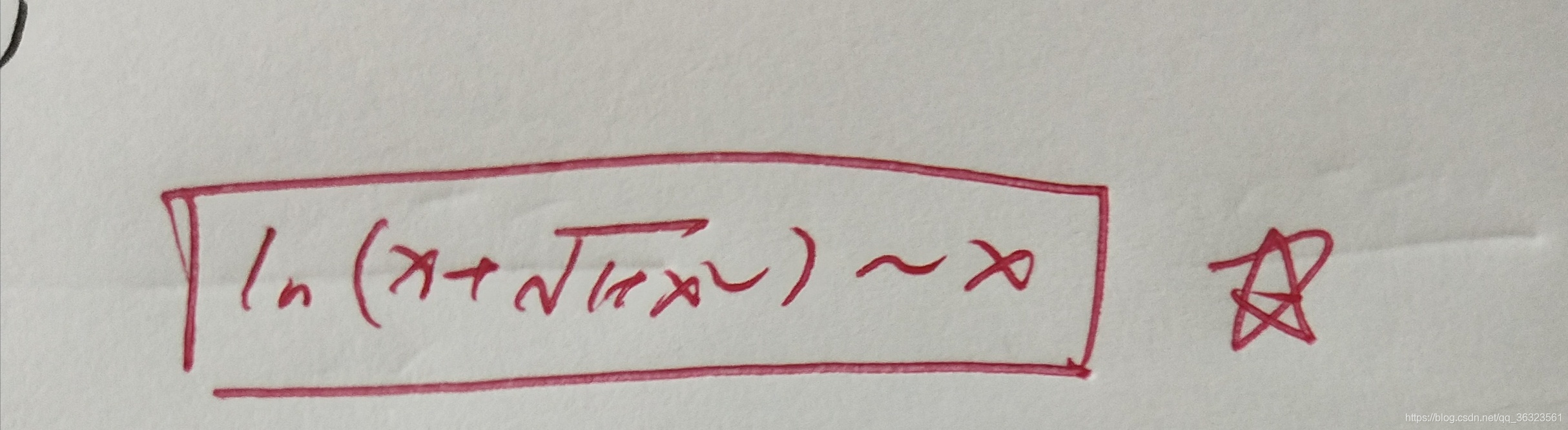
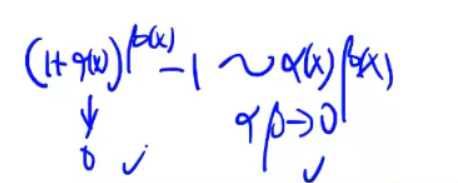





























































































 4213
4213

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








