梯度下降---偏导数及其几何意义

在一元函数中，我们已经知道导数就是函数的变化 率。对于二元函数我们同样要研究它的“变化率”。然

而，由于自变量多了一个，情况就要复杂的多。

一、几何意义

　　在xOy平面内，当动点由P(x0,y0)沿不同方向变化时，函数f(x,y)的变化快慢一般说来是不同的，因此就需要研究f(x,y)在(x0,y0)点处沿不同方向的变化率。

   偏导数表示固定面上一点的切线斜率

假设ƒ是一个多元函数。例如：

。

f = x² + xy + y²的图像。

我们希望求出函数在点（1, 1, 3）的对x的偏导数；对应的切线与xOz平面平行。

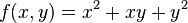因为曲面上的每一点都有无穷多条切线，描述这种函数的导数相当困难。偏导数就是选择其中一条切线，并求出它的斜率。通常，最感兴趣的是垂直于y轴（平行于xOz平面）的切线，以及垂直于x轴（平行于yOz平面）的切线。

这是图中y = 1时的图像片段。

一种求出这些切线的好办法是把其他变量视为常数。例如，欲求出以上的函数在点（1, 1, 3）的与xOz平面平行的切线，我们把变量y视为常数。右图中显示了函数的图像以及这个平面。左图中显示了函数在平面y = 1上是什么样的。通过求出这个图中的切线，我们发现ƒ在点（1, 1, 3）的与xOz平面平行的切线的斜率是3。我们把它记为：

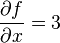
在点（1, 1, 3），或称“f在（1, 1, 3）的关于x的偏导数是3”。

二、定义

　　在这里我们只学习函数f(x,y)沿着平行于x轴和平行于y轴两个特殊方位变动时，f(x,y)的变化率。

　　偏导数的算子符号为:∂

　　偏导数反映的是函数沿坐标轴正方向的变化率。

设有二元函数z=f(x,y)，点(x0,y0)是其定义域D内一点.把y固定在y0而让x在x0有增量△x，相应地函数z=f(x,y)有增量(称为对x的偏增量)△z=f(x0+△x,y0)-f(x0,y0)。

　　如果△z与△x之比当△x→0时的极限存在，那么此极限值称为函数z=f(x,y)在(x0,y0)处对x的偏导数(partial derivative)。记作f'x(x0,y0)。

 y方向的偏导

　　函数z=f(x,y)在(x0,y0)处对x的偏导数，实际上就是把y固定在y0看成常数后，一元函数z=f(x,y0)在x0处的导数

　　同样，把x固定在x0,让y有增量△y,如果极限存在 那么此极限称为函数z=(x,y)在(x0,y0)处对y的偏导数。记作f'y(x0,y0)

　三、高阶偏导数

如果二元函数z=f(x,y)的偏导数f'x(x,y)与f'y(x,y)仍然可导，那么这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。  二元函数的二阶偏导数有四个：f"xx，f"xy，f"yx，f"yy.

　　注意：f"xy与f"yx的区别在于：前者是先对x求偏导，然后将所得的偏导函数再对y求偏导；后者是先对y求偏导再对x求偏导.当f"xy与f"yx都连续时，求导的结果与先后次序无关。