线性回归

最新推荐文章于 2025-03-15 17:16:44 发布

不论如何未来很美好

最新推荐文章于 2025-03-15 17:16:44 发布

阅读量918

点赞数 3

分类专栏：数据挖掘算法文章标签：线性回归

本文链接：https://blog.csdn.net/qq_36523839/article/details/82924705

版权

数据挖掘算法专栏收录该内容

36 篇文章

订阅专栏

线性回归：

简单描述就是通过线性方程（1次函数）去拟合数据点：

但是如何使用该线性方程去拟合数据点呢？我们能得到拟合的整体误差，即图中蓝色线段的长度总和。如果某一条直线对应的误差值最小，就代表这条直线最能反映数据点的分布趋势：

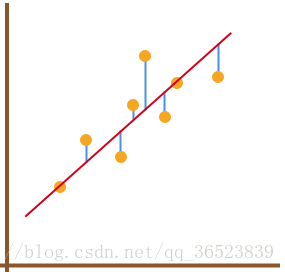
误差如何表示？在线性回归中，使用残差的平方和来表示所有样本点的误差（专业名称：平方损失函数）：

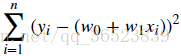
如何求解上面的平方损失函数？使用最小二乘法即代数求解，最小二乘法是用于求解线性回归拟合参数 w 的一种常用方法。最小二乘法中的「二乘」代表平方，最小二乘也就是最小平方。而这里的平方就是指代上面的平方损失函数。

通过对f（损失函数）求一阶偏导等处理后，得到如下结果：

所以w0、w1代码表示为：

  def w_calculator(x, y):
      n = len(x)
      w1 = (n*sum(x*y) - sum(x)*sum(y))/(n*sum(x*x) - sum(x)*sum(x))
      w0 = (sum(x*x)*sum(y) - sum(x)*sum(x*y))/(n*sum(x*x)-sum(x)*sum(x))
      return w0, w1

通过scikit-learn可以实现最小二乘法线性回归：

sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)

fit_intercept: 默认为 True，计算截距项。（即模型中的常数）
normalize: 默认为 False，不针对数据进行标准化处理。
copy_X: 默认为 True，即使用数据的副本进行操作，防止影响原数据。
n_jobs: 计算时的作业数量。默认为 1，若为 -1 则使用全部 CPU 参与运算。

矩阵运算：

在实际的情况下，我们运算的很多数据集都是呈矩阵的形式，所以这就涉及到将其转换为矩阵的运算：

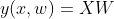
y(x,w) = XW

推导公式这里就不详说了，得到最终的矩阵公式：

$W = (X^{T}X)^{-1}X^{T}Y$

评价指标：

回归预测结果，通常会有平均绝对误差、平均绝对百分比误差、均方误差等多个指标进行评价

平均绝对误差（MAE）就是绝对误差的平均值，它的计算公式如下：

均方误差（MSE）它表示误差的平方的期望值，它的计算公式如下：

平均绝对百分比误差（MAPE），如果 MAPE 为 55，则表示预测结果较真实结果平均偏离 5：