堆详解

A Heap is a special Tree-based data structure in which the tree is a complete binary tree. Generally, Heaps can be of two types:

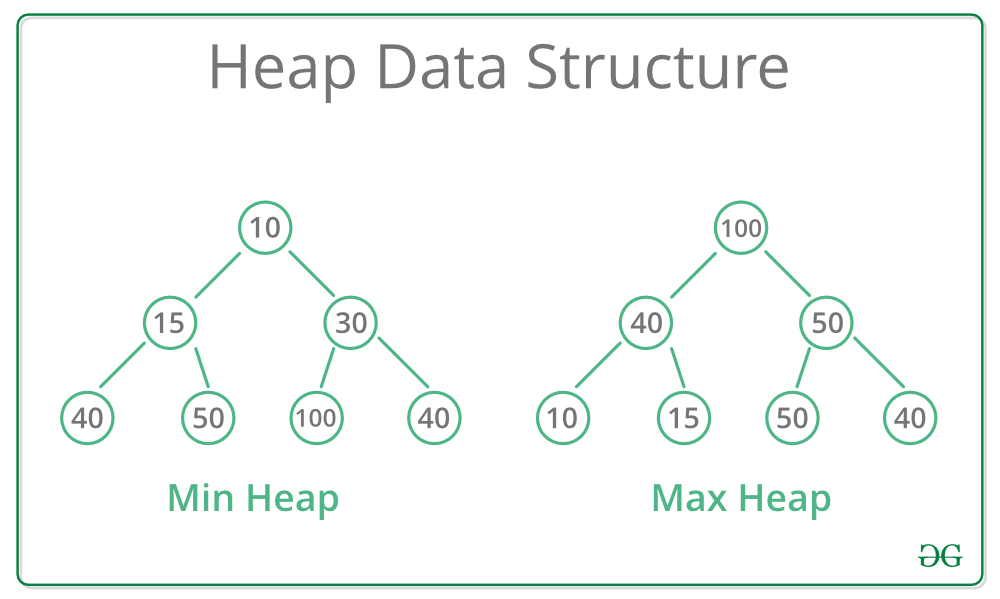
• Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
• Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.

堆是什么

堆是完全二叉树，且要么是最小二叉树，要么是最大二叉树

• 最大堆：父节点大于等于子节点
• 最小堆：父节点小于等于子节点
  

堆的表现形式

堆表现为一个数组

• 根节点：arr[0]
• 父节点：arr[(i-1)/2]
• 左子节点：arr[2*i+1]
• 右子节点：arr[2*i+2]

这样的设计让堆的层次遍历简单地成为了数组的顺序遍历
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MW3g4koN-1609559954464)(https://www.geeksforgeeks.org/wp-content/uploads/binaryheap.png)]

构建堆

以最大堆为例子，构建堆的时间复杂度为O(n)

def max_heapify_node(arr, n, i):
    largest = i
    l = 2*i + 1
    r = 2*i + 2

    # If left child is greater than parent
    if l < n and arr[largest] < arr[l]:
        largest = l

    # If right child is greater than smallest so far
    if r < n and arr[largest] < arr[r]:
        largest = r

    # If smallest is not parent
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]

        # Heapify the root
        max_heapify_node(arr, n, largest)

    return True


def max_heapify(arr, n):
    # Build a max heap
    for i in range(n//2-1, -1, -1):
        max_heapify_node(arr, n, i)
        
    return True


if __name__ == "__main__":
    arr = [54, 6, 1, 64, 4, 1, 3, 5]
    print(arr)
    max_heapify(arr,len(arr))
    print(arr)

输出：

(base) ~/.../manjaro_workspace/py100 >>> python test13.py                                                                                                                                                                       
[54, 6, 1, 64, 4, 1, 3, 5]
[64, 54, 3, 6, 4, 1, 1, 5]

堆的需要实现的基本操作

以最大堆为例子，除了堆的构建之外，一个堆需要实现以下基本操作

• get_max()：返回根节点值，由于堆的特性，最大堆的更节点值也就是其最大值，时间复杂度为O(1)。
• extract_max()：返回并删除根节点，由于在删除根节点之后需要对堆进行维护，维护堆的时间复杂度为O(logn)，所以这个操作的时间复杂度也为O(logn)，
• increase_key(key,value)：给key赋一个新值，此值需大于旧值，由于在进行此操作后同样要对堆进行维护，所以其的时间复杂度也是O(logn)
• insert(value)：在堆中插入一个元素，首先将值插入到堆尾部，然后对堆进行维护，时间复杂度为O(logn)
• delete(key)：删除堆内的一个元素，删除元素并对堆进行维护，时间复杂度为O(logn)

最大堆的一种实现

class MaxHeap:
    def __init__(self, arr=list()):
        self._arr = arr
        self._size = len(arr)        # Number of nodes
        self._heapify()        # Initialize the heap

    @property
    def size(self):
        """
        @description  :
            Get current heap size
        ---------
        @param  :
            Void
        -------
        @Returns  :
            Current heap size
        -------
        """
        return self._size

    @property
    def arr(self):
        """
        @description  :
            Get current heap arr
        ---------
        @param  :
            Void
        -------
        @Returns  :
            Current heap arr
        -------
        """
        return self._arr

    def get_max(self):
        """
        @description  :
            Get the heap's maximal element
        ---------
        @param  :
            Void
        -------
        @Returns  :
            The root element of heap
        -------
        """
        return self._arr[0]

    def extract_max(self):
        """
        @description  :
            Remove the maximal element of the heap
        ---------
        @param  :
            Void
        -------
        @Returns  :
            Deap's root element if exist or False
        -------
        """
        # If root element do not exist
        if self.size <= 0:
            return False
        # Considering the heap property
        # when deletation, delete the last element
        max_element = self.arr[0]
        self._size -= 1
        self._arr[0] = self.arr[self.size]
        self._arr.pop(self.size)

        # Maintain heap
        # Consiering the heap property, heap can be maintained by heapifying subtree
        self._heapify_subtree(self.size, 0)
        return max_element

    def increase_key(self, key, value):
        """
        @description  :
            Decrease the value of key.
        ---------
        @param  :
            key: Target key
            value: New-value = Old-value - value
        -------
        @Returns  :
            If fail, return Flase
            if success, return True
        -------
        """
        # Decrease operation
        self._arr[key] = self._arr[key] + value
        # Maintain the heap property
        self._maintain(key)
        return True

    def insert(self, value):
        """
        @description  :
            Insert operation takes two steps:
            1. Add new key at the end of the deap
            2. Maintain upward the deap
        ---------
        @param  :
            value: New key's value
        -------
        @Returns  :
            True if success
        -------
        """
        # Add new key at the end of the deap
        self.arr.append(value)
        self._size += 1
        # Maintain upward the deap
        self._maintain(self.size - 1)

    def delete(self, key):
        """
        @description  :
            Deletion operation takes two steps:
            1. Assign the root value to the key
            2. Extract the root value
            And the heap property will be maintained in the Extract operation
        ---------
        @param  :
            key: Target key
        -------
        @Returns  :
            True if success
        -------
        """
        self._arr[key] = self.arr[0]
        self.extract_max()
        return True

    def _maintain(self, key):
        """
        @description  :
            Maintain upward the heap
        ---------
        @param  :
            key: Beginning key
        -------
        @Returns  :
            True if success or raise Execption
        -------
        """
        # If key do not exist
        if key > self.size:
            raise KeyError("key do not exist")
        # If key is root
        if key == 0:
            return True
        # Maintain upward the heap
        parent = (key - 1) // 2        # parent element
        largest = self._heapify_subtree(self.size, parent)
        if largest != parent:
            self._maintain(parent)
        return True

    def _heapify_subtree(self, _size, i):
        """
        @description  : 
            Max-heapify a subtree
        ---------
        @param  : 
            _size: A subtree's arr size
            i: A sequence number of the subtree
        -------
        @Returns  :
            If success, return the largest key
        -------
        """
        largest = i     # Initialize the largest as parent
        l = i*2 + 1     # The left child node
        r = i*2 + 2     # The right child node

        # If left child exist and is greater than parent
        # assume left child is the largest
        if l < _size and self._arr[largest] < self._arr[l]:
            largest = l

        # If right child exist and is greater than parent
        # assume right child is the largest
        if r < _size and self._arr[largest] < self._arr[r]:
            largest = r

        # change parent if needed
        if largest != i:
            self._arr[i], self._arr[largest] = self._arr[largest], self._arr[i]

            # Recursively heapify the affected subtree
            self._heapify_subtree(_size, largest)

        return largest

    def _heapify(self):
        """
        @description  :
            Maxheapify the whole tree
        ---------
        @param  :
            Void
        -------
        @Returns  :
            True if success
        -------
        """
        number_minimal_subtree = self.size // 2
        for i in range(number_minimal_subtree - 1, -1, -1):
            self._heapify_subtree(self.size, i)
        return True


if __name__ == "__main__":
    arr = [54, 6,  64, 4, 1, 3, 5, 4, 6]
    print("初始数据：{}".format(arr))
    max_heap = MaxHeap(arr)
    print("堆化：{}".format(max_heap.arr))
    max_element = max_heap.extract_max()
    print("最大数：{}；取出最大数后：{}".format(max_element, max_heap.arr))
    increasing_key = 2
    increment = 100
    increasing_value = max_heap.arr[increasing_key]
    max_heap.increase_key(increasing_key, increasing_value)
    print("值增加{}的数：{}；增加后：{}".format(increment, increasing_value, max_heap.arr))
    new_element = 54
    max_heap.insert(new_element)
    print("插入数据：{}；插入后：{}".format(new_element, max_heap.arr))
    deleting_key = 0
    deleting_value = max_heap.arr[deleting_key]
    max_heap.delete(deleting_key)
    print("删除数据：{}；删除后：{}".format(deleting_value, max_heap.arr))

输出：

(base) ~/.../manjaro_workspace/py100 >>> python test14.py                                                                                                                                                                       
初始数据：[54, 6, 64, 4, 1, 3, 5, 4, 6]
堆化：[64, 6, 54, 6, 1, 3, 5, 4, 4]
最大数：64；取出最大数后：[54, 6, 5, 6, 1, 3, 4, 4]
值增加100的数：5；增加后：[54, 6, 10, 6, 1, 3, 4, 4]
插入数据：54；插入后：[54, 54, 10, 6, 1, 3, 4, 4, 6]
删除数据：54；删除后：[54, 6, 10, 6, 1, 3, 4, 4]

堆的应用

排序

以最大堆来说，其父节点总是大于其子节点，其根节点总是最大的，在数组里面其根节点对应就是数组里面第一个值，可以根据这个特性，对其进行排序，具体做法为将堆根部的数放在数组末尾，然后排除这个最大值对根节点进行最大堆化，循环这个操作就可得到排序后的数据，其时间复杂度为O(nlogn)。

def max_heapify_node(arr, n, i):
	largest = i
	l = 2*i + 1
	r = 2*i + 2

	# If left child is greater than parent
	if l < n and arr[largest] < arr[l]:
		largest = l

	# If right child is greater than smallest so far
	if r < n and arr[largest] < arr[r]:
		largest = r

	# If smallest is not parent
	if largest != i:
		arr[i], arr[largest] = arr[largest], arr[i]

		# Heapify the root
		max_heapify_node(arr, n, largest)

	return True


def max_heapify(arr, n):
	# Build a max heap
	for i in range(n//2-1, -1, -1):
		max_heapify_node(arr, n, i)

	return True

def max_heap_sort(arr):
	n = len(arr)
	max_heapify(arr, n)

	# One by one extract elements
	for i in range(n-1, 0, -1):
		print("\n==================")
		print(arr)
		arr[i], arr[0] = arr[0], arr[i]
		print(arr)
		max_heapify_node(arr, i, 0)
		print(arr)
		print("==================\n")

	return arr


if __name__ == "__main__":
	arr = [54, 6, 1, 64, 4, 1, 3, 5]
	print(arr)
	arr = heap_sort(arr)
	print(arr)

输出：

(base) ~/.../manjaro_workspace/py100 >>> python test13.py                                                                                                                                                                       
[54, 6, 1, 64, 4, 1, 3, 5]

==================
[64, 54, 3, 6, 4, 1, 1, 5]
[5, 54, 3, 6, 4, 1, 1, 64]
[54, 6, 3, 5, 4, 1, 1, 64]
==================

==================
[54, 6, 3, 5, 4, 1, 1, 64]
[1, 6, 3, 5, 4, 1, 54, 64]
[6, 5, 3, 1, 4, 1, 54, 64]
==================
... ...
==================
[1, 1, 3, 4, 5, 6, 54, 64]
[1, 1, 3, 4, 5, 6, 54, 64]
[1, 1, 3, 4, 5, 6, 54, 64]
==================

[1, 1, 3, 4, 5, 6, 54, 64]

优先队列

队列是一种顶部和尾部都开放的数据结构，其中的数据遵循先进先出原则。

优先队列是基于队列的一种扩展，特别适合用堆来实现，其有以下属性：

• 位于优先队列中的每个数据都有自己的优先级
• 高优先级的数据先出
• 同等优先级的数据遵循先进先出原则

优先队列的基本结构：

struct item{
	int item;
	int priority;
}

优先队列的应用：

• 所有的队列应用
• CPU调度
• 图算法

一个典型的优先队列需要实现以下几个功能：

1. 获取其中优先级最高/最低的元素
2. 插入元素
3. 移除优先级最高/最低的元素
4. 减少某个元素的值

同时，堆（基于完全二叉树）对于以上操作的时间复杂度为：

1. O(1)
2. O(Logn)
3. O(Logn)
4. O(logn)

下面是一种以最大堆实现优先队列的方式，可以看到其契合度很高

class PriorityQueue(MaxHeap):

    def insert(self, priority):
        """
        @description  :
            Insert an element to the queue
        ---------
        @param  :
            priority: The element's priority
        -------
        @Returns  :
            True if success
        -------
        """
        
        super().insert(priority)
        return True

    def get_highest_priority(self):
        """
        @description  :
            Get the highest priority element
        ---------
        @param  :
            Void
        -------
        @Returns  :
            The highest priority element
        -------
        """
        return self.get_max()

    def delete_highest_priority(self):
        """
        @description  :
            Remove the highest priority element
        ---------
        @param  :
            Void
        -------
        @Returns  :
            True if success
        -------
        """
        self.extract_max()
        return True


if __name__ == "__main__":
    arr = [54, 6, 1, 64, 4, 1, 3, 5]
    print("初始数据：{}".format(arr))
    priority_queue = PriorityQueue(arr)
    print("优先队列：{}".format(priority_queue.arr))
    inserting_value = 77
    priority_queue.insert(inserting_value)
    print("插入值：{}，插入后：{}".format(inserting_value,priority_queue.arr))
    print("获取优先级最高的元素：{}".format(priority_queue.get_highest_priority()))
    priority_queue.delete_highest_priority()
    print("删除优先级最高的元素后：{}".format(priority_queue.arr))

输出：

(base) ~/.../manjaro_workspace/py100 >>> python test15.py                                                                                                                                                                       
初始数据：[54, 6, 1, 64, 4, 1, 3, 5]
优先队列：[64, 54, 3, 6, 4, 1, 1, 5]
插入值：77，插入后：[77, 64, 3, 54, 4, 1, 1, 5, 6]
获取优先级最高的元素：77
删除优先级最高的元素后：[64, 54, 3, 6, 4, 1, 1, 5]

像红黑树、AVL树之类的自平衡二叉查找树也可以以相同的时间复杂度实现上述功能。

1. 不是原生O(1)，但可以通过添加指针指向到优先级最高、最低的元素实现O(1)复杂的查找。
2. O(Logn)
3. O(Logn)
4. 可以实现为O(logn)

堆实现优先队列的优势：

• 堆是基于数组实现的，基于数组的实现拥有更简单的原生数据结构，操作、读取数据更加友好。
• 虽然有相同的时间复杂度，但是BST（二叉搜索树）的时间复杂度的n更高。
• 在构建数据结构时，堆的时间复杂度为n，BST的时间复杂度为nlogn。
• 堆不需要额外的指针
• 堆实现起来更简单
• 特定的堆实现可以实现O(1)级别时间复杂度的插入、删除操作，比如Fibonacci Heap。

相比于BST，堆的劣势：

• BST执行搜索任务的时间复杂度为O(logn)，而堆是O(n)
• BST按顺序输出全部元素的时间复杂度为O(n)，而堆是O(nlogn)
• BST查找最接近或者等于一个值的元素的时间复杂度为O(nlogn)
• BST可以通过扩展的方式使得在查找第K个大/小的元素时的时间复杂度为O(logn)

图算法

优先队列特别适用于图算法，比如Dijkstra’s Shortest Path和Prim’s Minimum Spanning Tree

其他的有效应用

• 在数组中查找第k个大的元素
• 对乱序性不大的数组进行排序
• 合并已经排好序的数组