二、量子状态的表示和单量子比特门

1. 量子状态的表示

---

1.1 使用 Qiskit 初始化量子态

       我们知道，一个量子的状态可以表示为基态的线性叠加，如果我们使用
$$|0⟩=\left[\begin{array}{c}1\\ 0\end{array}\right]|1⟩=\left[\begin{array}{c}0\\ 1\end{array}\right].$$

表示两个基态，那么任意的一个 qubit 的状态可以表示为

$$|\psi ⟩=\alpha |0⟩+\beta |1⟩$$

       对于任意一个状态，测量的过程可以转换为使用内积求得获得指定状态的概率，这个概率可以表示为 $p(|x⟩)=|⟨x|\psi ⟩{|}^2$ 。例如，对于 $|\psi ⟩$ ，获得 $|0⟩$ 态的概率可以表示为 $p(|0⟩)=|⟨0|\psi ⟩{|}^2$ 。

       对于状态 $|1⟩$ 进行测量，我们将会确定的得到 1。但是对于如下的状态：
$$\left[\begin{array}{c}0\\ i\end{array}\right]=i|1⟩$$

如果我们使用测量规则，可以得到如下结果：
$$|⟨x|(i|1⟩){|}^2=|i⟨x|1⟩{|}^2=|⟨x|1⟩{|}^2$$

我们可以发现，$i$ 对于整个测量过程是没有影响的，状态 $i|1⟩$ 和 $|1⟩$ 的测量概率是相等的（ $i$ 表示虚数，在 python 中使用 $j$ 表示虚数 $i$）。因为测量是我们从 qubit 获取信息的唯一方式，所以从某种程度上来说，这两种状态是等价的。

       更普遍的，如果状态参数 $\gamma$ 的模为 1，即 $|\gamma |=1$ ，那么我们称 $\gamma$ 为全局相位 (global phase)，这个参数对 $|0⟩$ 和 $|1⟩$ 的影响是相同的，不会对最后的测量结果有影响。相反，除了全局相位，我们对只影响 $|0⟩$ 或 $|1⟩$ 的相位为相对相位(relative phase)。

       在 Qiskit 中，线路的默认输入状态都是 $|0⟩$ ，但是我们可以使用 QuantumCircuit 的 initialize() 方法，将一个 qubit 转换为我们想要的叠加态。它的基本用法为：

QuantumCircuit.initialize( [ a, b ] , num)

该方法接收两个参数，第一个参数是一个列表，分别表示叠加状态的 $\alpha$ 和 $\beta$，他们要满足归一性，即 $|\alpha {|}^2+|\beta {|}^2=1$ ；第二个参数 num 表示将第几个 qubit 转换为指定的状态。

       我们可以使用 statevector_simulator模拟器执行线路，然后可以从结果中使用 .get_statevector() 获得状态向量。下面的代码展示了使用这种方法获得状态向量。

from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi

qc = QuantumCircuit(1)
initial_state = [1/sqrt(2),1/sqrt(2)]   #指定初始化状态

qc.initialize(initial_state, 0) # 将 qubit 初始化为指定状态
backend = Aer.get_backend('statevector_simulator') #指定 backend 为 statevector_simulator

result = execute(qc,backend).result() #执行线路
out_state = result.get_statevector()  #获取状态向量

print(out_state) 

"""output
[0.70710678+0.j 0.70710678+0.j]
"""

1.2 观察者效应

       每个量子态在经过测量后就会坍缩为基态中的一个，所以在电路中我们对整个线路执行一次测量后，所有的 qubit 都会坍缩为一个基态，对测量后的线路再次执行也只是使用基态在执行线路。下面展示了一个例子，该线路使用先将状态初始化为一个指定状态，然后对状态进行测量。执行该线路，输出测量结果，在运行后再次执行该电路多次，可以发现得到的结果和测量后的结果一直相同，这表示量子态已经坍缩到基态，再次执行也不会改变状态了。

from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi

qc = QuantumCircuit(1)

initial_state = [1/sqrt(3),sqrt(2)/sqrt(3)]    #指定初始状态
qc.initialize(initial_state, 0)                #初始化输入状态


backend = Aer.get_backend('statevector_simulator')   #指定模拟器
result = execute(qc,backend).result()                #执行线路，获取结果
out_state = result.get_statevector()                 #得到状态向量
counts = result.get_counts()                         #获取输出结果的占比

print('out_state:',out_state)                        #输出向量
print('counts:',counts)                              #输出结果的占比

"""output
out_state: [0.57735027+0.j 0.81649658+0.j]
counts: {'0': 0.333333333333333, '1': 0.666666666666667}
"""

qc.measure_all() #测量线路中的所有 qubit

#第二次执行线路
result = execute(qc,backend).result()
out_state = result.get_statevector()
counts = result.get_counts()

print('out_state:',out_state)                       #输出向量
print('counts:',counts)                             #输出结果的占比

"""output 输出的结果
out_state: [1.+0.j 0.+0.j]
counts: {'0': 1}
"""

#第三次次执行线路
result = execute(qc,backend).result()
out_state = result.get_statevector()
counts = result.get_counts()

print('out_state:',out_state)                      #输出向量
print('counts:',counts)                            #输出结果的占比

"""output 输出的结果
out_state: [1.+0.j 0.+0.j]
counts: {'0': 1}
"""
qc.draw()

       我们可以发现，在第一次执行测量之后，后面的结果其实就已经固定了，因为 qubit 已经坍缩到了某个基态，因此我们如果想要得到 qubit 的状态，应该将测量放在线路的最后，否则可能回对之后的运行造成影响。这里我们也可以看出，对于含有 global phase 的量子态，我们进行测量后，global phase 仍然存在，在真正的量子计算机上，我们永远无法测量 global phase 。

       量子的状态可以写成上面的叠加状态，但是在真正的量子计算机上我们只能得到确定的 qubit 0 或 qubit 1，也就是得到一串确定的比特流，并不能得到中间的量子态，量子态的概率性也不能体现出来，为了模拟得到这个量子态，Qiskit 提供了两种不同的模拟器，qasm_simulator 和真实计算机中的结果一样，只能的到确定的 bit 0 或 1 ，statevector_simulator 能够让我们在测量前获得叠加的量子状态。

1.3 布洛赫球

一个量子态可以表示为
$$|q⟩=\alpha |0⟩+\beta |1⟩，\alpha ,\beta \in \mathbb{C}$$

通过后面的条件我们可以知道，量子态的系数都是复数，在上面我们也知道，对于有 global phase 的状态，我们并不能对他们进行区分，那么我们有没有更好的方法表示一个量子的状态呢？之所以我们不能区分有 global phase 的状态，是因为 $\alpha$ 和 $\beta$ 可以取复数，我们可以将他们的取值限制为实数，然后为他们增加一项，从而让我们知道他们的 relative phase，如下定义
$$|q⟩=\alpha |0⟩+e^{i\varphi }\beta |1⟩，\alpha ,\beta ,\varphi \in \mathbb{R}$$

因为量子态必须是归一的，即
$$\sqrt{{\alpha }^2+{\beta }^2}=1$$

所以我们可以使用三角函数表示它们，即
$$\sqrt{{\sin }^{2}x+{\cos }^{2}x}=1$$

为了使用同一个变量 $\theta$ 表示 $\alpha$ 和 $\beta$，我们将 $\alpha$ 和 $\beta$ 表示如下：
$$\alpha =\cos \frac{\theta }{2},\beta =\sin \frac{\theta }{2}$$

因此，我们可以使用两个变量 $\varphi$ 和 $\theta$ 表示量子态：
$$|q⟩=\cos \frac{\theta }{2}|0⟩+e^{i\varphi }\sin \frac{\theta }{2}|1⟩，\theta ,\varphi \in \mathbb{R}$$

1.4 可视化量子比特

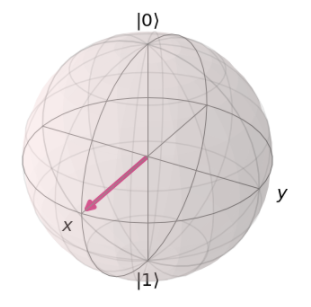
       如果我们将 $\varphi$ 和 $\theta$ 看作球坐标系中的参数（其中 $r=1$，因为比特状态的模长为 1 ），那么我们可以在一个球面中画出任意的量子态，我们称为 布洛赫球(Bloch sphere)。Qiskit 中提供了将量子态转换为在布洛赫球中表示的方法，使用 qiskit.visualization 中的 plot_bloch_vector 即可实现。下面展示了 plot_bloch_vector 的用法。

from qiskit.visualization import plot_bloch_vector

coords = [1,0,0]                       #coords[<r>,<theta>,<phi>] 
plot_bloch_vector(coords)              #theta 是和z轴的夹角，phi 是和 x轴的夹角

2. 单量子比特门

       量子线路的一个重要特点是，对量子的操作（量子门）是可逆的，这些可逆的门可以表示为矩阵，也可以表示为围绕布洛赫球的旋转。

2.1 泡利门 (The Pauli Gates)

2.1.1 The X-Gate

X-gate 可以表示为 Pauli-X 矩阵：
$$X=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]=|0⟩⟨1|+|1⟩⟨0|$$

X-gate 的作用是执行 比特翻转，它可以将 $|0⟩$ 转换为 $|1⟩$ ，将 $|1⟩$ 转换为 $|1⟩$ 。在 Qiskit 中，我们使用 x 操作实现 X-gate 。下面展示了使用 X-gate 对输入 qubit 进行操作，从结果可以看出，X-gate 将 $|0⟩$ 态转换为了 $|1⟩$。

       我们可以使用 qiskit.visualization.plot_bloch_multivector 来将状态向量在布洛赫球中表示出来。

from qiskit import QuantumCircuit, execute, Aer
from math import pi
from qiskit.visualization import plot_bloch_multivector

qc = QuantumCircuit(2)
qc.x(1)
qc.draw()

backend = Aer.get_backend('statevector_simulator')     #设置模拟器
out = execute(qc,backend).result().get_statevector()   #执行线路

plot_bloch_multivector(out)     #使用布洛赫球表示状态向量

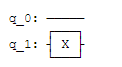
2.1.2 The Y-gate & Z -gate

Y-gate 为 Pauli-Y 矩阵，它表示如下，Y-gate 在布洛赫球面表达下将使目标量子位绕 y 轴旋转 180 度。
$$Y=\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right]=-i|0⟩⟨1|+i|1⟩⟨0|$$

Z-gate 为 Pauli-Z 矩阵，表示如下，它是将 $|1⟩$ 转换为 $-|1⟩$。
$$Z=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]=|0⟩⟨0|-|1⟩⟨1|$$

       在 Qiskit 中，使用 y 和 z 分别表示 Y-gate 和 Z-gate，下面展示了他们的作用方式和结果。

from qiskit import QuantumCircuit, execute, Aer
from math import pi
from qiskit.visualization import plot_bloch_multivector

qc = QuantumCircuit(3)     #创建有三个 qubit 的线路
qc.y(1)                    #对第二个 qubit 使用 Y-gate
qc.z(2)					   #对第三个 qubit 使用 Z-gate
qc.draw()

backend = Aer.get_backend('statevector_simulator')
out = execute(qc,backend).result().get_statevector()
plot_bloch_multivector(out)    #使用布洛赫球表示状态向量

       通过计算我们可以发现 $|0⟩$ 和 $|1⟩$ 其实是 Z-gate 的特征向量，它们对应于 Z 轴的上下两个方向，我们称为 Z-basis；而 $|+⟩$ 和 $|-⟩$ 是 X-gate 的特征向量，对应于 X 轴前后两个方向，称为 X-basis 。Y-gate 的特征向量也可以组合成为一组基态，他们对应 Y 轴的左右两个方向，所以其实我们有无穷多个基态，只要保持他们是正交的向量即可。

2.2 The Hadamard Gates

The Hadamard Gates（H-gate），是一个基本的量子门，它可以让我们创建一个叠加态。泡利门只能让我们实现状态 $|0⟩$ 和 $|1⟩$ 之间的转换，但是我们并不能得到叠加态。H-gate 可以用矩阵表示为：
$$H=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$

H-gate 作用在 $|0⟩$ 和 $|1⟩$ 可以表示如下：
$$H|0⟩=|+⟩$$

$$H|1⟩=|-⟩$$

H-gate 可以看作是将状态绕 x轴 和 z轴 中间的 $z=x$ 这条线进行旋转，也可以看做是 X-basis 和 Z-basis 之间的转换。下面是使用 Qiskit 应用 H-gate 的一个例子。

from qiskit import QuantumCircuit, execute, Aer
from math import pi
from qiskit.visualization import plot_bloch_multivector


qc = QuantumCircuit(2)
qc.h(1)      #在第二个 qubit 上使用 H-gate
qc.draw()


backend = Aer.get_backend('statevector_simulator')
out = execute(qc,backend).result().get_statevector()
plot_bloch_multivector(out)

2.3 使用不同基态进行测量

       在对 qubit 测量时我们可以选择不同的基态，在不同的基态测量可能会得到不同的结果，例如，我们在 X-basis 下测量得到各个基态的概率就可以表示为：
$$p(|+⟩)=|⟨+|q⟩{|}^2,p(|-⟩)=|⟨-|q⟩{|}^2$$

       经过测量，我们可以确定的得到两个基态中的一个，但是 Qiskit 中仅仅支持在 Z-basis 下测量，即得到 $|0⟩$ 或 $|1⟩$ ，如果我们想要在其他基态下测量，需要使用 H-gate 构建。下面创建了一个基于 X-basis 的测量方式，在两个 H-gate 之间加入一个基于 Z-basis 的测量，就可以实现在 X-basis 下的测量。

from qiskit import QuantumCircuit, execute, Aer
from math import pi
from qiskit.visualization import plot_bloch_multivector

def x_measurement(qc,qubit,cbit):
    #将 qubit 的测量结果保存到 cbit
    qc.h(qubit)
    qc.measure(qubit, cbit)
    qc.h(qubit)
    return qc

initial_state = [0,1]  #初始化状态为 |1>

qc = QuantumCircuit(1,1)
qc.initialize(initial_state, 0)
x_measurement(qc, 0, 0)   #使用 X-basis 测量
qc.draw()

backend = Aer.get_backend('statevector_simulator') 
out_state = execute(qc,backend).result().get_statevector() 
plot_bloch_multivector(out_state) 

       我们将状态初始化为 $|1⟩$ ，如果在 Z-basis 下测量，我们只能得到 $|1⟩$ ，但是在 X-basis 下测量，我们可以随机的得到 $|+⟩$ 或 $|-⟩$ 中的任意一个。

       在 Z-basis 上测量一个状态，将消除在 X-basis 上测量特定状态的所有确定性，反之亦然。无论我们的量子系统处于什么状态，总有一种测量，在这种测量下，得到的结果是确定的。

2.4 The R${}_{\mathbf{\varphi }}$-gate

       R${}_{\varphi }$-gate 是一个带有参数的门，在使用是我们需要给定一个数字 $\varphi$ 。它表示将布洛赫向量围绕 Z轴 方向旋转 $\varphi$ 角度，所以有时候也称为 R${}_{\mathrm{z}}$-gate 。矩阵表示为：
$$R_{\varphi }=\left[\begin{array}{cc}1& 0\\ 0& e^{i\varphi }\end{array}\right]$$

其中 $\varphi$ 是一个实数。

在 Qiskit 中使用 rz(phi, qubit) 表示 R${}_{\varphi }$-gate 。

from qiskit import QuantumCircuit, execute, Aer
from math import pi
from qiskit.visualization import plot_bloch_multivector

qc = QuantumCircuit(2)  #创建有两个 qubit 的线路

qc.h(0)     #将两个 qubit 调整到 x 轴以观察效果
qc.h(1)

qc.rz(pi/2, 1)  #将 qubit 1 绕 z 轴旋转 pi/2 角度
qc.draw()

backend = Aer.get_backend('statevector_simulator') 
out_state = execute(qc,backend).result().get_statevector() 
plot_bloch_multivector(out_state) 

2.5 The I-gate, S-gate and T-gate

2.5.1 The I-gate

I-gate 表示等价门，也就是单位向量，I-gate 门作用在线路上不会对 qubit 有任何影响，可以用单位矩阵表示为：
$$I=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

2.5.2 The S-gates

S-gate 是 $\varphi =\frac{\pi }{2}$ 时的 R${}_{\varphi }$-gate，它表示绕 Z轴 旋转 $90^{°}$ 。S${}^{†}$-gate 是在 $\varphi =-\frac{\pi }{2}$ 时的 R${}_{\varphi }$-gate 门。它们可以用矩阵表示为：
$$S=\left[\begin{array}{cc}1& 0\\ 0& e^{\frac{i\pi }{2}}\end{array}\right],S^{†}=\left[\begin{array}{cc}1& 0\\ 0& e^{-\frac{i\pi }{2}}\end{array}\right]$$

S-gate 和 S${}^{†}$-gate 也分别被称为 $\sqrt{}Z$-gate 和 $\sqrt{}{Z}^{†}$-gate ，因为两个连续的 S-gate 等价于使用一次 Z-gate ，即：
$$SS|q⟩=Z|q⟩$$

在 Qiskit 中，我们使用 s() 和 sdg() 分别表示 S-gate 和 S${}^{†}$-gate 。

from qiskit import QuantumCircuit, execute, Aer
from math import pi
from qiskit.visualization import plot_bloch_multivector

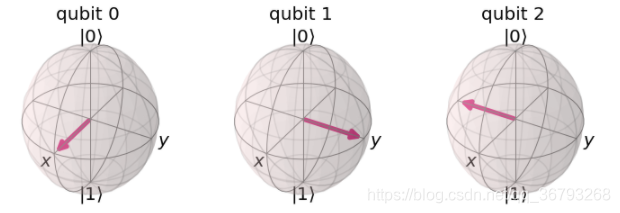
qc = QuantumCircuit(3)

qc.h(0)
qc.h(1)
qc.h(2)


qc.s(1)  #对 qubit 1 施加 S-gate
qc.sdg(2) 
qc.draw()

backend = Aer.get_backend('statevector_simulator') 
out_state = execute(qc,backend).result().get_statevector() 
plot_bloch_multivector(out_state) 

2.5.3 The T-gate

T-gates 是在 $\varphi =\pi /4$ 时的 R${}_{\varphi }$-gate ，分别表示为：
$$T=\left[\begin{array}{cc}1& 0\\ 0& e^{\frac{i\pi }{4}}\end{array}\right],T^{†}=\left[\begin{array}{cc}1& 0\\ 0& e^{-\frac{i\pi }{4}}\end{array}\right]$$

类似于 S-gate ，T-gate 也可以表示为 $\sqrt{}Z$-gate 。

在 Qiskit 中使用 t() 和 tdg() 表示。

from qiskit import QuantumCircuit, execute, Aer
from math import pi
from qiskit.visualization import plot_bloch_multivector

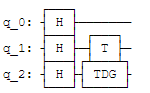
qc = QuantumCircuit(3)

qc.h(0)
qc.h(1)
qc.h(2)


qc.t(1)  #在 qubit 1 施加 T-gate
qc.tdg(2)

qc.draw()


backend = Aer.get_backend('statevector_simulator') 
out_state = execute(qc,backend).result().get_statevector() 
plot_bloch_multivector(out_state) 

2.6 General U-gates

       从上面我们可以看出，I, Z, S & T-gates 都是 R${}_{\varphi }$-gate 的特殊情况。其实 U${}_3$-gate 是所有单量子比特的通用形式，它是一个参数化的门，可以表示为：
$$U_3(\theta ,\varphi ,\lambda )=\left[\begin{array}{cc}\cos (\theta /2)& -e^{i\lambda }\sin (\theta /2)\\ e^{i\varphi }\sin (\theta /2)& e^{i\lambda +i\varphi }\cos (\theta /2)\end{array}\right]$$

       上面所展示的所有的门都可以通过固定 $U_3(\theta ,\varphi ,\lambda )$ 中的参数确定。

       Qiskit 提供了 U${}_2$-gate 和 U${}_3$-gate ，它们分别是 $\theta =\frac{\pi }{2}$，和 $\theta =\varphi =0$ 时的 U${}_3$ 门。其实 U${}_1$-gate 就等价于 R${}_{\varphi }$-gate 。
$$\begin{array}{rlr}{U}_3(\frac{\pi }{2},\varphi ,\lambda )=U_2=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& -e^{i\lambda }\\ e^{i\varphi }& e^{i\lambda +i\varphi }\end{array}\right]& & U_3(0,0,\lambda )=U_1=\left[\begin{array}{cc}1& 0\\ 0& e^{i\lambda }\end{array}\right]\end{array}$$

       在使用真正的 IBM 量子硬件运行线路时，所有的单量子比特操作都先被编译为 $U_1$，$U_2$ 和 $U_3$ ,因为他们又被称为物理门。