摄动:天体受到另一个及以上的天体的引力而产生的复杂运动
摄动理论
微分方程的精确解为 ,近似解
,近似解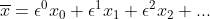
以微扰 的简并度来分辨:无简并或有简并。有简并的摄动,又称为奇异摄动(singular perturbation),比较难解,必须用到更进阶的理论。
的简并度来分辨:无简并或有简并。有简并的摄动,又称为奇异摄动(singular perturbation),比较难解,必须用到更进阶的理论。
补充1
Berman问题:长宽远大于平板间距的两个平板,两个平板有孔通入流体![]()
该问题对应的方程为二维的连续性方程与动量方程,重点在边界条件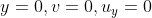 两板中间,法向速度为0,水平速度达到最大值
两板中间,法向速度为0,水平速度达到最大值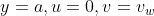 上板处,水平速度为0,法向速度为流体入口速度
上板处,水平速度为0,法向速度为流体入口速度
补充2
一些问题的数学建模为带小参数的PDE,如润滑理论的雷诺方程。
Boussinesq范式方程,用来模拟浅水海岸的水波运动(NS方程求解困难)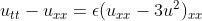
初始条件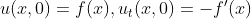
该方程带有小参数 ,可以设近似解
,可以设近似解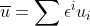

带入近似解方程转化为两个方程。第一个为齐次波动方程,求解出 ,将
,将 带入第二个方程,则第二个方程为非齐次波动方程,求解
带入第二个方程,则第二个方程为非齐次波动方程,求解 。齐次与非齐次波动方程都有再将边界条件带入,得到最终近似解
。齐次与非齐次波动方程都有再将边界条件带入,得到最终近似解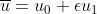 。
。
齐次波动方程的行波解:自变量的线性组合做变量代换来进行求解,u的自变量为x与t,线性组合为x+λt,解为
补充3
问题的边界条件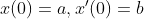
近似解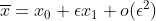
那么 ,
,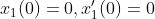
后续了解:
通解、特解
完备解
奇异解:指无法由通解中求出但仍能符合微分方程式的解,奇异解只会在非线性方程式中才会出现
渐进解








 本文探讨了天体摄动理论及其在流体力学中的应用,包括Berman问题中平板间流体流动的建模,以及润滑理论中雷诺方程的处理。通过Boussinesq范式方程,分析了浅水海岸水波运动的近似解法。文章还提到了奇异摄动和非线性方程的奇异解,以及在解决这类问题时采用的渐进解方法。
本文探讨了天体摄动理论及其在流体力学中的应用,包括Berman问题中平板间流体流动的建模,以及润滑理论中雷诺方程的处理。通过Boussinesq范式方程,分析了浅水海岸水波运动的近似解法。文章还提到了奇异摄动和非线性方程的奇异解,以及在解决这类问题时采用的渐进解方法。
















 562
562

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








