【通俗理解】Jensen不等式则像是一个“期望计算器”，它告诉我们当这个函数作用于一个随机变量的期望时，会得到一个不小于该函数在随机变量期望值处的值的结果

【通俗理解】凸函数与Jensen不等式在期望计算中的应用

关键词提炼

#凸函数 #Jensen不等式 #期望计算 #下界估计 #概率论 #优化问题

第一节：凸函数与Jensen不等式的类比与核心概念【尽可能通俗】

凸函数就像是一个“碗状”的函数，它的形状保证了在任何两点之间的线段都会位于函数图像的上方。而Jensen不等式则像是一个“期望计算器”，它告诉我们当这个函数作用于一个随机变量的期望时，会得到一个不小于该函数在随机变量期望值处的值的结果。这就像是我们用一个“凸透镜”去看这个期望，使得我们看到的结果总是偏大一些。

第二节：凸函数与Jensen不等式的核心概念与应用

2.1 核心概念

核心概念	定义	比喻或解释
凸函数	对于任意两点x, y和参数λ∈[0,1]，有f(λx+(1-λ)y) ≤ λf(x)+(1-λ)f(y)。	像是一个“碗状”的函数，线段总在函数图像上方。
Jensen不等式	对于凸函数f(x)和随机变量X，有E[f(X)] ≥ f(E[X])。	像是用“凸透镜”看期望，结果总是偏大。

2.2 优势与劣势

方面	描述
优势	提供了期望计算的下界估计，对于优化问题特别有用。
劣势	仅限于凸函数或凹函数，对于其他类型的函数可能无法应用。

2.3 与期望计算的类比

Jensen不等式在期望计算中扮演着“下界估计器”的角色，它能够帮助我们找到一个复杂期望计算的最小可能值，就像是在拍卖会上，我们提前知道了一个物品的最低价格，从而能够更明智地进行竞价。

第三节：公式探索与推演运算

3.1 凸函数的基本性质

凸函数的基本性质可以表示为：

$$f(\lambda x+(1-\lambda )y)\le \lambda f(x)+(1-\lambda )f(y)$$

其中，λ∈[0,1]，x和y是任意两点。

3.2 Jensen不等式的基本形式

Jensen不等式的基本形式为：

$$E[f(X)]\ge f(E[X])$$

其中，f(x)是一个凸函数，X是一个随机变量，E表示期望。

3.3 公式推导与实例

假设我们有一个凸函数f(x)和一个随机变量X，其期望为E[X]。根据凸函数的性质，对于任意x和y，都有：

$$f(\lambda x+(1-\lambda )y)\le \lambda f(x)+(1-\lambda )f(y)$$

当我们将这个性质应用到随机变量X上时，可以想象X的取值就像是x和y的无数个可能组合。因此，我们可以对每一个可能的取值应用凸函数的性质，并将它们加权平均起来，得到：

$$f(E[X])=f\left(\int xp(x)dx\right)\le \int f(x)p(x)dx=E[f(X)]$$

其中，p(x)是X的概率密度函数。

3.4 具体实例

假设我们有一个凸函数f(x) = x^2，以及一个随机变量X，其期望E[X] = 0。我们可以计算E[f(X)]和f(E[X])来验证Jensen不等式：

$$E[f(X)]=E[X^2]=\text{Var}(X)+(E[X]{)}^2=\text{Var}(X)$$

$$f(E[X])=f(0)=0$$

由于方差Var(X)总是非负的，因此我们有：

$$E[f(X)]\ge f(E[X])$$

这验证了Jensen不等式。

第四节：相似公式比对

公式/不等式	共同点	不同点
Markov不等式	都提供了期望或概率的界。	Markov不等式提供了随机变量取值大于某个值的概率的上界，而Jensen不等式提供了期望值的下界。
Chebyshev不等式	都与期望和方差有关。	Chebyshev不等式提供了随机变量取值偏离期望的概率的上界，而Jensen不等式关注期望值的计算。

第五节：核心代码与可视化

下面是一个使用Python和matplotlib库来可视化凸函数和Jensen不等式的简单示例。请注意，这只是一个示意性的代码，用于帮助理解概念。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 定义凸函数f(x)
def f(x):
    return x**2  # 示例凸函数

# 生成样本数据
x = np.linspace(-5, 5, 1000)
y = f(x)

# 计算期望E[X]和E[f(X)]
E_X = 0  # 假设X的期望为0
E_f_X = np.mean(f(x))  # 计算E[f(X)]
f_E_X = f(E_X)  # 计算f(E[X])

# 可视化结果
sns.set_theme(style="whitegrid")
plt.plot(x, y, label='Convex Function f(x)')
plt.axhline(y=E_f_X, color='green', linestyle='-.', label=f'E[f(X)]={E_f_X:.2f}')
plt.axhline(y=f_E_X, color='purple', linestyle=':', label=f'f(E[X])={f_E_X:.2f}')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Convex Function and Jensen Inequality')
plt.legend()

# 添加重点区域的标注
plt.annotate('E[f(X)]', xy=(0, E_f_X), xytext=(0.7, 0.9), textcoords='axes fraction',
             bbox=dict(boxstyle='round,pad=0.5', fc='green', alpha=0.5),
             arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0'))
plt.annotate('f(E[X])', xy=(0, f_E_X), xytext=(0.7, 0.8), textcoords='axes fraction',
             bbox=dict(boxstyle='round,pad=0.5', fc='purple', alpha=0.5),
             arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0'))

plt.show()

# 打印详细的输出信息
print(f"E[f(X)] (Expected value of f(X)): {E_f_X:.2f}")
print(f"f(E[X]) (Value of f at the expected value of X): {f_E_X:.2f}")
print(f"According to Jensen's Inequality, E[f(X)] should be greater than or equal to f(E[X]).")

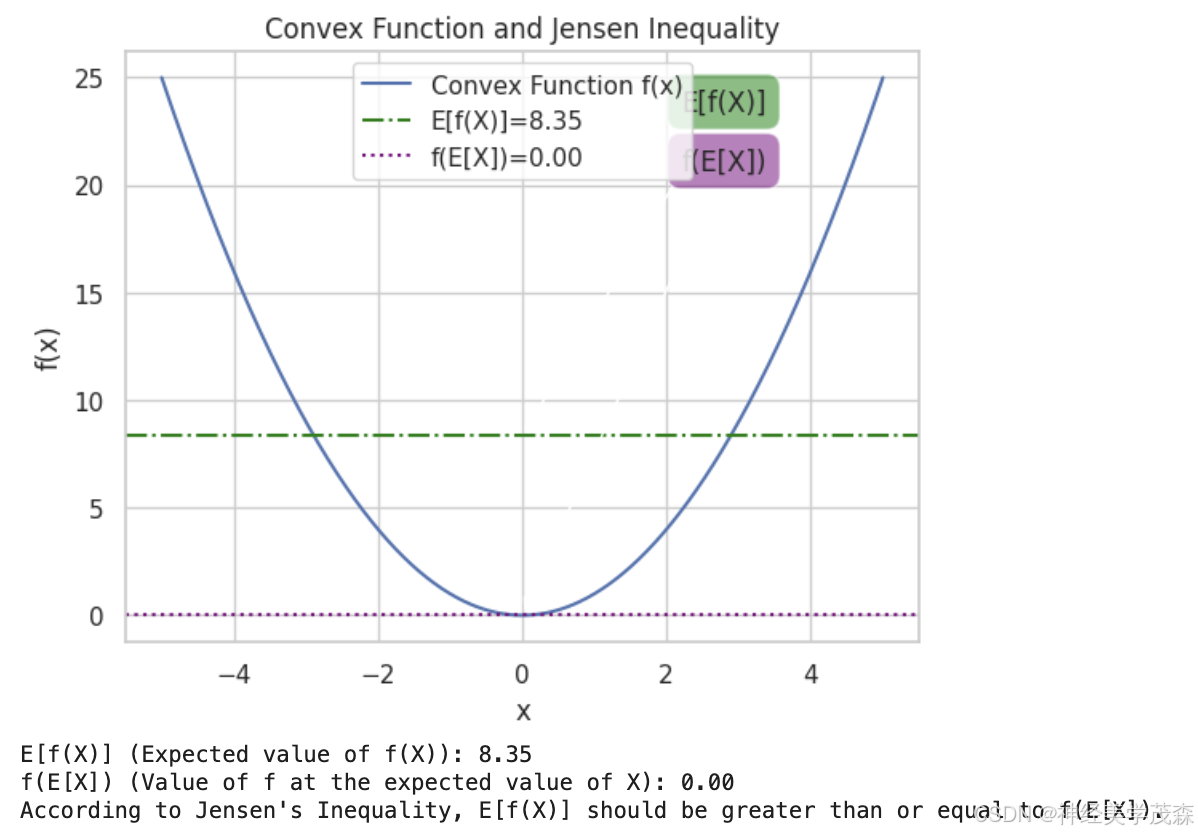
输出内容	描述
凸函数f(x)的图示	显示了凸函数的形状。
E[f(X)]和f(E[X])的标注	在图表上标注了E[f(X)]和f(E[X])的值。
详细的输出信息（打印到控制台）	提供了关于E[f(X)]和f(E[X])的详细解释。

“凸函数就像是一个‘碗状’的函数，它的形状保证了Jensen不等式能够成立。而Jensen不等式则像是一个‘期望的下界估计器’，它告诉我们当这个函数作用于一个随机变量的期望时，结果总是偏大。”