设备健康度评价实践--煤磨机

煤磨健康度评价说明
源码实现：http://t.csdnimg.cn/ysDHp

1. 煤磨健康度评价模型

   在以可靠性为中心的维护理论中，一般用健康度量化描述设备的健康状态，它是指在规定的时间和条件下，设备持续完成预定功能的能力大小，是表达设备或零件状态好坏的定量指标。

煤磨的健康状态评价原则是要求能够真实地反映磨机的健康状态，结合磨机故障特征及状态监测参数的分析，选取了易于测量、并能较好的反映磨机状态的参数，建立磨机状态层次评价模型。该模型从磨机的工艺状态和系统状态两个方面出发，分别评价磨机的健康状态。评价模型如下图所示：

1. 参数健康度和权重计算

   参数健康度和权重，是煤磨健康度计算的基础，本项目是以python程序实现，运行在平台算法在线服务上面，如下图所示

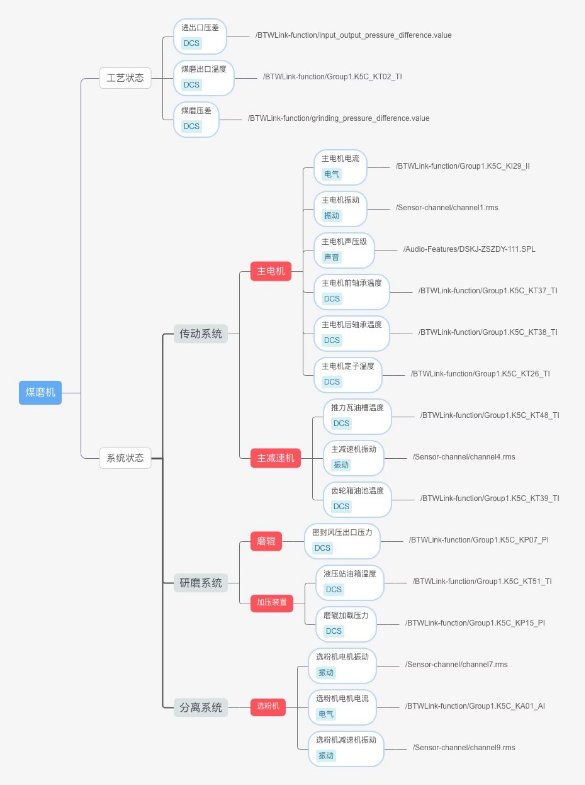
其计算逻辑说明如下：

1. 参数含义

   参数是健康度评价体系中的最末一级，以选粉机参数为例，包括选粉机电机振动、选粉机电机电流、选粉机减速机振动三个参数。

影响立磨运行状况的因素比较繁杂，为了能够准确全面反映磨机的运行状态，选取评价参数时遵循以下原则：

（1）针对磨机的每个关键部件，选取指标数量要适当，既要保证全面的反映评价对象的特性特征，又不能数目太多，主要以对评价过程起重要作用的程度为原则。

（2）评价磨机单个部件的几个指标都要单独刻画评价对象的一个特征，不重叠、不关联。

（3）每个评价指标应具有代表性、可比性，并且符合评价对象的客观规律，还要保证易于操作、可测量。

1. 参数健康度计算

   参数健康度计算公式，与参数类型（正向参数、负向参数、中间型参数）有关。

• 对于正向参数，即数值越大性能越优、健康度越高的参数，其健康度计算公式如下：

• 对于负向参数，即数值越小性能越优、健康度越高的参数，其健康度计算公式如下：

• 对于中间型参数，即数值越接近标准值性能越优、健康度越高的参数，其健康度计算公式如下：

其中， x ， x0 分别为单个指标的测量值和标准值，[xmin , xmax ]为该指标的阈值范围； x’为指标的量化值，取值范围为［0，1］；当指标测量值超过阈值范围时， x’ =0；当指标测量值与标准值重合时， x’ =1，表示性能最佳，状态最好。

有了参数的健康度结果后，为了计算各部件的健康度，还需要每个参数的权重，权重计算包括层次权重、熵权、组合权重、变权重计算4个计算步骤。

1. 层次权重计算

   各参数层次权重主要依赖人工经验（但并不是直接指定参数的权重），根据参数的相对重要性进行主观判断并构成判断矩阵，由此计算各参数权重。具体计算步骤如下：

1. 引入函数 f(x，y)，用来表示x与y对评价对象的重要性标度，约定 f(x，y)=1/f(y, x)。重要性一般是用 1~9 标度，如下所示：

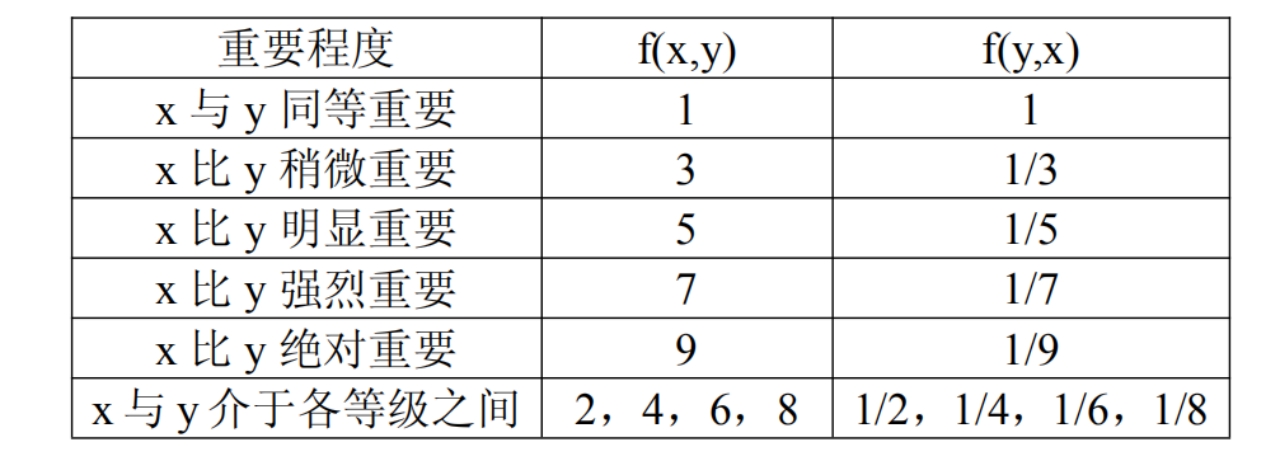
1. 判断矩阵。设 X= (x1，x2，…，xn)是全部因素的集，可根据专家经验按上表的标度，对全部因素作两两之间的比较，构造判断矩阵，其中)且 cii=1。
2. 权重。根据判断矩阵 C，计算它的最大特征根lmax ，即求满足如下条件的lmax：

求出矩阵 C 关于lmax 的特征向量，经过归一化处理后的各元素即为各参数的权重，即：

1. 熵权重计算

   熵用来衡量事物出现的不确定性。一个对象的信息熵 Ej 越小，表明其性能变化程度越大，透露出的信息量越大，则其重要性也越大，权重就应越大；反之，则其权重也应越小。

若某评价参数 xj 有 m 个数据，其信息熵为：

其中， pij为参数 xj 的归一化值，第 j 个参数的熵权wj 为：

1. 组合权重计算

   综合采用层次权重和熵权重，形成的组合权重如下所示：

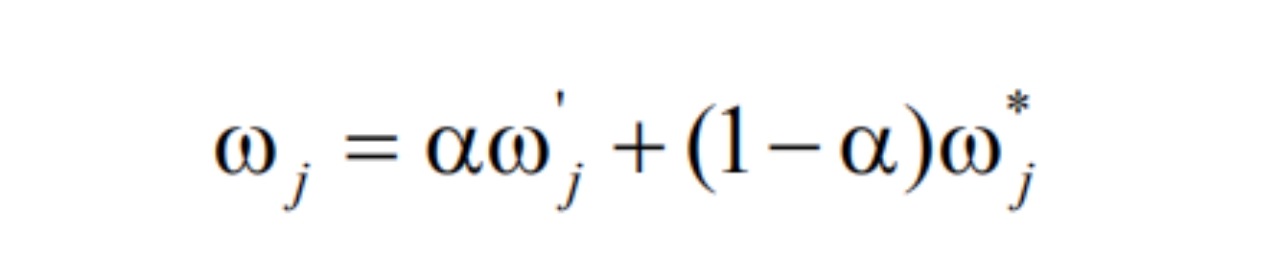
其中，wj为组合权重，w’j为为层次分析法所得权重， 为熵权重。

，GAHP为层次分析法中各分量差异系数：

其中，n 为指标个数， pi为层次分析法中权重系数从小到大的重新排序。

1. 变权重计算

   上述组合赋权法求得权重，已经能够体现各参数的相对重要性，但仍然不能及时跟踪参数的波动。例如，当磨机关键部件的某个参数数值严重偏离标准值时，往往可以说明该部件的健康状态已经出了较大问题，如果利用常权重来进行评估，当其他指标无变化或变化不大时，就可能会掩盖该指标的消极作用，造成评价结果显示正常状态，就会丧失对磨机状态的跟踪能力。而变权重理恰好可以突出各参数的偏离程度，反映参数状态的均衡性。因此，这里使用变权理论来修正组合权重，让参数权重随其状态及时变化，弥补异常参数的“短板效应”。为此，引入变权公式为：

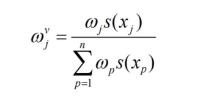
上述式中，s(x) 为均衡函数。

由于指数型函数具有结构简单、反应灵敏、可扩展性强等优点，以此建立“惩罚型”状态变权向量，对于偏离正常值的指标，根据指标超限的偏离程度调整权重大小；指标偏离越严重，其状态变权向量越大，相应的变权权重也就越大，则均衡函数为：

式中， xj 为参数监测数值， l j 为参数的惩罚阈值（即参数标准值）；ε为惩罚水平（ε>0），当ε越大时，惩罚效果越明显，即指标微小变动就会造成评价结果波动；xmax、xmin 分别为第 j 项指标的阈值区间上、下限。

1. 部件、子系统、整机健康度和权重计算

   1. 健康度计算

      部件、子系统、整机的健康度计算，都是作为计算指标，基于平台指标工具实现，以选粉机健康度计算为例，如下图所示：

平台指标工具，支持以鱼骨图的方式，直观展现计算指标的来龙去脉，并能查看指标实时值，进行重计算等操作，如下图所示：

1. 权重计算

   部件、子系统的权重均采用层次权重进行计算，算法运行在算法在线服务上面，具体逻辑可参见“1.2.3层次权重计算”。

2. 备注

   健康度评分计算健康状态

算法demo源码：https://download.csdn.net/download/qq_37279279/89567442