层次分析法（AHP）—以b站up主评价问题为例

大家好，我是北海。

本期课程讲解层次分析法的基本概念，核心思想就是如何构造判断矩阵并求出权重。课程视频已在b站更新：

https://www.bilibili.com/video/BV1Ja411B7HR?p=3&share_source=copy_web

例题

对以下几位b站up主进行综合评价，评选出综合得分第一名：老番茄、老师好我叫何同学、木鱼水心、凉风Kaze、罗翔说刑法。

对于评价类问题，可以采用层次分析法求解。层次分析法结构如下图所示：

模型包括三大部分：目标层、准则层和方案层。

• 目标层：对5位up主进行综合评价，评选出第一名

• 准则层：以4项指标作为评价准则，指标的数据可从up主个人主页找到

• 方案层：每一位up主都有可能是第一，所以有5个方案

如何根据4项指标对5位up主进行综合评价？

简单粗暴法：粉丝数+最高播放数+获赞数+稿件数，数值最大的就是第一。类似于平时考试，考了四门课，总分最高的就是年级第一。

但指标的数量级不同：播放数几千万，稿件数一般几百，简单相加，加了个寂寞。

因此需要先对每一行的数组[a, b, c, d]归一化处理得到[a/(a+b+c+d), b/(a+b+c+d), c/(a+b+c+d), d/(a+b+c+d) ]

利用归一化后的数据，四项指标相加求出总分，可见分数最高的是老番茄。

但这样做，忽略了一个问题：现实中指标对于评价的重要性不同。一般来说，粉丝数比稿件数更能体现up主的优秀。

因此需要指标数值乘以权重再相加，以区分重要性。

例如假设 综合评分 = 0.4粉丝数+0.2播放数+0.3获赞数+0.1稿件数，这样粉丝数的重要性就明显高于稿件数了。

注意，权重是人为主观设定的，这也是层次分析法的缺点。

因此可能出现极端情况：主观认为稿件数权重是1，其他指标设为0，会带来荒谬的结论。

例如下面两位up主，如果只看稿件数的话，右边的up主的得分会高于左边的up主，这显然是不合理的。

 因此当前问题转化为：如何较为科学地设定权重？

判断矩阵

如何较为科学地设定权重？

基本思路是：通过对指标的重要性进行两两比较，构造判断矩阵，从而求出权重。

判断矩阵中元素𝑎𝑖𝑗的意义是，第𝑖个指标相对第𝑗个指标的重要程度。

粉丝数和稿件数相比，根据文献或个人主观认为，粉丝数比稿件数明显重要，则设置𝑎14为5

反过来，稿件数相比粉丝数的重要性那就是1/5， 𝑎41为1/5。

如此求得矩阵中的每个元素值，得到整个判断矩阵：

 但是仔细观察该矩阵，会发现存在矛盾：

• 设粉丝数为A，最高播放数为B，获赞数为C，稿件数为D
• 𝑎23=1/2意味着在重要性上，B<C； 𝑎24=2意味着B>D；因此D<B<C
• 而𝑎34=1/3意味着C<D，与上一条矛盾！

出现前后不一致的矛盾，是因为每一次两两比较的过程中暂时忽略了其他因素，导致最后的结果可能出现矛盾。

在数学上可证明，理想情况下：满足𝑎𝑖𝑗=𝑎𝑖𝑘∗𝑎𝑘𝑗且矩阵各行（列）成倍数关系的矩阵，称为一致矩阵，不会出现矛盾的情况（证明略）。

但因为权重的设定带有主观性，难以得到严格的一致矩阵

因此退一步，我们构造的判断矩阵只需和一致矩阵的“差异”不大即可，求出并检验“差异”的过程称为一致性检验。

一致性检验

计算一致性比例CR

其中

为矩阵的最大特征值，n为评价标准数，即矩阵行（列）数。

𝑅𝐼为平均随机一致性指标，通过查表可得到不同的𝑛对应的𝑅𝐼。一般n不会超过10，如果评价标准过多，可以考虑构建多级评价。

• 如果一致性比例𝐶𝑅=0 ，说明判断矩阵是一致矩阵，不会出现任何矛盾的情况（证明略）
• 如果一致性比例𝐶𝑅<0.1,可以认为判断矩阵一致矩阵的“差异”不大，通过一致性检验
• 如果一致性比例𝐶𝑅≥0.1，需要修改判断矩阵，直到𝐶𝑅<0.1。

对当前的判断矩阵进行一致性检验：当前判断矩阵的=4.68，n=4，求得𝐶𝐼 = 0.227，查表𝑅𝐼=0.89，得𝐶𝑅=0.255，此时𝐶𝑅 ≥0.1，需要修改判断矩阵。

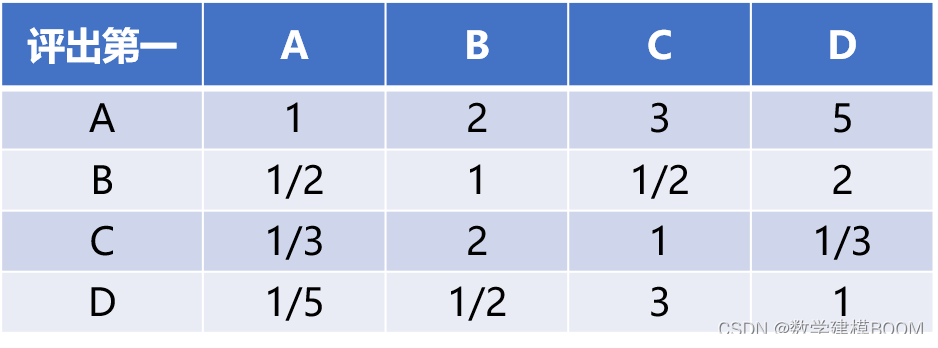
 改了𝑎34改了和a43后，修改后的矩阵如下：

 对新判断矩阵再进行一致性检验：该判断矩阵的=4.113，𝑛=4，求得𝐶𝐼 = 0.038，查表𝑅𝐼=0.89，得𝐶𝑅=0.042，此时𝐶𝑅 <0.1，通过了一致性检验。

判断矩阵求权重

可以采用算术平均法求权重。此外还有其他方法不多介绍，只掌握一种即可。

将通过了一致性检验的判断矩阵按列归一化，然后每一行分别求和，求和的结果除以𝑛 ，得到的列向量就是权重向量。

求得4项指标的权重依次为0.49，0.18，0.23，0.1。

问题

已经求出权重了，对所有准则进行加权求和，每一位up主的综合评分 = 0.49粉丝数+0.18播放数+0.23获赞数+0.1稿件数。

注意，该式中的数据是归一化处理后的数据。

结果如上表所示，最终总评分最高的up就是老番茄。

 总结

层次分析法解决评价类的问题整体思路：

 问题拓展

本例题当中，粉丝数等指标的数据是已知的，但在比赛中更常见的情况是指标数据未知，那该怎么办呢？

例如，题目要求以影响力、作品热度、作品质量和发展潜力对up进行综合评价。这四项指标找不到客观数据啊！

此时的解题思路，和本文一样：若准则层有m个因素，则通过构造m个判断矩阵来求出每一个方案层元素的权重，即评分；之后再进行准则层到目标层的操作（即本节课所讲）。

 本文讲解了层次分析法的基本思想，这种更复杂的情况，以及多层准则层的情况该如何处理，会在以后的课程中讲解。