多项式规约——续

①有向图哈密尔顿圈${\le }_p$无向图的哈密尔顿圈
目标：给定一个$n$个节点的有向图$G=(V,E)$，我们可以构造一个含$3n$个顶点的无向图$G^{{}^{\prime }}$。有向图$G$拥有哈密尔顿圈当且仅当无向图$G^{{}^{\prime }}$拥有哈密尔顿圈。
构图思路：把有向图$G$中的一个顶点，拆分成三个顶点(蓝、黑、白)

证明：
$\Rightarrow$
假设$G$存在一个有向的哈密尔顿圈$\Gamma$，那么$G^{{}^{\prime }}$也有一个跟上述顺序一致的无向哈密尔顿圈${\Gamma }^{{}^{\prime }}$。
$\Leftarrow$
假设$G^{{}^{\prime }}$有一个无向哈密尔顿圈${\Gamma }^{{}^{\prime }}$。${\Gamma }^{{}^{\prime }}$访问$G^{{}^{\prime }}$中的顶点必须选择一下两种顺序中的一个：

• 黑，白，蓝
• 黑，蓝，白

${\Gamma }^{{}^{\prime }}$中的黑色节点对应$\Gamma$中的哈密尔顿圈或者逆序中的一个。

②$3-SAT{\le }_p$有向图哈密尔顿圈
目标：给定一个$3-SAT$的实例，我们都能构造出一个图$G$。$3-SAT$实例有解当且仅当图$G$含有一个哈密尔顿圈。
构图思路：

• 图$G$中哈密尔顿圈的个数为$2^n$个，每个文字有真假2种可能，一共有$n$个，从左到右赋值为真，从右到左赋值为假
• 对于每个从句，若存在$x_i$，则增加一个节点，并从左到右增加边；若存在$\overline{x_i}$，则增加一个节点，并从右到左增加边
  

证明：
$\Rightarrow$
假设$3-SAT$实例$\varphi$有满足的真值指派$x^{\ast }$，那么我们在$G$中找到一个哈密尔顿圈$\Gamma$如下：

• 如果$x_i^{\ast }=true$，我们从左到右穿过第$i$行
• 如果$x_i^{\ast }=false$，我们从右到左穿过第$i$行
• 对于每个句子$C_j$，至少存在一行按照我们上述的方向，把句子节点铰接进圈内，我们只把句子节点铰接进圈有且仅有一次。

$\Leftarrow$
假设$G$中有一个哈密尔顿圈$\Gamma$
如果$\Gamma$加入了句子节点$C_j$，并假设与$C_j$前后邻接的节点通过边$e$相连。我们从圈中删除节点$C_j$和其直连边，并用边$e$代替，得到$G-C_j$的哈密尔顿圈。
循环执行上述方法，我们得到在 G − { C 1 , C 2 , … , C k } G-\{C_1,C_2,\dots,C_k\} G−{C1​,C2​,…,Ck​}上的哈密尔顿圈${\Gamma }^{{}^{\prime }}$。
如果${\Gamma }^{{}^{\prime }}$在第$i$行的遍历方向是从左到右的，那么置$x_i^{\ast }=true$，否则置$x_i^{\ast }=false$。
按照上述正确方向遍历进行真值指派，每个句子都会被满足，即原实例$\varphi$可满足。

③$3-SAT{\le }_p$有向图哈密尔顿路径${\le }_p$无向图哈密尔顿路径${\le }_p$最长路径问题
最长路径问题： 给定一个有向图$G=(V,E)$，是否存在包含至少$k$条边的简单路径
证明：
在有向图哈密尔顿圈的构图上，删除从$t$到$s$的边，便得到有向图哈密尔顿路径的实例。有向图哈密尔顿路径可以通过一个节点扩展成三个节点的方式，多项式规约到无向图哈密尔顿路径问题。无向图哈密尔顿路径问题，在原图基础上，令$k=|V|-1$，就可以得到一个最长路径的实例。若包含一个至少为$k=|V|-1$的简单路径，则存在一条哈密尔顿路径。

④哈密尔顿圈问题${\le }_p$TSP问题
TSP问题：给定$n$个城市以及两两城市之间的距离$d(u,v)$，问是否存在一个旅游访问$n$个城市一次且长度$\le D$。
哈密尔顿问题和TSP问题的区别
由于售货员可以从某个城市到其他任何一个城市，因此，该问题对应的是一个完全图（设为G′），而关于判断哈密尔顿回路的图（设为G）并不一定为完全图。
目标：给定一个哈密尔顿圈的实例$G=(V,E)$，创建一个TSP问题的完全图实例，$n$个城市两两间的距离函数定义如下：
$$d(u,v)=\{\begin{array}{rlr}1& & if(u,v)\in E\\ 2& & if(u,v)\notin E\end{array}$$
TSP问题有一个长度$\le n$的旅游当且仅当$G$中含有一个哈密尔顿圈

⑤$3-SAT$问题 ${\le }_p$ 3着色问题
3着色问题：给定一个无向图$G$，问能否用三种颜色给顶点着色，使得邻接顶点间颜色不同。
3着色问题${\le }_p$K寄存器分配问题，对于$k\ge 3$
寄存器分配问题可以建模成$k$着色问题，一个寄存器一个时间只能存一个数据，一个时间点可能涉及多个数据参与运算，此时需要多个寄存器。
目标：给定一个$3-SAT$的实例$\varphi$，我们可以构建一个3着色的实例图$G$。$\varphi$可满足当且仅当$G$是可3着色的。
构图思路：
每个文字连接其对立面，所有文字连接到$B$。对于每个从句，在包含的文字下方，增加6个顶点和13条边。


$\Rightarrow$
若$\varphi$可满足，即每个从句中至少有一个文字是真，赋值为绿色。我们可以在其余两个文字真假都可以的情况下，完成三着色，如下图所示：

$\Leftarrow$
若图$G$可三着色，则$\varphi$是可满足的。
反证法：若$\varphi$是不可满足的，即$\varphi$中文字对应的顶点全部着红色，则推出图$G$不可以三着色。

⑥一般图的三着色${\le }_p$平面图的三着色
注意：一般图的$k$着色仍是$NPC$问题，只不过$k$越大，复杂度的指数底数越小而已，但仍不是多项式时间的。平面图的4着色是$P$问题，最优可$O(n^2)$解决。
目标：任意给出一个图$G$，我们能构造出一个平面图$G^{{}^{\prime }}$。原图$G$可3着色当且仅当平面图$G^{{}^{\prime }}$可三着色。
构图技巧：借助转换小工具，该小工具满足对角着色必须相同

⑦$3-SAT{\le }_p$子集和问题
子集和问题：给定$n$个数$w_1,\dots ,w_n$和整数$W$，是否存在一个子集，其中所有元素的和等于$W$
目标：任给一个$3-SAT$实例$\varphi$，我们都能构造出一个子集和问题的实例。实例$\varphi$可满足当且仅当子集和问题有解
构图思路：任给一个含$n$个变量（每个句子只装3个变量）$k$个句子的$3-SAT$问题的实例$\varphi$，形成$(2n+2k)\times (n+k)$的表格


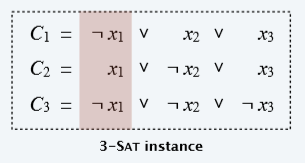
构造解析

• $x_i$和$\overline{x_i}$只能选一个，因此左边$n$列各自和为1（即$W$的前$n$位为1）
• $C_i$中至少有一个文字为真，因此句子本身列的和至少为$1$。为凑够4，从下面 { 1 , 2 } \{1,2\} {1,2}选其中一个或者全选凑够4，选了相应的数，即选中了相应行对应的数。

证明：
$\Rightarrow$
假设实例$\varphi$有一个可满足的真值指派$x^{\ast }$
如果$x_i^{\ast }=true$，选择$x_i$所在行对应的整数；否则选择$\overline{x_i}$对应的整数
每个$x_i$对应的和为1，每个$C_j$对应的和至少为1，加上虚拟的整数，使$C_j$对应的列和为4
这样我们得到一个整数集合，并从整数中找到一个子集，其和为$W$
$\Leftarrow$
假设存在一个子集$S^{\ast }$和为$W$
由于要满足和为$W$，因此子集$S^{\ast }$只能从$x_i$和$\overline{x_i}$中选择一个，不能全选
如果选定$x_i$，则令$x_i^{\ast }=true$，否则令$x_i^{\ast }=false$
同样要满足和为$W$，因此至少从$C_j$中选择一个文字，不然和达不到4.
这样我们就找到了一个可满足的真值指派。

⑧子集和问题${\le }_p$背包问题
背包问题：给定一个物品集合$X$，重量为$u_i\ge 0$，价值$v_i\ge 0$，背包能承受的总重量不超过$U$，给定一个目标价值$V$，是否存在一个子集$S\subseteq X$:
$$\sum _{i\in S}{u}_i\le U,\sum _{i\in S}{v}_i\ge V$$
规约思路：
对于任意一个子集和实例，我们按照如下构造一个背包实例：
$$\{\begin{array}{r}{u}_i=v_i=w_i\\ U=V=W\end{array}$$
这样子集和有解当且仅当背包有解

⑨子集和问题${\le }_p$分割问题
分割问题：给定$m$个数$v_1,v_2,\dots ,v_m$，是否可以将这$m$个数分割成两个子集，使每个子集各元素之和为$\frac{1}{2}{\sum }_i{v}_i$。
构造思路:
给定子集和实例$W,w_1,w_2,\dots ,w_n$，我们构造分割问题如下：
分割问题共有$m=n+2$个元素，元素赋值规则如下：
$$v_1=w_1,v_2=w_2,\dots ,v_n=w_n,v_{n+1}=2\sum _i{w}_i-W,v_{n+2}=\sum _i{w}_i+W$$
由于分割问题总和为$4{\sum }_i{w}_i$，所以$v_{n+1}$和$v_{n+2}$不能在同一子集，不然该子集和为$3{\sum }_i{w}_i$，最终不能均分。要使每部分和为$2{\sum }_i{w}_i$，只能是如下情况：

其中$W$和${\sum }_i{w}_i-W$两部分，说明能从$w_1,w_2,\dots ,w_n$中找到一个子集，使其和为$W$

⑩子集和问题${\le }_p$调度问题
调度问题：给定$n$个任务，任务$j$的处理时间为$t_j$，工作时间发布时间为$r_j$，截止时间为$d_j$，能否找到一个调度方案，使所有任务在一台机器上进行且在相应的时间段$[r_j,d_j]$内完成。
构造方案如下：
构造$n$个任务，任务$j$的处理时间为$t_j=w_j$，发布时间为$r_j=0$，截止时间设为$d_j=1+{\sum }_j{w}_j$
再额外构造任务0，该任务处理时长为$t_0=1$，发布时间为$r_0=W$，截止时间为$d_0=W+1$

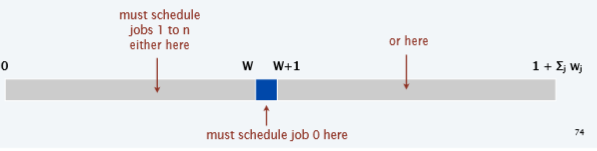
这样就迫使，子集和有解当且仅当调度问题有解