基于物理的渲染：基于图像照明(Image-based Lighting)

在基于物理的渲染方法之中，如果想获得非常好的渲染效果，则需要分析光线的传播来进行全局光照(直接光照与间接光照)的计算，但该方法所需要的计算代价是巨大的，“往往”无法支持实时的需要。相反，如果仅仅考虑光源的直接光照，虽然渲染速度提升，但是渲染质量却不尽如人意，而基于图像照明(IBL)就是这样一种处于两个“极端”之间的方法，把天空盒环境贴图上的颜色信息当做环境光源，通过对反射方程的近似计算，从而生成采样贴图，最终计算光照能量时仅仅需要去对这个贴图进行采样再加以计算即可，相比于完整的全局光照减轻了计算代价，同时也带来了不错的渲染质量的提升，以下本文便会详细介绍这样一种渲染技术。

1 预备知识

(在第一章中回顾一些简略的基础知识，详细讲解可以查看我的前几篇笔记)
根据learnopengl中定义，一般把满足如下三个条件的渲染称为基于物理的渲染：
1.基于微平面理论
2.使用基于物理的BRDF
3.保证能量守恒

1.1 微平面理论

所谓微平面理论(Microfacets Theory)，就是从微观的角度去观察物体，并认为物体的表面在到达微观的尺度之后，都是由许许多多的更小的理想镜面所组成的。
当这些微小的理想镜面的法线方向较为集中一致的时候，从宏观角度来看，物体的镜面反射会比较明显，反之，当这些微小镜面的法线方向较为杂乱的时候，物体表面则会相对粗糙。如下图所示：

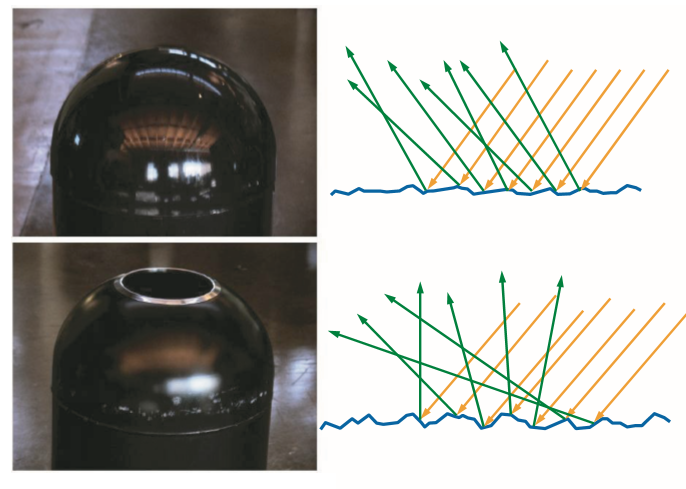
（可以看到，第一幅图的微平面的镜面法线方向比较集中，第二幅图中的微平面的镜面法线方向比较分散）
当然并不是所有的光都会被微表面直接反射的。当光线照射到物体表面时，一部分光线会与表面的许许多多的微小镜面发生镜面反射，另一部分光线则会折射进入物体内部，如下图：

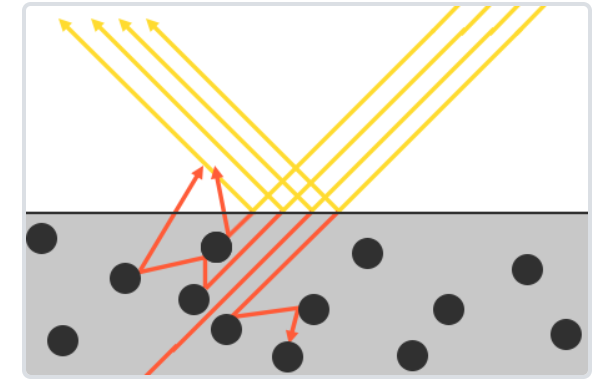
当光线折射进入内部的时，会与物体的微小粒子不断发生碰撞并散射到随机方向，在碰撞的过程中一部分光线会被吸收转换为热能，还有一部分光线会因为散射方向的随机性重新离开表面，而这部分光线就恰好形成了漫反射。

1.2 反射方程与BRDF

具体来说，上述所讲的微平面理论会体现在反射方程当中的BRDF中。
首先回顾一下反射方程：
$$L_o\left(p,{\omega }_o\right)={\int }_{{\Omega }^{+}}{L}_i\left(p,{\omega }_i\right)f_r\left(p,{\omega }_i,{\omega }_o\right)\left(n\cdot {\omega }_i\right)\mathrm{d}{\omega }_i$$
其中$p$为光线照射到的点，$L_i$为入射光，$L_o$为观察方向的出射光，${\omega }_i和{\omega }_o$又分别代表入射方向与出射方向(观察方向)，$(n\cdot {\omega }_i)$代表宏观物体法线与入射光的夹角。$f_r$即BRDF，用来衡量入射光radiance与出射光irradiance的比例。因此直观理解的反射方程，即来自观察方向${\omega }_r$上的反射光，是由所有不同方向上入射光贡献得到的，而不同方向入射光对反射方向${\omega }_r$的贡献程度则由物体表面材质属性决定，所以乘上了一个BRDF函数来体现这一点。
正如一开始所说，对于基于物理与微平面理论的特点，就体现在BRDF之上，一般使用的微平面模型为Cook-Torrance模型，其BRDF为：
$$f_r\left({\omega }_i,{\omega }_o\right)=k_d{f}_{lambert}+f_s$$
其中：
$$\begin{array}{rl}& f_{lambert}=\frac{\rho }{\pi }\\ & f_s=\frac{FDG}{4(N\cdot V)(N\cdot L)}\\ & k_s=F\\ & k_d=(1-k_s)\ast (1-matalness)\end{array}$$
$f_{lambert}和f_s$分别代表漫反射项和镜面反射项，$k_s$为微平面理论当中直接与微平面进行镜面反射的光线所占百分比，由菲涅尔项$F$决定，而$k_d$则是折射进物体内部所占的百分比，之所以在$1-k_s$之后乘上了1-metalness (0<metalness<1)，是因为当金属程度越高，镜面反射占比也就越高，而折射进入物体内部的就越少，同时这里的$kd+ks\le 1$也一定程度上保证了能量守恒。对于漫反射项$f_{lambert}$和镜面反射项$f_s$在之前的笔记中有详细推导证明，这里就不再展开。接下来简单介绍一下F,D,G这3个函数

1.2.1 菲涅尔项 F

$F$为菲涅尔项，用来描述光线反射率与 入射光和法线的夹角的关系，精确计算太过复杂，这里一般用近似形式：
$$F\left(h,v,F_0\right)=F_0+\left(1-F_0\right)(1-(h\cdot v){)}^5$$
其中：
$$F_0=lerp(0.04,\rho ,metalness)$$
$v$为观察方向，$h$为微平面法向。$\rho$为物体表面的颜色值，一般由贴图采样决定。

1.2.2 法线分布函数 D

D是法线分布函数，衡量微平面法线的分布情况，物理含义为每单位面积,每单位立体角下所有法向为$h$的微平面的面积。
这里采用GGX/Trowbridge-Reitz作为法线分布函数：
$$D(\mathbf{h})=\frac{{\alpha }^2}{\pi {\left((\mathbf{n}\cdot \mathbf{h}{)}^2\left({\alpha }^2-1\right)+1\right)}^2}$$
其中：
$$\alpha =roughnes{s}^2$$

1.2.3 几何遮挡函数 G

G是几何函数，为了表示微平面的自遮挡从而引起的光线损失，如下图所示：

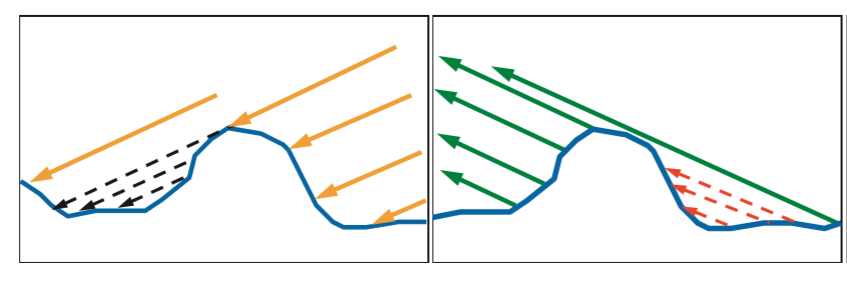
左边一幅图中是入射光线无法照射到一些微平面，这种情况称为Shadowing，右边图中是反射光线无法正常到达人眼，称为Masking，而几何函数G正是为了模拟出这两种情况所导致的光线损失，在UE4中采用了Schlick-GGX来进行建模：
$$\begin{gathered} G_1(\mathbf{v})=\frac{\mathbf{n}\cdot \mathbf{v}}{(\mathbf{n}\cdot \mathbf{v})(1-k)+k} \\ G(\mathbf{l},\mathbf{v})=G_1(\mathbf{l})G_1(\mathbf{v}) \end{gathered}$$
其中：
$$\begin{gathered} k=\frac{\alpha }{2} \\ \alpha =roughnes{s}^2 \end{gathered}$$
(注：这里仅仅使用IBL作为光源)

2 基于图像的照明 IBL

不如想象这样一个场景：所有需要渲染的模型都处于一个巨大的球体的中心，球体上的每一个点都会发出光线照射模型，因为球体的相对"巨大"，所以模型之上的相对移动都可以忽略，因此对于模型上的每一点能接收到来自球体的光线都由其法线所在半球决定，如下图所示：

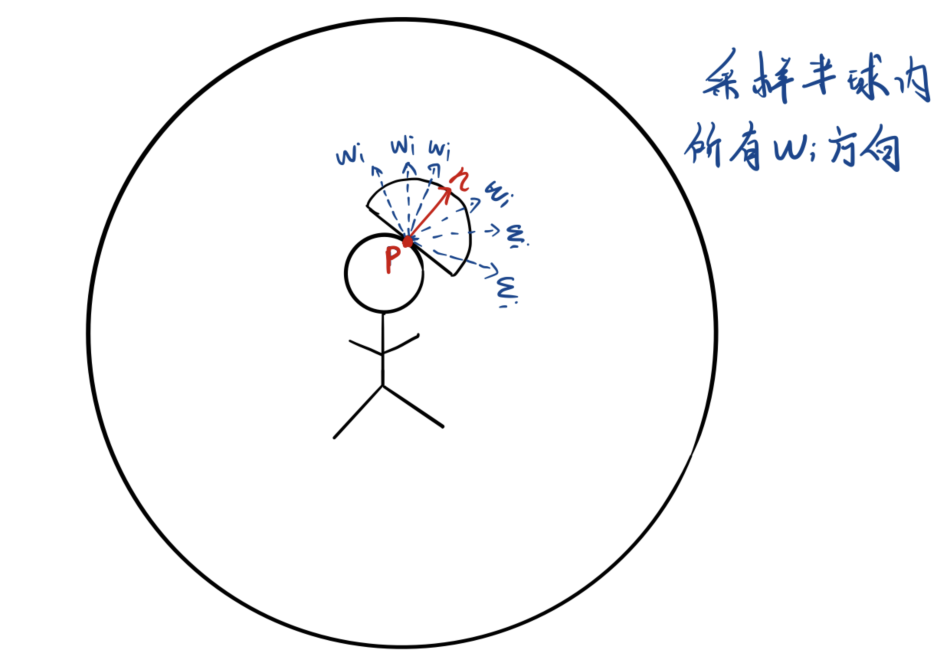
对于一个如下图这样的天空盒只需要给定采样方向就可以获得入射光的辐射度：
（天空盒与球体是互通的）

采样结果：$L_i\left(p,{\omega }_i\right)=\mathrm{cubeSampling}\left({\omega }_i\right)$

以上正是基于图像的照明的想法，正如开篇所讲其实就是利用了整个天空盒贴图来当作光源，以更多的环境光源来提升渲染的质量，这里的难点就是，如果我们每算一个点都要去用该点法线所在半球的所有方向来采样天空盒，获得辐射度结果，来充当反射方程的入射光$L_i$，其计算代价依然是巨大的，因此会利用近似和一些预计算的方法来将部分计算结果存储为一张贴图，在真正渲染的时候，通过贴图的采样来辅助计算加快速度。接下来我们将反射方程分解成漫反射部分和镜面反射部分来进行讨论。

2.1 漫反射部分

将第一章提到的Cook-Torrance BRDF 带入反射方程得到：
$$L_o\left(p,{\omega }_o\right)={\int }_{{\Omega }^{+}}(k_d{f}_{lambert}+f_s)L_i\left(p,{\omega }_i\right)\left(n\cdot {\omega }_i\right)\mathrm{d}{\omega }_i$$
进一步，将反射方程展开：
$$L_o\left(p,{\omega }_o\right)={\int }_{{\Omega }^{+}}{k}_d{f}_{lambert}{L}_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i+{\int }_{{\Omega }^{+}}{f}_s{L}_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i$$
其中左半部分即为漫反射部分，右半部分即为镜面反射部分，首先考虑漫反射部分，同时将$f_{lambert}=\frac{\rho }{\pi }$带入：
$$L_d\left({\omega }_o\right)=\frac{\rho }{\pi }{\int }_{{\Omega }^{+}}{k}_d{L}_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i$$
其中$k_d=(1-k_s)\ast (1-matalness)$,而$k_s=F(h,v)$，其中微平面法向$h=({\omega }_i+{\omega }_o)/||{\omega }_i+{\omega }_o||$,包含积分项，所以$k_d$不能直接提出积分，这里为了简化将其做了一步近似，将$k_s$改为：
k s = F 0 + ( m a x { 1 − r o u g h n e s s , F 0 } − F 0 ) ( 1 − ( n ⋅ ω o ) ) 5 k_s = F_{0}+\left(max\{1-roughness,F_0\}-F_{0}\right)(1-(n \cdot \omega_o))^{5} ks​=F0​+(max{1−roughness,F0​}−F0​)(1−(n⋅ωo​))5
与原始式子相比有两个区别：
1.第一个括号的$(1-F_0)$替换为了 ( m a x { 1 − r o u g h n e s s , F 0 } − F 0 ) (max\{1-roughness,F_0\}-F_{0}) (max{1−roughness,F0​}−F0​)
2.第二个括号的$h\cdot v$替换为了$n\cdot {\omega }_o$
因此此时$k_d$也与积分项无关，提出得到：
$$L_d\left({\omega }_o\right)\approx k_d\frac{\rho }{\pi }{\int }_{\Omega }{L}_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i$$
现在漫反射项的积分值仅仅取决于法线向量$n$，因为正如本章一开始的火柴人示意图所示，$n$所在半球会决定所有的${\omega }_i$方向。

对于积分的计算可以直接使用蒙特卡洛积分的方法，在$n$所在的半球上均匀采样来算出无偏的积分近似解(这里把$1/\pi$也丢了进去)：
$$\begin{array}{rl}\frac{1}{\pi }{\int }_{\Omega }{L}_i\left(p,{\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i& =\frac{1}{\pi }{\int }_0^{2\pi }{\int }_0^{\frac{\pi }{2}}{L}_i\left({\omega }_i\right)\cos \theta \sin \theta \mathrm{d}\theta \mathrm{d}\varphi \\ & \approx \frac{1}{\pi }\frac{1}{N_1{N}_2}\sum _i^{N_1}\sum _j^{N_2}\frac{L_i\left({\varphi }_j,{\theta }_i\right)\cos \left({\theta }_i\right)\sin \left({\theta }_i\right)}{pdf(\theta )pdf(\varphi )}\end{array}$$
将$pdf(\theta )=\frac{1}{0.5\pi },pdf(\varphi )=\frac{1}{2\pi }$带入化简最终得到
$$\frac{1}{\pi }{\int }_{\Omega }{L}_i\left(p,{\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i=\pi \frac{1}{N_1{N}_2}\sum _i^{N_1}\sum _j^{N_2}{L}_i\left({\varphi }_j,{\theta }_i\right)\cos \left({\theta }_i\right)\sin \left({\theta }_i\right)$$
只要遍历所有法线方向，再利用上式计算出每个法线向量所对应的结果，存储在贴图中即可，称该贴图为irradiance map。同样不难想象，因为遍历了所有法线方向，存储下来的贴图依然是一个6张的天空盒贴图：

当然最终实际渲染的时候，也是利用法线$n$对irradiance map直接进行采样，再乘上$k_d\rho$即可得到完整漫反射项近似结果。
这里附上c++实现以供参考：
generate_irradiance_map

2.2 镜面反射部分

根据反射方程，镜面反射部分如下：
$$L_s({\omega }_o)={\int }_{{\Omega }^{+}}{f}_s({\omega }_o,{\omega }_i)L_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i$$
其中：
$$f_s=\frac{FDG}{4(N\cdot {\omega }_o)(N\cdot {\omega }_i)}$$
此时的积分值会因为$f_s$的存在，依赖于更多的变量，如法向$n$, 观察方向${\omega }_o$,粗糙度，金属度等等，所以对于该积分的预计算要远比漫反射部分来的棘手，这里我们采用虚幻4所提出来的Spilt Sum Aprroximation，分解如下：

${\int }_{{\Omega }^{+}}{f}_s({\omega }_o,{\omega }_i)L_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i\approx \left(\frac{{\sum }_k^N{L}_i\left({\omega }_i^{(k)}\right)(n\cdot {\omega }_i^{(k)})}{{\sum }_k^N(n\cdot {\omega }_i^{(k)})}\right)\left(\frac{1}{N}{\sum }_j^N\frac{f_s\left({\omega }_i^{(j)},{\omega }_o\right)\left(n\cdot {\omega }_i^{(j)}\right)}{pdf\left({\omega }_i^{(j)}\right)}\right)$
接下来对这个分解进行分析

2.2.1 prefilter environment map

(以下推导证明，很大程度参考了Upba的文章，我这里再添加了一些细节的推导过程，感谢大佬的文章)
仔细观察近似之后式子的右半部分，不难发现其实是一个蒙特卡洛积分的形式，我们将其还原：
$$\frac{1}{N}\sum _j^N\frac{f_s\left({\omega }_i^{(j)},{\omega }_o\right)\left(n\cdot {\omega }_i^{(j)}\right)}{pdf\left({\omega }_i^{(j)}\right)}\approx {\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)n\cdot {\omega }_{i}d{\omega }_i$$
如此，不难进一步推导出，对于分解之后左边括号的内容其实是对这样一个式子的近似：
$$\frac{{\sum }_k^N{L}_i\left({\omega }_i^{(k)}\right)(n\cdot {\omega }_i^{(k)})}{{\sum }_k^N(n\cdot {\omega }_i^{(k)})}\approx \frac{{\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)L_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i}{{\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)n\cdot {\omega }_{i}d{\omega }_i}$$
以下我们暂且把右边部分放在一旁，首先解释分解的左边部分。利用蒙特卡洛积分的方法，将分子和分母分别展开：
$$\frac{{\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)L_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i}{{\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)n\cdot {\omega }_{i}d{\omega }_i}\approx \frac{\frac{1}{N}{\sum }_k^N\frac{f_s({\omega }_i^{(k)},{\omega }_o)L_i\left({\omega }_i^{(k)}\right)\left(n\cdot {\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}{\frac{1}{N}{\sum }_k^N\frac{f_s({\omega }_i^{(k)},{\omega }_o)\left(n\cdot {\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}$$
将$f_s({\omega }_i^{(k)},{\omega }_o)=\frac{D\left({\omega }_h^{(k)}\right)F\left({\omega }_o,{\omega }_h^{(k)}\right)G\left({\omega }_o,{\omega }_i^{(k)}\right)}{4({\omega }_o\cdot n)({\omega }_i^{(k)}\cdot n)}$代入化简可得：
$$\begin{array}{rl}\frac{\frac{1}{N}{\sum }_k^N\frac{f_s({\omega }_i^{(k)},{\omega }_o)L_i\left({\omega }_i^{(k)}\right)\left(n\cdot {\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}{\frac{1}{N}{\sum }_k^N\frac{f_s({\omega }_i^{(k)},{\omega }_o)\left(n\cdot {\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}& =\frac{\frac{1}{N}{\sum }_k^N\frac{D\left({\omega }_h^{(k)}\right)F\left({\omega }_o,{\omega }_h^{(k)}\right)G\left({\omega }_o,{\omega }_i^{(k)}\right)L_i\left({\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}{\frac{1}{N}{\sum }_k^N\frac{D\left({\omega }_h^{(k)}\right)F\left({\omega }_o\cdot {\omega }_h^{(k)}\right)G\left({\omega }_o,{\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}\\ & =\frac{\frac{1}{N}{\sum }_k^N\frac{D\left({\omega }_h^{(k)}\right)F\left({\omega }_o,{\omega }_h^{(k)}\right)G_1\left({\omega }_i^{(k)}\right)L_i\left({\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}{\frac{1}{N}{\sum }_k^N\frac{D\left({\omega }_h^{(k)}\right)F\left({\omega }_o\cdot {\omega }_h^{(k)}\right)G_1\left({\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}\end{array}$$

接下来对概率密度函数$pdf({\omega }_i^{(k)})$进行推导：
首先根据法线分布函数$D$的定义，有如下式子成立：
$${\int }_{{\mathcal{H}}^2}\cos \theta D\left({\mathbf{\omega }}_h\right)\mathrm{d}{\mathbf{\omega }}_h=1$$
其中$\theta$为微平面法向${\omega }_h$与宏观法向$n$的夹角。从几何角度很容易解释这个等式，即微平面的面积投影至宏观平面上，大小与宏观角度的面积元大小一致。(详细解释可参考我的cook-torrance brdf推导那篇文章)
而我们都知道的一点是，pdf在其整个积分域的积分值为1，所以该积分式中的被积项$\cos \theta D\left({\mathbf{\omega }}_h\right)$即${\omega }_h$的pdf，这与想要求得的${\omega }_i$的pdf并不一致，所以需要进一步得到$\mathrm{d}{\omega }_h$与$\mathrm{d}{\omega }_i$的关系：

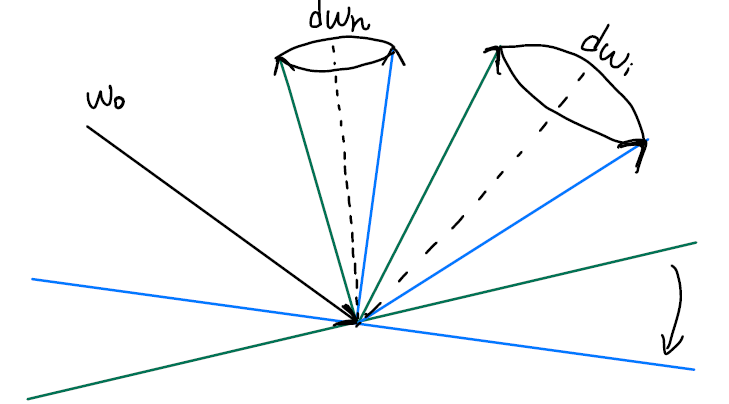
首先固定入射方向${\omega }_o$，微分立体角$d{\omega }_h$是一个很小的范围，那么反推回去，这样一个很小的范围所对应的入射角自然也是一个很小的范围$d{\omega }_i$，形象的来看，就是转动平面得到所有微观法线在$d{\omega }_h$范围之内的平面，通过这些微平面，所得到的入射范围。为了寻求二者的关系，以入射方向${\omega }_o$为$z$轴负方向，建立球面坐标系如下：

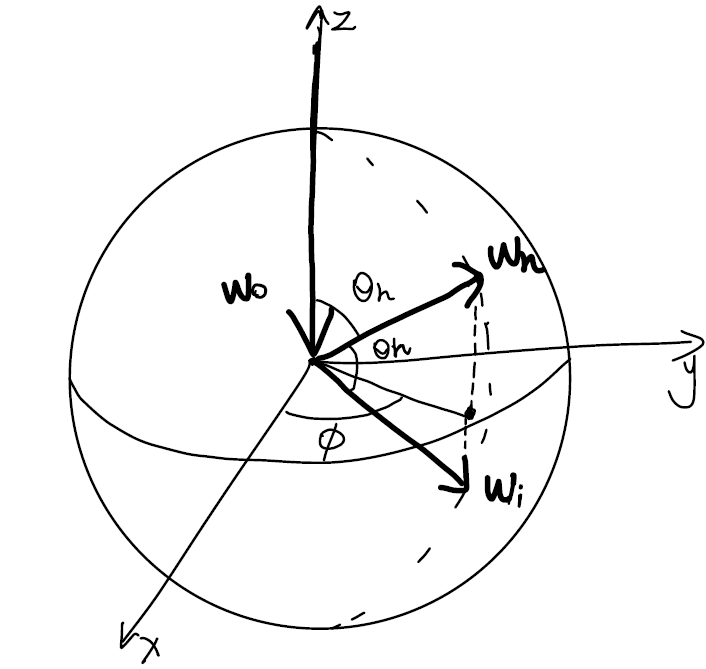
根据图中的单位球面坐标系以及标注的角度，不难得出${\omega }_h$的球面坐标为(1，${\theta }_h$，$\varphi$)，则不难计算出微分立体角

$d{\omega }_h=sin{\theta }_{\mathrm{h}}\mathrm{d}{\theta }_{\mathrm{h}}\mathrm{d}\varphi$

同时${\omega }_i$的球面坐标为(1，2${\theta }_h$，$\varphi$)，因为$\theta$角变为两倍，那么对于${\omega }_i$来说$\theta$角度的微分变化应该也为两倍，因此计算得到

$d{\omega }_i=sin2{\theta }_h\ast 2d{\theta }_h\ast d\varphi =4sin{\theta }_{h}cos{\theta }_{h}d{\theta }_{h}d\varphi$

此时已经知道了$d{\omega }_h$与$d{\omega }_o$，那么

$$d{\omega }_h=\frac{d{\omega }_i}{4cos{\theta }_h}$$

将其带入${\omega }_h$的pdf积分式子中得：

$${\int }_{{\mathcal{H}}^2}\cos \theta D\left({\mathbf{\omega }}_h\right)\frac{d{\omega }_i}{4cos{\theta }_h}=1$$
因此，最终得到$pdf({\omega }_i)=\frac{\cos \theta D\left({\mathbf{\omega }}_h\right)}{4cos{\theta }_h}$,需要注意得是其中$\theta$为微平面法向${\omega }_h$与宏观法向$n$的夹角，而${\theta }_h$为${\omega }_i$与${\omega }_o$得夹角，将其带入最开始的式子中，得到：
$$\frac{\frac{1}{N}{\sum }_k^N\frac{D\left({\omega }_h^{(k)}\right)F\left({\omega }_o,{\omega }_h^{(k)}\right)G_1\left({\omega }_i^{(k)}\right)L_i\left({\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}{\frac{1}{N}{\sum }_k^N\frac{D\left({\omega }_h^{(k)}\right)F\left({\omega }_o\cdot {\omega }_h^{(k)}\right)G_1\left({\omega }_i^{(k)}\right)}{pdf\left({\omega }_i^{(k)}\right)}}=\frac{{\sum }_k^N\frac{F\left({\omega }_o,{\omega }_h^{(k)}\right)G_1\left({\omega }_i^{(k)}\right)L_i\left({\omega }_i^{(k)}\right)\left({\omega }_o\cdot {\omega }_h^{(k)}\right)}{{\omega }_h^{(k)}\cdot n}}{{\sum }_k^N\frac{F\left({\omega }_o,{\omega }_h^{(k)}\right)G_1\left({\omega }_i^{(k)}\right)\left({\omega }_o\cdot {\omega }_h^{(k)}\right)}{{\omega }_h^{(k)}\cdot n}}$$
出于以下两点考虑，约去分子分母的菲涅尔项的$F$
1.当物体表面比较光滑时，采样的${\omega }_h$都十分接近${\omega }_o$所以$F$几乎时一个变化不大的定值，故可以约去
2.当物体表面比较粗糙时，最终的radiance计算结果也会比较粗略，加不加$F$影响不大
经过上述的一系列近似化简过程我们得到：
$$\frac{{\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)L_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i}{{\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)n\cdot {\omega }_{i}d{\omega }_i}\approx \frac{{\sum }_k^N\frac{G_1\left({\omega }_i^{(k)}\right)L_i\left({\omega }_i^{(k)}\right)\left({\omega }_o\cdot {\omega }_h^{(k)}\right)}{{\omega }_h^{(k)}\cdot n}}{{\sum }_k^N\frac{G_1\left({\omega }_i^{(k)}\right)\left({\omega }_o\cdot {\omega }_h^{(k)}\right)}{{\omega }_h^{(k)}\cdot n}}$$
虚幻4在此之上做了进一步的假设，即令${\omega }_{\mathbf{o}}=\mathbf{n}=\mathbf{R}$，该假设是因为：对于镜面反射的brdf$f({\omega }_i,{\omega }_o)$，只会在反射方向$R$的附近有值，如下图中波瓣所示：

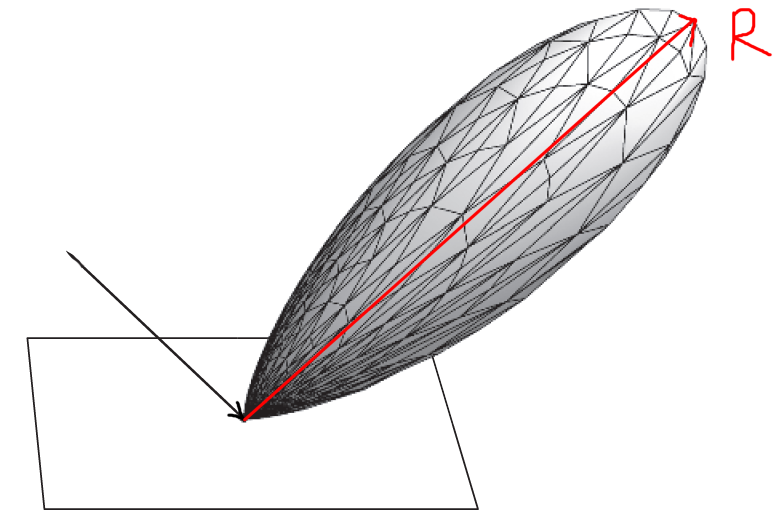
在不同方向入射时(除掠角)，波瓣的变化不大，所以会有：
$$f\left({\omega }_o,{\omega }_i(\mathbf{n}),\mathbf{n}\right)\approx f\left(\mathbf{R},{\omega }_i(\mathbf{R}),\mathbf{R}\right)$$
转变示意图：

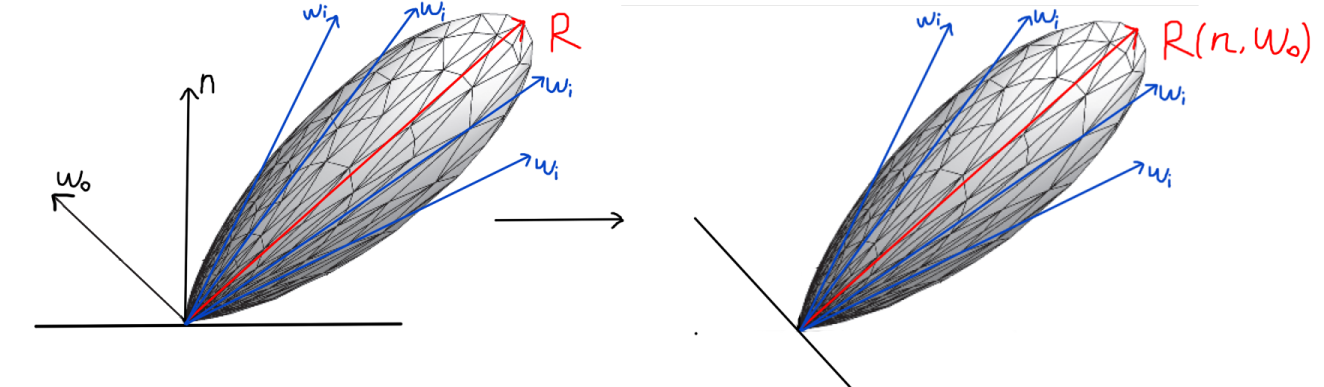
(注意这里的${\omega }_i$是根据法线分布采样出法线，再根据观察方向反推得到的)
将假设带入原积分式子得：
$$\frac{{\int }_{\Omega (\mathbf{n})}{f}_s\left({\omega }_i,{\omega }_o\right)L_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i}{{\int }_{\Omega (\mathbf{n})}{f}_s\left({\omega }_i,{\omega }_o\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i}\approx \frac{{\int }_{\Omega (\mathbf{R})}{f}_s\left({\omega }_i,\mathbf{R}\right)L_i\left({\omega }_i\right)\mathbf{R}\cdot {\omega }_i\mathrm{d}{\omega }_i}{{\int }_{\Omega (\mathbf{R})}{f}_s\left({\omega }_i,\mathbf{R}\right)\mathbf{R}\cdot {\omega }_i\mathrm{d}{\omega }_i}\triangleq L_c(\mathbf{R})$$
其中：
$$\begin{array}{rl}{L}_c(\mathbf{R})& \approx \frac{{\sum }_k^N\frac{G_1\left({\omega }_i^{(k)}\right)L_i\left({\omega }_i^{(k)}\right)\left(\mathbf{R}\cdot {\omega }_h^{(k)}\right)}{{\omega }_h^{(k)}\cdot \mathbf{R}}}{{\sum }_k^N\frac{G_1\left({\omega }_i^{(k)}\right)\left(\mathbf{R}\cdot {\omega }_h^{(k)}\right)}{{\omega }_h^{(k)}\cdot \mathbf{R}}}\\ & =\frac{{\sum }_k^{N}L\left({\omega }_i^{(k)}\right)G_1\left({\omega }_i^{(k)}\right)}{{\sum }_k^N{G}_1\left({\omega }_i^{(k)}\right)}\end{array}$$
呼~！
经过一众的近似化简推导之后，我们终于得到了与虚幻4所给出的分解十分相似的结果，不过害有一点不一样的是，虚幻4中用$n\cdot {\omega }_i$代替了这里的$G_1({\omega }_i)$，但考虑到二者的变化趋势与值域范围都是相似的，这种近似也是可以理解的。
因此最终对于这部分需要预计算的内容就是：
$$L_c(\mathbf{R})\approx \frac{{\sum }_k^N{L}_i\left({\omega }_i^{(k)}\right)(\mathbf{R}\cdot {\omega }_i^{(k)})}{{\sum }_k^N(\mathbf{R}\cdot {\omega }_i^{(k)})}$$
由于假设了${\omega }_{\mathbf{o}}=\mathbf{n}=\mathbf{R}$，此时该式子仅有两个变量$\mathbf{R}$和粗糙度roughness(不同的粗糙度会导致${\omega }_i$的采样结果不同),因此只要固定粗糙度，就可以像irradiance map那样计算出一个预计算的天空盒的6张贴图，一般情况下会设定计算0,0.25,0.5,0.75,1.0共计5个粗糙度等级的情况下的cubemap，最终采样的时候可以选粗糙度最近的cubemap进行双线性插值，也可以利用粗糙度进行三线性插值。不同粗糙度的计算结果图如下：

需要注意的是这里与irradiance map不同的是需要使用反射方向$\mathbf{R}$来进行cubemap的采样，附上c++实现：
generate_prefilter_map

2.2.2 BRDF LUT

再观察这个分解的式子：

${\int }_{{\Omega }^{+}}{f}_s({\omega }_o,{\omega }_i)L_i\left({\omega }_i\right)n\cdot {\omega }_i\mathrm{d}{\omega }_i\approx \left(\frac{{\sum }_k^N{L}_i\left({\omega }_i^{(k)}\right)(n\cdot {\omega }_i^{(k)})}{{\sum }_k^N(n\cdot {\omega }_i^{(k)})}\right)\left(\frac{1}{N}{\sum }_j^N\frac{f_s\left({\omega }_i^{(j)},{\omega }_o\right)\left(n\cdot {\omega }_i^{(j)}\right)}{pdf\left({\omega }_i^{(j)}\right)}\right)$
其中左半部分已经在上一节中给出了详细解释，右半部分本质就是一个蒙特卡洛积分的形式，还原之后形式如下：
$$\frac{1}{N}\sum _j^N\frac{f_s\left({\omega }_i^{(j)},{\omega }_o\right)\left(n\cdot {\omega }_i^{(j)}\right)}{pdf\left({\omega }_i^{(j)}\right)}\approx {\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)n\cdot {\omega }_{i}d{\omega }_i$$
此时积分中含有的变量为：$F_0,{\omega }_o,n$和粗糙度，由于这里考虑的是各向同性的情况，所以针对于${\omega }_o,n$只需要用二者之间的夹角$\theta$作为变量即可。但3个变量的存在依然不理想，接下来需要做的就是想办法消去$F_0$使得预计算成为可能。
在这里对它重新进行推导：
$$\begin{array}{rl}{\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)n\cdot {\omega }_{i}d{\omega }_i=& {\int }_{{\Omega }^{+}}{f}_s\left({\omega }_i,{\omega }_o\right)\frac{F\left({\omega }_o,h\right)}{F\left({\omega }_o,h\right)}n\cdot {\omega }_{i}d{\omega }_i\\ =& {\int }_{{\Omega }^{+}}\frac{f_s\left({\omega }_i,{\omega }_o\right)}{F\left({\omega }_o,h\right)}\left(F_0+\left(1-F_0\right){\left(1-{\omega }_o\cdot h\right)}^5\right)n\cdot {\omega }_{i}d{\omega }_i\\ =& F_0{\int }_{{\Omega }^{+}}\frac{f_s\left({\omega }_i,{\omega }_o\right)}{F\left({\omega }_o,h\right)}\left(1-{\left(1-{\omega }_o\cdot h\right)}^5\right)n\cdot {\omega }_{i}d{\omega }_i\\ & +{\int }_{{\Omega }^{+}}\frac{f_s\left({\omega }_i,{\omega }_o\right)}{F\left({\omega }_o,h\right)}{\left(1-{\omega }_o\cdot h\right)}^{5}n\cdot {\omega }_{i}d{\omega }_i\\ =& F_0{\int }_{{\Omega }^{+}}\frac{D({\omega }_h)G({\omega }_o,{\omega }_i)}{4({\omega }_o\cdot n)({\omega }_i\cdot n)}\left(1-{\left(1-{\omega }_o\cdot h\right)}^5\right)n\cdot {\omega }_{i}d{\omega }_i\\ & +{\int }_{{\Omega }^{+}}\frac{D({\omega }_h)G({\omega }_o,{\omega }_i)}{4({\omega }_o\cdot n)({\omega }_i\cdot n)}{\left(1-{\omega }_o\cdot h\right)}^{5}n\cdot {\omega }_{i}d{\omega }_i\\ =& F_0\ast \text{ A}+\text{ B}\end{array}$$
推导的最后一步已经成功的将积分内的$F_0$给提了出去，所以此时的变量仅有$\theta$和粗糙度，因为其二者范围都在0~1，完全可以用一张二维的贴图存储预计算结果，横轴坐标表示$\theta$，纵轴坐标表示粗糙度，对于贴图的颜色值，其中red通道存放A值，green通道存放B值即可，对于A和B的计算依然是利用蒙特卡洛积分即可：
$$\text{ A}\approx \frac{1}{N}\sum _k^N\frac{\frac{D\left({\omega }_h^{(k)}\right)G\left({\omega }_o,{\omega }_i^{(k)}\right)}{4\left({\omega }_o\cdot n\right)\left({\omega }_i^{(k)}\cdot n\right)}\left(1-{\left(1-{\omega }_o\cdot {\omega }_h^{(k)}\right)}^5\right)\left({\omega }_i^{(k)}\cdot n\right)}{pdf\left({\omega }_i^{(k)}\right)}$$
将2.2.1节所推导得到的$pdf({\omega }_i)=\frac{\cos \theta D\left({\mathbf{\omega }}_h\right)}{4cos{\theta }_h}$带入化简可得：

$$\text{ A}\approx \frac{1}{N}\sum _k^N\frac{G\left({\omega }_o,{\omega }_i^{(k)}\right)\left({\omega }_o\cdot {\omega }_h^{(k)}\right)\left(1-{\left(1-{\omega }_o\cdot {\omega }_h^{(k)}\right)}^5\right)}{\left({\omega }_o\cdot n\right)\left({\omega }_h^{(k)}\cdot n\right)}$$
同样不难推导出B：
$$\text{ B}\approx \frac{1}{N}\sum _k^N\frac{G\left({\omega }_o,{\omega }_i^{(k)}\right)\left({\omega }_o\cdot {\omega }_h^{(k)}\right){\left(1-{\omega }_o\cdot {\omega }_h^{(k)}\right)}^5}{\left({\omega }_o\cdot n\right)\left({\omega }_h^{(k)}\cdot n\right)}$$

计算得到的贴图称为LUT，如下：

附上lut计算代码：
IntegrateBRDF

最后在真正渲染时，计算某个点着色的过程只需要对贴图采样再加以计算即可：
$$L\left({\omega }_o\right)=k_d\rho \text{IrradianceMap}(\mathbf{n})+\text{PrefilterMap}(\mathbf{R})\left(F_0\ast \text{ A }+\text{ B}\right)$$
伪代码:

vec3 ibl_fragment_shader()
{
	vec3 f0 = lerp(vec3(0.04), albedo, metalness);
	vec3 F = fresenlschlick_roughness(wo, normal, f0, roughness);
	vec3 kS = F;
	vec3 kD = (1 - metalness) * (vec3(1) - kS);
	
	//diffuse
	vec3 irradiance = cubemap_sample(irradianceMap, normal);
	vec3 diffuse = irradiance * kD * albedo;
	
	//prefilter
	vec3 R = reflect(wo, normal);
	int specular_miplevel = (int)(roughness * max_mip_level + 0.5f);
	vec3 prefilter_color = cubemap_sample(prefilterMap, R, specular_miplevel );
	
	//lut
	vec2 temp= texture_sample(brdfLUT, n_dot_v, roughness);
	float A = temp.x, B = temp.y;
	
	//specular
	vec3 specular = f0 * A + vec3(B, B, B);
	specular = cwise_product(prefilter_color, specular);
	
	vec3 result= kD * diffuse + specular;
	return result;
}

3 总结

以上就是IBL的所有过程了，不难看出为了得到实时的效果，在计算镜面反射项的时候进行了大量的近似，误差主要来源就是这里，但利用IBL对渲染效果提升是巨大的，可以看几张渲染图：


最后再贴一下我自己写的软光栅渲染器吧：

SRender
简单的Blinn-Phong模型与IBL都有实现。包括一些其它的图形学基础算法，这里就不在列举了。
主要特点是纯C++实现，没有任何依赖，核心代码大概在2000多行，因此比较适合阅读与学习，如果有任何错误与问题也欢迎指正交流！

Reference

[1]Ubp.a:深入理解 PBR/基于图像照明 (IBL)
[2]moriya苏蛙可:DX12渲染管线(1) - 基于物理的渲染(PBR)
[3] LearnOpenGL
[4] Real shading in Unreal Engine 4
[5] Background: Physics and Math of Shading by Naty Hoffmann