Wannafly交流赛1 C、腰带图

题目链接：https://www.nowcoder.com/acm/contest/69/C

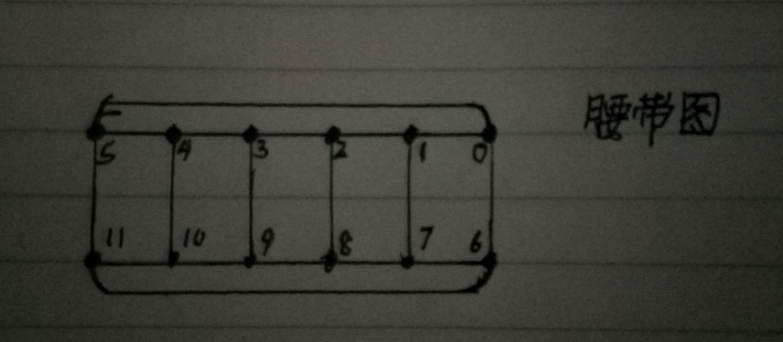
腰带图等价于立体意义上的棱柱；具体：点p0……p（n/2-1）依次围成环，点pn2……p（n-1）依次围成环；点依次对应连接；

例：12点的腰带图如下所示

编程序，判断是否n点3n/2边的平面图是否为腰带图；

*首先需要得到第一个正方形，因为不按顺序，我们不妨令p0=0，第一个正方形为0-1-7-6，对应点pn/2应该选择与p0相连的三点1、6、5；分别遍历三种可能情况：

   p1是p0相连的点(非p6），p7是p6相连的点(非p0） 

   如图p6=1时，那么p1=6，p7=7，下面正方形p1-p2-p8-p7，因为p8必须与p7相连，与p7相连的两个点1、6定好了，p8=8，同理p2=11，点8与点11不相连，所以会判断失败！

   如图p6=6时，那么p1=1，p7=7，接下来正方形p1-p2-p8-p7，因为p8必须与p7相连，与p7相连的两个点1、6定好了，

p8=8，同理p2=2，是相连的！继续下去！

*第一个正方形确定后，接下来的正方形都是对应环前点相连三点中未确定的剩下的最后一点，仅需判断其是否相连，不相连不可能是腰带图，判断失败，相连就继续下去！

*带子形成，还要判断p0与p（n/2-1）是否相连，pn/2与p（n-1）是否相连；（我比赛时，忽略了这点，WA！）

  以上判断都未曾失败，即腰带图已经顺序码好了！

程序：三种p0-pn/2枚举方案，判断函数is_Map( )做到如下三点：

        *首先是否能定下第一个正方形

        *能不能无误依次定下所有正方形，形成带状

        *首尾是否对应相连形成环状

        

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <math.h>
#include <vector>
#include <string.h>
#define Size 300
using namespace std;

int n,m,cnt;
vector <int> V[Size];
int flag[Size][Size];
int ans[Size];
int vis[Size];
void init(){
    cnt=0;
    memset(vis,0,sizeof(vis));
    memset(flag,0,sizeof(flag));
    for(int i=0;i<n;++i) V[i].clear();
}
int NextDout(int x){
    for(int i=0;i<3;++i)
        if(!vis[V[x][i]] )return V[x][i];
    return -1;
}

void Printf(){
    printf("%d",ans[0]);
    for(int i=1;i<n;++i)
        printf(" %d",ans[i]);
    printf("\n");
}

bool is_Map(int a,int b){
    memset(vis,0,sizeof(vis));
    //第1个正方形
    cnt=2;
    vis[a]=vis[b]=1;
    ans[0]=a;ans[n/2]=b;
    for(int i=0;i<3&&cnt!=4;++i)
        for(int j=0;j<3;++j){
            int A=V[a][i];
            int B=V[b][j];
            if(A!=b&&B!=a&&flag[A][B]){
                vis[A]=vis[B]=1;
                ans[1]=A;ans[1+n/2]=B;
                cnt=4;break;
            }
        }
    if(cnt!=4)return false;

    //连接下面的正方形
    while(cnt<n){
        int x=NextDout(ans[cnt/2-1]);
        int y=NextDout(ans[cnt/2-1+n/2]);

        if(x==y||x==-1||y==-1||!flag[x][y])return false;
        cnt+=2;
        ans[cnt/2-1]=x;ans[cnt/2-1+n/2]=y;
        vis[x]=vis[y]=1;
    }
    //判断前面2点与后2点是否连成正方形
    if(!flag[ans[0]][ans[n/2-1]]||!flag[ans[n/2]][ans[n-1]])return false;
    Printf();
    return true;
}
void solve(){
    if(n%2==1||m!=n/2*3){printf("-1\n");return;}
    for(int i=0;i<n;++i)
        if(V[i].size()!=3){printf("-1\n");return;}
    for(int i=0;i<3;++i)
        if(is_Map(0,V[0][i]))return;
    printf("-1\n");
}
int main(){
    int T;scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        init();
        int a,b;
        for(int i=1;i<=m;++i){
            scanf("%d%d",&a,&b);
            V[a].push_back(b);
            V[b].push_back(a);
            flag[a][b]=flag[b][a]=1;
        }
        solve();
    }
    return 0;
}