详解基于Encoder-Decoder的seq2seq

最新推荐文章于 2025-03-19 22:18:14 发布

越来越胖的GuanRunwei

最新推荐文章于 2025-03-19 22:18:14 发布

阅读量1.4k

点赞数 3

分类专栏： NLP 深度学习文章标签：自然语言处理深度学习神经网络

本文链接：https://blog.csdn.net/qq_38890412/article/details/120664674

版权

深度学习同时被 2 个专栏收录

32 篇文章

订阅专栏

NLP

16 篇文章

订阅专栏

前言

Seq2seq全称即为sequence to sequence，简而言之就是一个序列转换成另一个序列，它经常会被用于机器翻译这项任务。对于机器翻译这项任务，有一个较为漫长的发展过程。下面我将从传统机器翻译、统计机器翻译以及神经机器翻译三个阶段进行阐述。

传统机器翻译

传统机器翻译主要由两部分实现

构建大量的翻译规则
构建一个大型的双语对照表

这需要大量的经验积累，但人的精力和思想总是有限的，特别是在遇到中文这种有着复杂语法的语言时，传统机器翻译基本就嗝屁了。

统计机器翻译

统计机器翻译，英文Statistics Machine Translation，简称SMT。

巧了，感觉好像又可以使用贝叶斯公式了。

$\large p(y|x)=\frac{p(x|y)p(y)}{p(x)}$

那么，我们想要 $\large argmax_\theta p(y|x)$ ，就只要 $\large argmax_\theta \frac{p(y)p(x|y)}{p(x)}$ ，就只要 $\large argmax_\theta p(y)p(x|y)$ ，总结下来就是 $\large argmax_\theta p(y|x) = argmax_\theta \frac{p(x|y)p(y)}{p(x)} \iff argmax_\theta p(x|y)p(y)$

因为我们只需要找出使得 $\large p(y|x)$ 最大的 $\large \theta$ ，而分母 $\large p(x)$ 作为输入序列的概率，这可以视作一个常数，因此分母 $\large p(x)$ 可以被省略。

在这里， $\large p(x|y)$ 被称作翻译模型(Translation Model)， $\large p(y)$ 被称作语言模型(Language Model)，翻译模型就是指一种语言翻译成另一种语言的模型，它是一种平行翻译的关系，但是光有翻译模型是没有用的，只考虑一句话里的词语而不考虑整句话所有词语的顺序这不是一个好的翻译模型，因此我们需要结合这两种语言模型——TM+LM。

对于TM而言，我们将其再细化一下，从 $\large p(x|y) \rightarrow p(x,a|y)$ ，可以看出我们引入了一个隐变量a，可以将其理解为将句子y利用a的规则或者说是对齐方式翻译为x的概率。

具体什么是对齐方式alignment呢？意思就是在两种语言A和B之间，A的词是跟B的词怎么对应的。很明显，这种对应关系可以是一对一、一对多、多对一、多对多的。比方下图：

这里例子展示了一个法语句子和英语句子词语对齐关系，其中法语词entarte，英文翻译是“hit me with a pie”，英文中根本没有一个词可以直接表示这个含义。中英文中这样的例子更加常见了，有些英文单词可以用一个汉字对应，但也有很多单词需要两个甚至多个汉字对应。另外，同一个词，在不同的语境下，对齐的词和数量都有可能不同，比如“牛”可以对应“cow”也可以对应“awesome”，“cool”可以对应“酷”也可以对应“凉快”。因此，对齐，alignment，是一个十分复杂的东西，学习 $\large p(x,a|y)$ 非常麻烦，我也不太了解，过。

在学习了LM和TM这两个模型之后，是不是就完事儿了呢？当然没有，别忘了公式里还有一个argmax，我们要找出最佳的翻译是什么。根据LM和TM寻找最佳y的过程，就称为“decoding”，即解码。

一个最直接的方法就是，遍历所有可能的y，选择概率最大的那个，当然就是最佳的翻译。明显，这种方式带来的开销是我们无法忍受的。如果学习过CRF或者HMM，我们应该知道对于这种解码的过程，我们一般使用动态规划、启发式搜索的方法来处理。在SMT中具体怎么解码，我们这里也暂时不做深入的研究。

统计机器翻译——SMT，在深度学习时代之前，风光无限，一直是机器翻译的巅峰技术。但是，SMT的门槛也是很高的，那些表现优异的SMT模型，通常都是极其复杂的，里面涉及到大量的特征工程，海量的专家知识，无数的资源积累，繁多的功能模块，还需要庞大的人力去维护。这也是我根本不想去深入了解这个技术的原因。

幸好，在深度学习时代，我们有了更好的方法：神经机器翻译（Neural Machine Translation，NMT）。

神经机器翻译

神经机器翻译，英文Neural Machine Translation，简称NMT，你也可以把它理解为 No Manpower Technology，不需要人力劳动的一种翻译科技。

NMT结构

NMT使用的神经网络结构，是一种被称为sequence-to-sequence的结构，即seq2seq。它还有另外一个常见的名字：Encoder-Decoder结构。这种结构一般都是由两个RNN组成，如下图所示：

其中，

Encoder是将一句话，也就是一个词语序列转换为一个固定长度的向量表示；

Decoder是将这个固定长度的向量表示再转换成我们需要翻译的目标语言的句子或者说是词语序列。

我们可以将其概括成为模型 $\large p(y_1, \cdots, y_{T'} | x_1, \cdots, x_{T})$ ，这边之所以分成 $\large T$ 和 $\large T'$ 两个序列，我们在上文中已经讲过了。

所以Encoder和Decoder总的流程就是，输入单词序列，Encoder通过RNN将单词序列转换为那个C，也就是context vector（上下文向量），这个context vector是对输入序列的一个总结。而后context vector作为输入，输入进Decoder中，Decoder通过RNN将context vector转换为输出序列。其中在Encoder的输入序列中，一个隐层单元是由这个时间点的输入值以及上个时间点的隐层单元决定；在Decoder的输出序列中，本时刻的隐层单元是由上一时刻的隐层单元和上一时刻的输出以及context vector直接影响的，而本时刻的输出是由上一时刻的输出和本时刻的隐层单元以及context vector直接影响的。

NMT隐层单元

Encoder中的隐层单元：

$\large h_{\langle t \rangle} = f(h_{\langle t-1 \rangle}, x_t)$

Decoder中的隐层单元：

$\large h_{\langle t \rangle} = f(h_{\langle t-1 \rangle}, x_t,c)$

Decoder中下一个单词/符号的概率模型为：

$\large p(y_t|y_{t-1},y_{t-2},\cdots,y_1, c) = g(h_{\langle t \rangle},y_{t-1},c)$

( $\large f$ 和 $\large g$ 皆为激活函数，其中对于 $\large g$ 需要再附带一个softmax分类)

目标只有一个找出 $\large \theta$ 使得 $\large \mathop{max}\limits_{\theta} \frac{1}{N}\sum_{n=1}^N logp_\theta(y_n|x_n)$

另一方面，模型也可用于对翻译的输出序列进行评分，分数即为 $\large p_\theta(y|x)$ 。

鉴于简单RNN的梯度不友好性，seq2seq的设计者借鉴了LSTM的思路分别设计了两个门：reset gate 和 update gate

reset gate

$\large r_j = \sigma([W_r x]_j + [U_rh_{\langle t-1 \rangle}]_j)$

其中 $\large \sigma$ 是sigmoid函数， $\large [.]_j$ 表示向量的第j个元素。 $\large x$ 和 $\large h_{t-1}$ 分别为输入以及前一时刻的隐层单元，相应的， $\large W_r$ 和 $\large U_r$ 是被学习到的权重矩阵。如果reset gate无限接近于0，那么隐层单元会忽略之前的隐层单元的状态而仅仅依赖于本时刻的输入。简而言之，reset gate控制了需要更新的信 $\large h_j^{\langle t \rangle} = z_jh_j^{\langle t-1 \rangle} + (1-z_j)\widetilde{h}_j^{\langle t \rangle}$ 息，0全更新（全忘光），1全不更新。

update gate

$\large z_j = \sigma([W_zx]_j + [U_zh_{\langle t-1 \rangle}]_j)$

update gate控制了有多少信息会从之前的神经元传递到本神经元，简而言之，update gate控制了不被更新的信息的传递，也就是记忆的传递，也就是LSTM中的memory cell。

所以t时刻的隐层单元又可写为

$\large h_j^{\langle t \rangle} = z_jh_j^{\langle t-1 \rangle} + (1-z_j)\widetilde{h}_j^{\langle t \rangle}$ ，分别是记住的和忘记的

这里的 $\large \widetilde{h}_j^{\langle t \rangle} = \phi([Wx]_j + [U(r\odot h_{\langle t-1 \rangle})]_j)$

每个神经元都会训练出对不同时间的信息的依赖。对短期信息比较依赖的会经常使用reset gate，而对长期信息比较依赖则会经常使用update gate。

关于训练和测试时的Decoder

我们发现，在训练和测试时，用到的Decoder是不一样的，那为什么不直接使用训练好的语言模式呢？逼乎上找了张图：

训练时的模式叫做 Teacher Forcing，预测时的模式叫做 Free Running。

难道训练时就必须用teacher forcing，预测时必须用free running模式吗？其实不然。从理论上来讲肯定是可以的，但为什么不这么用呢？在实践中人们发现，这样训练太困难了。因为没有任何的引导，一开始会完全是瞎预测，正所谓“一步错，步步错”，而且越错越离谱，这样会导致训练时的累积损失太大（误差爆炸，exposure bias），训练起来就很费劲。这个时候，如果我们能够在每一步的预测时，让老师来指导一下，即提示一下上一个词的正确答案，decoder就可以快速步入正轨，训练过程也可以更快收敛。因此大家把这种方法称为teacher forcing。所以，这种操作的目的就是为了使得训练过程更容易。

这就好比我们考驾照时，很多教练为了让我们快速通关，会给我们在场地上画上各种标记，告诉我们你看到某个标记就执行某个动作（可以说是作弊手段）。这种方法很有效，我们在练车的时候，死记住这些作弊技巧，很容易在训练场顺利倒车、侧方停车。但这种方法在我们上考场的时候就会暴露出问题了——考场上可没人给你做标记！因此很多人明明在下面自己练车的时候很顺，以上考场就挂了。这也是teacher forcing方法的一个弊端：预测时我们没有老师给你做标记了！纯靠自己很可能挂掉。

所以，更好的办法，更常用的办法，是老师只给适量的引导，学生也积极学习。即我们设置一个概率p，每一步，以概率p靠自己上一步的输入来预测，以概率1-p根据老师的提示来预测，这种方法称为计划采样（scheduled sampling）：

这是种什么感觉呢？就拿我们来刷LeetCode来说吧，完全不看答案的话，对于我来说的话就太难了。。。做题的进度会灰常慢，如果我完全看答案写，那也没啥意义，过几天就忘了，所以最好的方式就是自己也思考，遇到太难的时候就看看答案，这样我们又能保证进度，又能有学习效果。

另外有一个小细节：在seq2seq的训练过程中，decoder即使遇到了<end>标识也不会结束，因为训练的时候并不是一个生成的过程，我们需要等到“标准答案”都输入完才结束。

seq2seq损失函数

前面我们详细介绍了seq2seq的内部的结构，明白了内部结构，想知道是怎么训练的就很容易了。

在上面的图中，我们看到decoder的每一步产生隐状态后，会通过一个projection层映射到对应的词。那怎么去计算每一步的损失呢？实际上，这个projection层，通常是一个softmax神经网络层，假设词汇量是V，则会输出一个V维度的向量，每一维代表是某个词的概率。映射的过程就是把最大概率的那个词找出来作为预测出的词。

在计算损失的时候，我们使用交叉熵作为损失函数，所以我们要找出这个V维向量中，正确预测对应的词的那一维的概率大小 $\large \hat{p}$ ，则这一步的损失就是它的负导数 $\large -log(\hat{p})$ ，将每一步的损失求和，即得到总体的损失函数：

其中T代表Decoder有多少步，[EOS]代表‘end of sentence’也就是<end>这个特殊标记。

Decoding和Beam search

前面画的几个图展示的预测过程，其实就是最简单的decoding方式——「Greedy Decoding」，即每一步，都预测出概率最大的那个词，然后输入给下一步。

这种Greedy的方式，简单快速，但是既然叫“贪心”，肯定会有问题，那就是「每一步最优，不一定全局最优」，这种方式很可能“捡了芝麻，丢了西瓜”。

改进的方法，就是使用「Beam Search」方法：每一步，多选几个作为候选，最后综合考虑，选出最优的组合。

下面我们来具体看看Beam Search的操作步骤：

首先，我们需要设定一个候选集的大小beam size=k；
每一步的开始，我们从每个当前输入对应的所有可能输出，计算每一条路的“序列得分”；
保留“序列得分”最大的k个作为下一步的输入；
不断重复上述过程，直至结束，选择“序列得分”最大的那个序列作为最终结果。

这里的重点就在于这个“序列得分”的计算。

我们使用如下的score函数来定义「序列得分」：

这个score代表了当前到第t步的输出序列的一个综合得分，越高越好。其中 $\large logP(y_i|y_1,y_2,\dots,y_{i-1}, x)$ 类似于前面我们写的第t步的交叉熵损失的负数。所以这个score越到，就意味着到当前这一步为止，输出序列的累积损失越小。

再多描述不如一张图直观，我用下图描绘一个极简的案例（只有3个词的语料，k=2）：

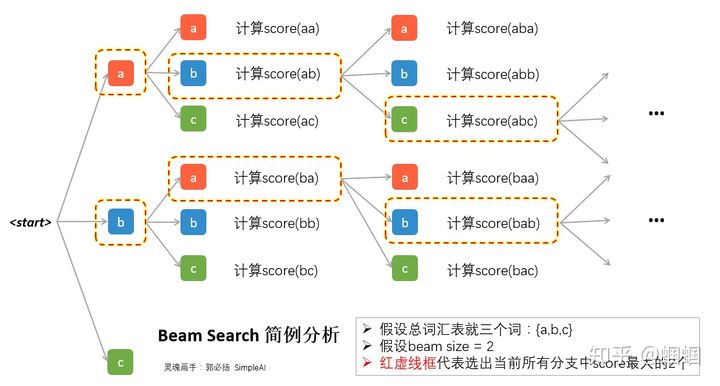
本来想贴CS224N上的图，发现上面省去了一些细节容易造成误解。在每一步，我们都会去对所有的可能输出，计算一次score，假设beam size为k，词汇量为V，那么每一步就需要分出k×V个分支并逐一计算score。所以在图中我们可以看到除了第一步，后面每一步都是分出来2×3=6支。然后综合这k×V个score的结果，只选择其中最大的k个保留。

最后还有一个问题：由于会有多个分支，所以很有可能我们会遇到多个<end>标识，由于分支较多，如果等每一个分支都遇到<end>才停的话，可能耗时太久，因此一般我们会设定一些规则，比如已经走了T步，或者已经积累了N条已完成的句子，就终止beam search过程。

在search结束之后，我们需要对已完成的N个序列做一个抉择，挑选出最好的那个，那不就是通过前面定义的score函数来比较吗？确实可以，但是如果直接使用score来挑选的话，会导致那些很短的句子更容易被选出。因为score函数的每一项都是负的，序列越长，score往往就越小。因此我们可以使用长度来对score函数进行细微的调整：对每个序列的得分，除以序列的长度。根据调整后的结果来选择best one。

Beam Search的使用，往往可以得到比Greedy Search更好的结果，道理很容易理解，高手下棋想三步，深思熟虑才能走得远。