【最优化基础】惩罚和障碍函数

点击【原文】阅读原文，效果更佳！

惩罚和障碍函数

为了简化表示，讨论如下等式约束问题：
$$\begin{array}{rl}\underset{x\text{x}x\in {\mathbb{R}}^n}{\min }& f(x\text{x}x)\\ \text{s.t.}& c(x\text{x}x)=0\text{0}0\end{array}$$
其中，$c(x\text{x}x):{\mathbb{R}}^n\to {\mathbb{R}}^m$，或不等式约束问题
$$\begin{array}{rl}\underset{x\text{x}x\in {\mathbb{R}}^n}{\min }& f(x\text{x}x)\\ \text{s.t.}& c(x\text{x}x)\le 0\text{0}0\end{array}$$

罚函数法

动机

在求解约束不容易消去的非线性规划问题时，为了保证大范围收敛（即从任意的初始近似解都能收敛于一个局部解），必须在"减小目标值"和"保留在可行域内或临近可行域"这两个目标之间进行折衷，这就不可避免地引入了罚函数的思想。

定义

罚函数是目标 $f$ 和约束 $c$ 之间的某种组合，它通过惩罚控项制违反约束来极小化 $f$。

Courant 罚函数

最早的罚函数由 Courant 于 1943 年提出，其采用约束违反量的平方作为惩罚项，因此也称为 Courant 二次罚函数。

例 考虑问题
$$\begin{array}{rl}\min & x\\ \text{s.t.}& 1-x=0\end{array}$$
的罚函数
$$\varphi (x,\sigma )=x+\frac{1}{2}\sigma (1-x{)}^2$$
如下图所示：

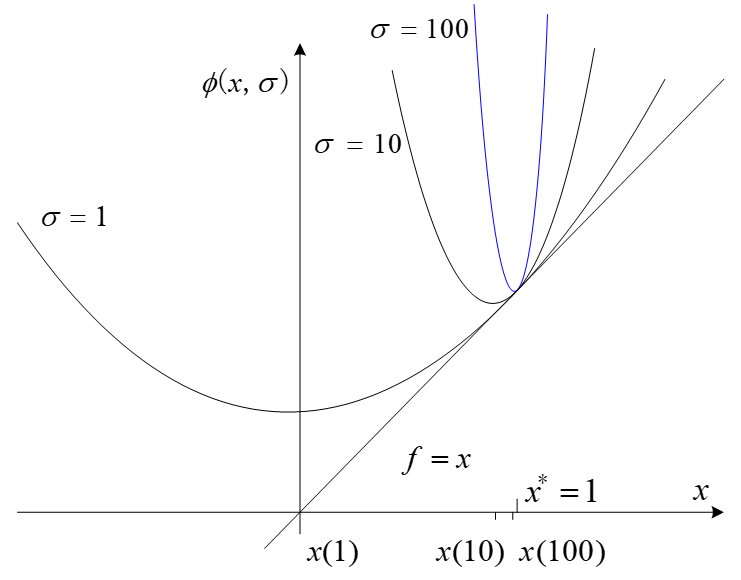
易得当 $\sigma \to \infty$ 时，$\varphi (x,\sigma )$ 的极小点趋近于原问题的最优解 $x^{\ast }=1$。

由此，人们提出了求解一系列极小化问题的技术，成为序列最小化技术。

---

算法 1 序列极小化技术算法

---

• 选择一个固定的序列 { σ i : i = 1 , 2 , 3 , …   } = { 10 , 1 0 2 , 1 0 3 , 1 0 4 , …   } \{\sigma_i : i = 1, 2, 3, \dots\} = \{10,10^2,10^3,10^4,\dots\} {σi​:i=1,2,3,…}={10,102,103,104,…}，使得 ${\sigma }_k\to \infty$；

• do 对于 $\forall {\sigma }_i$，求解
  $$\underset{x\text{x}x}{\min }\varphi (x\text{x}x,{\sigma }_i)$$
  的一个局部最优解 $x\text{x}x({\sigma }_i)$

  while $c(x\text{x}x({\sigma }_i))$ 充分小。

---

事实上，算法 1 不能在有限步内求得全局解，仅是一个理想化的算法。尽管适当放松精度可以保证收敛，但还需假设

• 局部极小点 $x\text{x}x({\sigma }_i)$ 存在；
• 得到的 $x\text{x}x({\sigma }_i)$ 尽可能精确。

在实际应用中，无论是非线性问题无界还是存在局部解，该假设都是不成立的。

定理 1 假设每次得到无约束极小化问题地全局极小点，若 ${\sigma }_k\upharpoonleft \infty$，则

• { ϕ ( x , σ k ) } \{\phi({\pmb x}, \sigma_k)\} {ϕ(xxx,σk​)} 单调递增；
• { c ( k ) T c ( k ) } \{{c^{(k)}}^Tc^{(k)}\} {c(k)Tc(k)} 单调递减；
• { f ( k ) } \{f^{(k)}\} {f(k)} 单调递增，

同时 $c^{(k)}\to 0$，且 { x ( k ) } \{{\pmb x}^{(k)}\} {xxx(k)} 的任何据点是原始问题的解。

证明 略。

注意 结论 2 表明 { x ( k ) } \{{\pmb x}^{(k)}\} {xxx(k)} 是从可行域外接近原问题的解，因此也是外部罚函数。

Lagrange 乘子估计

定义向量 ${\lambda }_i^{(k)}={\sigma }_k{c}_i^{(k)},i=1,2,\dots ,m$ 为 Language 乘子的估计，有如下收敛性性质。

定理 2 假设每次得到无约束问题的局部解，若 ${\sigma }_k\upharpoonleft \infty$，${x\text{x}x}^{\ast }$ 是序列的一个聚点，且 $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}({A\text{A}A}^{\ast })=m$，则 ${x\text{x}x}^{\ast }$ 是原问题的KKT点，有
$$\begin{array}{rlr}{\lambda }^{(k)}& =& {\lambda }^{\ast }+o(1)\\ c^{(k)}& =& \frac{{\lambda }^{\ast }}{{\sigma }_k}+o(\frac{1}{\sigma })\\ {\sigma }_k{c^{(k)}}^T{c}^{(k)}& =& \frac{{{\lambda }^{\ast }}^T{\lambda }^{\ast }}{{\sigma }_k}+o(\frac{1}{\sigma })\end{array}$$
若在 ${x\text{x}x}^{\ast },{\lambda }^{\ast }$ 处二阶充分条件成立，则
$$\begin{array}{rlr}{f}^{\ast }& =& {\varphi }^{\ast }={\varphi }^{(k)}+\frac{1}{2}{\sigma }_k{c^{(k)}}^T{c}^{(k)}+o(\frac{1}{\sigma })\\ h^{(k)}& =& \frac{T^{\ast }{\lambda }^{\ast }}{{\sigma }_k}+o(\frac{1}{\sigma })\end{array}$$
其中，$h^{(k)}={x\text{x}x}^{(k)}-{x\text{x}x}^{\ast }$，$T^{\ast }$ 定义为

$$\left[\begin{array}{cc}{W}^{\ast }& A^{\ast }\\ {A^{\ast }}^T& 0\end{array}\right]=\left[\begin{array}{cc}{H}^{\ast }& T^{\ast }\\ {T^{\ast }}^T& U^{\ast }\end{array}\right]$$

---

事实上，对于二次罚函数，有
$${\nabla }^2\varphi ({x\text{x}x}^{(k)},{\sigma }_k)=W^{(k)}+{\sigma }_k{A}^{(k)}{A^{(k)}}^T$$
其中，$W^{(k)}={\nabla }_{x\text{x}x}^2\mathcal{L}({x\text{x}x}^{(k)},{\lambda }^{(k)})$，${\lambda }_i^{(k)}={\sigma }_k{c}_i^{(k)},i=1,2,\dots ,m$。其特点是一阶可微，但需要满足 ${\sigma }_k\to \infty$。

不等式约束罚函数

不等式约束问题，可以等价地转化为等式约束
c ( x ) ≤ 0    ⟺    max ⁡ { c ( x ) , 0 } = 0 c({\pmb x}) \leq 0 \iff \max\{c({\pmb x}),0\} = 0 c(xxx)≤0⟺max{c(xxx),0}=0
从而，不等式约束问题地罚函数为
ϕ ( x , σ ) = f ( x ) + 1 2 σ ∑ i ∈ I max ⁡ { c i ( x ) , 0 } \phi({\pmb x}, \sigma) = f({\pmb x}) + \frac{1}{2}\sigma\sum_{i \in \mathcal{I}} \max\{c_i({\pmb x}),0\} ϕ(xxx,σ)=f(xxx)+21​σi∈I∑​max{ci​(xxx),0}

障碍函数

由于该方法适合可行域外无定义的约束问题，因为得到的序列极小化问题也是可行的，因此该方法也被成为内点法。

定义

障碍函数法是一种求解不等式约束问题的序列极小化方法，其旨在障碍项在边界上取值为无穷大，从而在任何时候都能满足约束。

对数障碍函数

1955 年，Frisch 提出对数障碍函数
$$\varphi (x\text{x}x,\mu )=f(x\text{x}x)-\mu \sum _i\log (-c_i(x\text{x}x))$$
例 对于不等式约束问题
$$\begin{array}{rl}\min & x\\ \text{s.t.}& 1-x\le 0\end{array}$$
其对数障碍函数 $\varphi (x,\mu )=x-\mu \log (x-1)$ 图像如下，可以看出当 ${\mu }_k\to 0$ 时，$x({\mu }_k)\to x^{\ast }$。

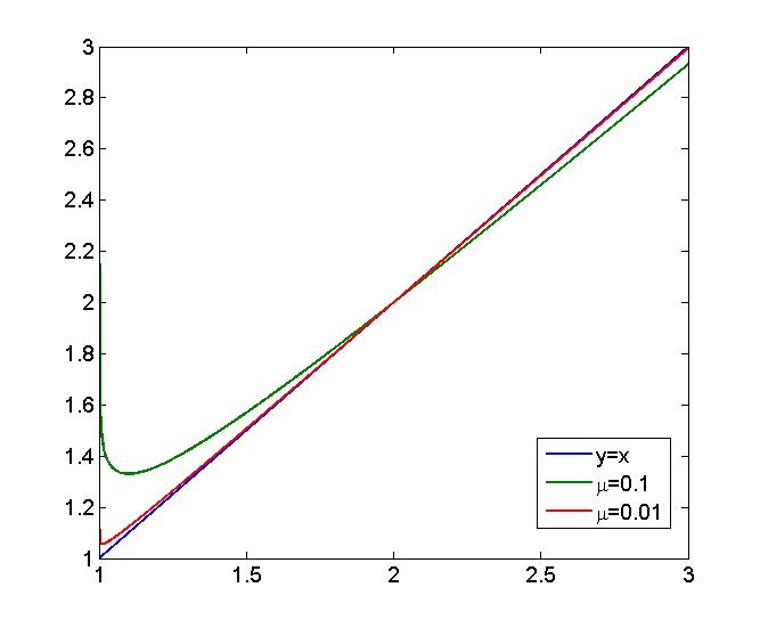
特点：原问题是凸规划时，障碍函数时凸函数。一阶可微，需要满足 $\mu \to 0$。

倒数障碍函数

1961 年，Carroll 提出倒数障碍函数
$$\varphi (x\text{x}x,\mu )=f(x\text{x}x)-\mu \sum _{i=1}^m[c_i(x\text{x}x){]}^{-1}$$
一般来说，倒数障碍函数比二次罚函数和对数障碍函数要差。

内点法（路径跟踪法）

对数障碍函数法也称为原始内点法，其中乘子由原始变量确定。

令 $C(x)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(c_1(x),c_2(x),\cdots ,c_m(x))$，$A(x)=[a_1(x),a_2(x),\dots ,a_m(x)]$，则

KKT 条件

$$\begin{array}{rlr}g(x)+A(x)\lambda & =& 0\\ C(x)\lambda & =& 0\\ c(x)& \le & 0\\ \lambda & \ge & 0\end{array}$$

扰动的 KKT 条件

$$\begin{array}{rlr}g(x)+A(x)\lambda & =& 0\\ C(x)\lambda & =& -\mu \\ c(x)& <& 0\\ \lambda & >& 0\end{array}$$

动机

令 $\mu \to 0$，跟踪方程组
$$\begin{array}{rlr}g(x)+A(x)\lambda & =& 0\\ C(x)+\mu & =& 0\end{array}$$
保存 $c(x)<0,\lambda >0$ 的解，直至 $\mu$ 逐渐递减至零。

参考资料

[1] 刘红英，夏勇，周永生. 数学规划基础，北京，北京航空航天大学出版社，2012.