【最优化】序列（逐步）二次规划法（SQP）

序列（逐步）二次规划法（SQP）

一种直接有效求解非线性约束问题的方法是基于问题中的函数 $f(x)$ 和 $c_i(x)$ 的某种近似迭代法，尤其是利用约束函数 $c_i(x)$ 的线性近似。基于这种思想的一个方法是利用 Newton 法求解 Lagrange 函数的稳定点，因此也被称为 Lagrange-Newton 法。

等式约束问题—— KKT 条件解方程

例 考虑非线性规划问题
$$\begin{array}{rl}\min & x_1+x_2\\ \mathrm{s}.\mathrm{t}.& x_1^2=x_2\end{array}$$

• 解析法求解

构造 Lagrange 函数
$$\mathcal{L}=x_1+x_2+\lambda (x_1^2-x_2)$$
其 KKT 条件为
$$\begin{array}{rl}1+2\lambda x_1& =0\\ 1-\lambda & =0\\ x_1^2-x_2& =0\end{array}$$
解析法求得 $x^{\ast }=(-\frac{1}{2},\frac{1}{4})$，${\lambda }^{\ast }=1$。

• 以 $x^{(0)}=(0,0)$，${\lambda }^{(0)}$ 为初始点，用数值方法求 KKT 点

出发点：解方程组的 Newton 法，线性近似的思想

设 $\varphi (t):\mathbb{R}\to \mathbb{R}$，求 $\varphi (t)$ 的根，即解方程组 $\varphi (t)=0$。

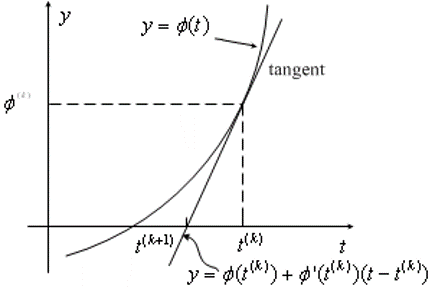
等式约束问题——解方程组的 Newton 法

设 $z\in {\mathbb{R}}^n$，解方程组
$$\begin{array}{rl}{r}_1(z)& =0\\ r_2(z)& =0\\ ⋮& \\ r_n(z)& =0\end{array}$$
给定近似解 $z^{(k)}$，令 $s^{(k)}=z^{(k+1)}-z^{(k)}$
$$r^{(k)}=\left[\begin{array}{c}{r}_1(z^{(k)})\\ r_2(z^{(k)})\\ ⋮\\ r_n(z^{(k)})\end{array}\right]$$

$$J(z^{(k)})=\left[\begin{array}{c}\nabla r_1(z^{(k)}{)}^T\\ \nabla r_2(z^{(k)}{)}^T\\ ⋮\\ \nabla r_n(z^{(k)}{)}^T\end{array}\right]$$

形成冰求解线性方程组
$$\begin{array}{rl}{l}_1(s)& :=r_1(z^{(k)})+\nabla r_1(z^{(k)}{)}^{T}s=0\\ l_2(s)& :=r_2(z^{(k)})+\nabla r_2(z^{(k)}{)}^{T}s=0\\ ⋮& \\ l_n(s)& :=r_n(z^{(k)})+\nabla r_n(z^{(k)}{)}^{T}s=0\end{array}$$
即
$$J(z^{(k)})s=-r^{(k)}$$

实用方法会加上线搜索或信赖域技术确保方法是大范围收敛的！

等式约束问题—— Lagrange-Newton 法

考虑等式约束问题
$$\begin{array}{rl}\underset{x\in {\mathbb{R}}^n}{\min }& f(x)\\ \mathrm{s}.\mathrm{t}.& c_i(x)=0,i=1,2,\cdots ,m\end{array}$$
即
$$\begin{array}{rl}\underset{x\in {\mathbb{R}}^n}{\min }& f(x)\\ \mathrm{s}.\mathrm{t}.& c(x)=0\end{array}$$
其中，$c(x):{\mathbb{R}}^n\to {\mathbb{R}}^m$。

KKT 条件为
$$\begin{array}{rl}g(x)+A(x)\lambda & =0\\ c(x)& =0\end{array}$$
其中，$A(x)=[\nabla c_1(x),\nabla c_2(x),\cdots ,\nabla c_m(x)]$。

设 $(x^{(k)},{\lambda }^{(k)})$ 是近似解，则其牛顿校正 $(s^{(k)},w^{(k)})$满足
$$\left[\begin{array}{cc}{W}^{(k)}& A^{(k)}\\ {A^{(k)}}^T& 0\end{array}\right]\left[\begin{array}{c}s\\ w\end{array}\right]=-\left[\begin{array}{c}{g}^{(k)}+A^{(k)}\lambda \\ c^{(k)}\end{array}\right]$$
其中，$A^{(k)}=A(x^{(k)})$，$W^{(k)}={\nabla }^{2}f(x^{(k)})+{\sum }_i{\lambda }_i^{(k)}{\nabla }^2{c}_i(x^{(k)})$

令 ${\lambda }^{(k+1)}={\lambda }^{(k)}+w^{(k)}$，则 $(s^{(k)},{\lambda }^{(k+1)})$ 满足
$$\left[\begin{array}{cc}{W}^{(k)}& A^{(k)}\\ {A^{(k)}}^T& 0\end{array}\right]\left[\begin{array}{c}s\\ \lambda \end{array}\right]=-\left[\begin{array}{c}{g}^{(k)}\\ c^{(k)}\end{array}\right]$$
给定初始点 $(x^{(0)},{\lambda }^{(0)})$，构造并求解线性方程组得 $(s^{(k)},{\lambda }^{(k+1)})$，令 $x^{(k+1)}=x^{(k)}+s^{(k)}$，依次重复。

Lagrange 乘子法 + Newton 法 = Lagrange-Newton 法

性质

定理 假设 $(x^{\ast },{\lambda }^{\ast })$ 满足等式约束问题得二阶充分条件，且 $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(A^{\ast })=m$，则当 $x^{(0)}$ 充分接近 $x^{\ast }$ 且 ${\lambda }^{(0)}$ 使得矩阵
$$\left[\begin{array}{cc}{W}^{(0)}& A^{(0)}\\ {A^{(0)}}^T& 0\end{array}\right]$$
非奇异，则 Lagrange-Newton 法有定义，且由该方法产生得序列 { ( x ( k ) , λ ( k ) } \{(x^{(k)},\lambda^{(k)}\} {(x(k),λ(k)} 二次收敛于 $(x^{\ast },{\lambda }^{\ast })$。

存在的问题

• 对初始点要求高
• 需要求二阶导数
• 不能求解含不等式约束的优化问题

基本/局部 SQP

动机

考虑二次规划子问题
$$\begin{array}{rl}\underset{s\in {\mathbb{R}}^n}{\min }& \frac{1}{2}{s}^T{W}^{(k)}s+{g^{(k)}}^{T}s+f^{(k)}\\ \mathrm{s}.\mathrm{t}.& {A^{(k)}}^{T}s+c^{(k)}=0\end{array}$$
其中，$s=x-x^{(k)}$，目标函数是修正了二次项的二阶 Taylor 展式。其一阶（KKT）条件是
$$\begin{array}{rl}{W}^{(k)}s+g^{(k)}+A^{(k)}\lambda & =0\\ {A^{(k)}}^{T}s+c^{(k)}& =0\end{array}$$
改写成块矩阵形式如下：
$$\left[\begin{array}{cc}{W}^{(k)}& A^{(k)}\\ {A^{(k)}}^T& 0\end{array}\right]\left[\begin{array}{c}s\\ \lambda \end{array}\right]=-\left[\begin{array}{c}{g}^{(k)}\\ c^{(k)}\end{array}\right]$$

设 $Z^{(k)}\in {\mathbb{R}}^{n\times (n-m)}$ 的列生成 ${A^{(k)}}^{T}s=0$ 的解空间，若 $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(A^{(k)})=m$，且 $Z^{(k)}{W}^{(k)}{Z}^{(k)}$ 正定，则原问题与一阶条件的解相同，且解唯一。

对于一般的非线性规划问题
$$\begin{array}{rl}\underset{s\in {\mathbb{R}}^n}{\min }& \frac{1}{2}{s}^T{W}^{(k)}s+{g^{(k)}}^{T}s+f^{(k)}\\ \mathrm{s}.\mathrm{t}.& {a_i^{(k)}}^{T}s+c_i^{(k)}=0,i\in \mathcal{E}\\ & {a_i^{(k)}}^{T}s+c_i^{(k)}=0,i\in \mathcal{I}\end{array}$$
有如下求解算法：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-s4TnoKaq-1610379805928)(https://cdn.jsdelivr.net/gh/ZhouKanglei/jidianxia/2020-12-24/1608821899495-SQP.png)]

理想的终止条件：满足 KKT 条件！

例 考虑非线性规划问题
$$\begin{array}{rl}\min & f(x)=-x_1-x_2\\ \mathrm{s}.\mathrm{t}.& c_1(x)=x_1^2-x_2\le 0\\ & c_2(x)=x_1^2+x_2^2-1\le 0\end{array}$$
其几何直观如下：

解析法求得其最优解 $x^{\ast }=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}{)}^T$，${\lambda }^{\ast }=(0,\frac{1}{\sqrt{2}}{)}^T$。

给定初始点 $x^{(0)}=(\frac{1}{2},1{)}^T$，${\lambda }^{(0)}=(0,0{)}^T$，其迭代步骤如下：

优点

局部二阶收敛

存在问题

• 初始点不好时，迭代可能发散
• 子问题的解可能不存在，比如无界或者不可行
• 需要二阶偏导数 $W^{(k)}$

参考资料

[1] 刘红英，夏勇，周永生. 数学规划基础，北京，北京航空航天大学出版社，2012.