贝叶斯估计
假设我们有样本D={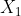 ~
~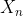 },并且已知x~
},并且已知x~ 其中
其中 未知,
未知,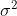 已知,又已知
已知,又已知 ~
~ .
.
 ,其中
,其中 表示在给定的样本条件
表示在给定的样本条件
下来估计x的概率密度。我们需要求 和
和 .
.
首先 ,其中
,其中
 ,其中
,其中

 ,(其中
,(其中 )。
)。
 ,
, 前面的系数相等则有:
前面的系数相等则有: ,
,
 ,
, ,所以
,所以 ~
~ ,可以看出当n趋于无穷大的时候:
,可以看出当n趋于无穷大的时候:
 ,当n趋于无穷大时贝叶斯估计等于最大似然估计。
,当n趋于无穷大时贝叶斯估计等于最大似然估计。
令 ,因为该积分只与
,因为该积分只与 有关。
有关。
上式继续化简: ,解得
,解得 ~
~ .
.
总结:
当上式中整个积分不好求的时候,我们可以求最大后验估计:
 ,这样计算比较容易。
,这样计算比较容易。
如果 没有已知的先验分布的话,即先验分布是扁平的,就是上式中
没有已知的先验分布的话,即先验分布是扁平的,就是上式中 不变,
不变,
那么最大后验估计等于最大似然估计
我们再来看一下:
 ,其中
,其中 ,
,
m是样本均值,上式可以看出贝叶斯估计是样本均值和先验均值 的加权平均。
的加权平均。
并且m和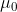 哪一个方差小,哪一个占的比重就大。
哪一个方差小,哪一个占的比重就大。
当n趋于无穷大时贝叶斯估计更逼近样本均值。
当先验的方差 较小时,即关于先验概率的不确定性较少时,或者样本数n较小时,
较小时,即关于先验概率的不确定性较少时,或者样本数n较小时,
贝叶斯估计更加依赖先验均值。





















 5519
5519











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








