等值线追踪算法
前篇提到了一种直接绘制等值线的方法,但是那种方法没办法确定每一条线上的点。如果我们想给等值线限定一些条件,如太短不绘制,标定等值线值等,上一种方法则无法使用。因此我又写了一个等值线的追踪算法。
等值线追踪算法
等值线追踪算法,顾名思义,就是把每条线上的点,按顺序追踪出来,这样直接按照顺序绘制便能绘制出完整的线段。
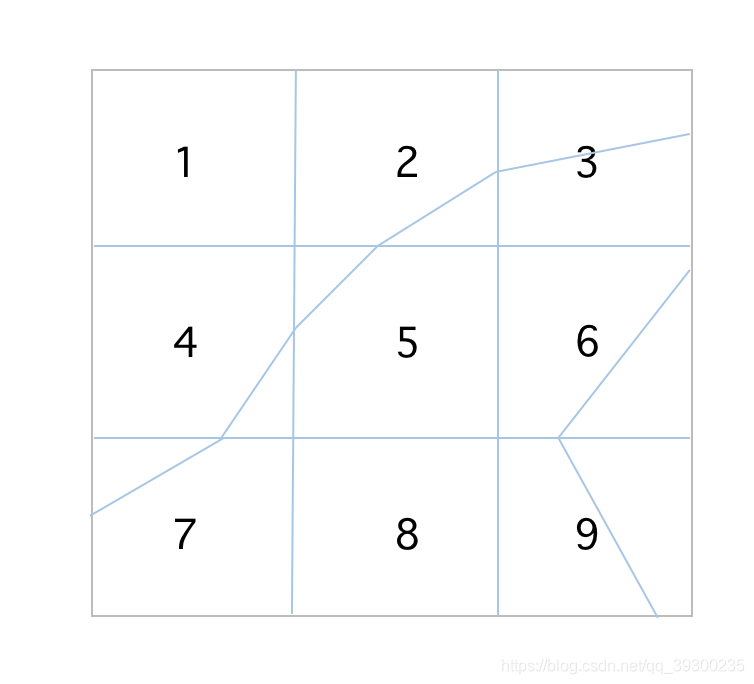
如图5号网格,要确定哪个线段是接下来要连接的线段,则需要遍历周围的网格确定线条。我们便可以发现2,4号网格内的线条是需要的线条,而六号网格内的则不是。我们如何确定周围网格里的线条是否是接下来要连接的线条呢。
我们曾今在等值线绘制算法中记录了一个线表:
//矩形4位2进制对应连接线,连接线对应两个边(索引)上的点。
const unsigned char lineTable[16][5]={
{255,255,255,255,255},
{4,1,255,255,255},
{2,1,255,255,255},
{4,2,255,255,255},
{3,2,255,255,255},
{4,3,2,1,255},
{3,1,255,255,255},
{4,3,255,255,255},
{4,3,255,255,255},
{3,1,255,255,255},
{3,2,1,4,255},
{3,2,255,255,255},
{4,2,255,255,255},
{2,1,255,255,255},
{4,1,255,255,255},
{255,255,255,255,255}
};该表格记录了一个网格中所有线条可能的情况,因此根据该表在5号网格的情况下一个查找网格就变成2号和4号网格。由于5号网格内的顶点索引为0001,转换为10进制为1,对应lineTable[1]内为4,1。证明点落在4号边和1号边上,我们4号边则查找x-1的网格,1号边则找y-1的网格(左上角为原点)。

如图所示,我们查完线表之后,观察边编号,便可以直接获得接下来需要查找的网格,省去了对周围每个网格的遍历。我们发现1对3,2对4,3对1,4对2。因此可以同样建立表:const unsigned char posTable[5]={0,3,4,1,2};帮助我们获取接下来的网格点在哪个边上。
等值线追踪算法步骤
和等值线绘制算法相同,我们首先建立网格。然后遍历所有网格,当在网格中发现有线存在,则根据上述追踪规则重复追踪迭代,我们用一个bool的2维数组m_bTrick保存该网格是否查找过(初始化为1),每次遍历或者迭代完成时,令bool置0。这时我们发现会有一种特殊情况,就是一个网格中有可能出现2条线,如线表中第5种和第10种情况。因此我们只能将bool改为int,让每次迭代时,若m_bTrick为1,则判断是否有可能为2条边,如果为两条边则置为2,否则置为0。当下次查找到该网格m_bTrick为2时,则直接置为0即可。由于我们需要完整的查找出完整的线段,因此我们需要双向迭代,如图1中5号网格,我们首先按照边编号4方向迭代完所有的线,然后按照边编号1方向迭代,最后连接两个方向迭代的线,就是最后我们需要的等值线了。

按照该算法,图一的结果为上图所示:黑色编号为网格编号,红色编号为程序执行顺序。我们首先遍历到1号网格,发现无线,则置m_bTrick为0,然后查找2号网格,发现其中有线条,取出线条的两个端点边编号4和2,先从边编号4进行迭代,查找到5号网格,同理再是4号,7号。完成之后2号网格的边编号4方向已经迭代完成,然后从边编号2方向迭代到网格3,网格3之后该线便完成迭代,我们继续遍历,遍历到网格4,5发现m_bTrick为0。因此到网格6才发现线条,在迭代到网格9。所以8号网格成为了最后访问的网格。
追踪代码
我们的追踪代码可以直接加入我们的等值线绘制代码中。
我们增加代码:
struct Dpos{//迭代中用于返回xy值
Dpos(){l=0;r=0;n=0;}
unsigned int l,r;
bool n;//是否有线
};
//等值线值为isoL时的所有线
struct ClineIsoLevel{
float isoL;
vector<vector<unsigned int>> isoLines;
};
typedef std::vector<ClineIsoLevel> CtLineTrack;
class Contour_line{
public:
......
//追踪生成等值线
bool CreatLineTra(float* field,int n[2],vector<float> threshold,vector<float> &vrts,
CtLineTrack& lns);
//从标量场追踪等值线
void TrackLineV(vector<float> &vrts,CtLineTrack& lns);
private:
......
vector<int> m_bTrick;//判断网格上还有几条线
ClineIsoLevel m_allIsoLines;//记录每一个等值线阈值上的点
//追踪递归
Dpos TrackRecursive(unsigned int x,unsigned int y,unsigned int iso,unsigned int edge);
// c输出追踪出的等值线点信息和线信息
void RenameTrackVerticesAndLines(vector<float> &vrts, unsigned int &nvrts,
CtLineTrack& lns);
}实现代码如下:
bool Contour_line::CreatLineTra(float* field,int n[2],vector<float> threshold,vector<float> &vrts,
CtLineTrack& lns){
if (field==nullptr) return false;
m_sliceX=n[0];
m_Grid[0]=(n[0]-1)/m_stride;
m_Grid[1]=(n[1]-1)/m_stride;
m_tIsoLevel=threshold;
m_ptScalarField=field;
TrackLineV(vrts,lns);//追踪算法
return true;
}
/* 等值线信息生成(等值线追踪的迭代方式)
* @param [out] vrts等值线顶点
* @param [out] lns等值线信息(顶点连接信息)
*/
void Contour_line::TrackLineV(vector<float> &vrts,CtLineTrack& lns){
if (m_bValidLine)
DeleteLine();
//等值线生成
for (unsigned int iso=0; iso<m_tIsoLevel.size(); iso++) {
ClineIsoLevel currentIsoL;//每次保存该值的所有等值线
currentIsoL.isoL=m_tIsoLevel[iso];
m_bTrick.clear();
m_bTrick.resize(m_Grid[0]*m_Grid[1], 1);//每次更新表格初始化为1
for (unsigned int y=0; y<m_Grid[1]; y++) {
for (unsigned int x=0; x<m_Grid[0]; x++) {
if (m_bTrick[y*m_Grid[0]+x]) {
vector<unsigned int>currentL,currentR;//保存其中一条
unsigned int nx=x,ny=y,lastL,lastR;
Dpos np=TrackRecursive(nx,ny,iso,0),fp=np;
if (np.n) {
lastL=np.l;
lastR=np.r;
while (np.n) {//处理左边线
unsigned int id;
switch (lastL) {//查表判断下一个网格遍历位置
case 1:
id=GetEdgeID(nx, ny, 1);
np=TrackRecursive(nx, ny-=1, iso,posTable[1]);
break;
case 2:
id=GetEdgeID(nx, ny, 2);
np=TrackRecursive(nx+=1, ny, iso,posTable[2]);
break;
case 3:
id=GetEdgeID(nx, ny, 3);
np=TrackRecursive(nx, ny+=1, iso,posTable[3]);
break;
case 4:
id=GetEdgeID(nx, ny, 4);
np=TrackRecursive(nx-=1, ny, iso,posTable[4]);
break;
}
currentL.push_back(id);
lastL=np.r;
}
np=fp; nx=x;ny=y;
while (np.n) {//处理右边线
unsigned int id;
switch (lastR) {
case 1:
id=GetEdgeID(nx, ny, 1);
np=TrackRecursive(nx, ny-=1, iso,posTable[1]);
break;
case 2:
id=GetEdgeID(nx, ny, 2);
np=TrackRecursive(nx+=1, ny, iso,posTable[2]);
break;
case 3:
id=GetEdgeID(nx, ny, 3);
np=TrackRecursive(nx, ny+=1, iso,posTable[3]);
break;
case 4:
id=GetEdgeID(nx, ny, 4);
np=TrackRecursive(nx-=1, ny, iso,posTable[4]);
break;
}
currentR.push_back(id);
lastR=np.r;
}
for (int i=0; i<(currentR.size()+1)/2; i++) {
unsigned int temp=currentR[i];
currentR[i]=currentR[currentR.size()-i-1];
currentR[currentR.size()-i-1]=temp;
}
for (int i=0; i<currentL.size(); i++) {
currentR.push_back(currentL[i]);
}
currentIsoL.isoLines.push_back(currentR);
}
}
}
}
m_allIsoLines=currentIsoL;
RenameTrackVerticesAndLines(vrts, m_nVertices, lns);
}
m_bValidLine=true;
}
/* 追踪算法
* @param [out] vrts等值线顶点
* @param [out] lns等值线信息(顶点连接信息)
*/
Dpos Contour_line::TrackRecursive(unsigned int x,unsigned int y,unsigned int iso,unsigned int edge){
Dpos apos;
if (x<m_Grid[0]&&y<m_Grid[1]&&m_bTrick[y*m_Grid[0]+x]) {
//计算网格内的顶点放置信息索引
unsigned int tableIndex=0;
int stx=m_stride*x,sty=m_stride*y;
//存在空值情况
int nanCount=0,nanNum=0;
if (m_ptScalarField[6*(sty*m_sliceX+stx)+2]==-1.0){
nanCount++;
nanNum=1;
}
else if (m_ptScalarField[6*(sty*m_sliceX+stx)+2]<m_tIsoLevel[iso])
tableIndex|=1;
if (m_ptScalarField[6*(sty*m_sliceX+stx+m_stride)+2]==-1.0){
nanCount++;
nanNum=2;
}
else if (m_ptScalarField[6*(sty*m_sliceX+stx+m_stride)+2]<m_tIsoLevel[iso])
tableIndex|=2;
if (m_ptScalarField[6*((sty+m_stride)*m_sliceX+stx+m_stride)+2]==-1.0){
nanCount++;
nanNum=3;
}
else if(m_ptScalarField[6*((sty+m_stride)*m_sliceX+stx+m_stride)+2]<m_tIsoLevel[iso])
tableIndex|=4;
if (m_ptScalarField[6*((sty+m_stride)*m_sliceX+stx)+2]==-1.0){
nanCount++;
nanNum=4;
}
else if (m_ptScalarField[6*((sty+m_stride)*m_sliceX+stx)+2]<m_tIsoLevel[iso])
tableIndex|=8;
//处理单nan特殊情况
if (nanCount==1) {
int mid=pow(2, nanNum-1);
int left=(nanNum-1)<1?4:(nanNum-1);
left=pow(2, left-1);
int right=(nanNum+1)>4?1:(nanNum+1);
right=pow(2, right-1);
if ((tableIndex&left)==(tableIndex&right)) {
tableIndex|=(tableIndex&left)∣
nanCount=0;
}
}
if (edgeTable[tableIndex]!=0) {
//计算边上的顶点
if (edgeTable[tableIndex]&1) {
CtVertexID pt=CalculateIntersection(stx, sty, 1,iso);
unsigned int id=GetEdgeID(x, y, 1);
m_i2v.insert(ID2VertexID::value_type(id,pt));
}
if (edgeTable[tableIndex]&8) {
CtVertexID pt=CalculateIntersection(stx, sty, 4,iso);
unsigned int id=GetEdgeID(x, y, 4);
m_i2v.insert(ID2VertexID::value_type(id,pt));
}
if(x==m_Grid[0]-1){
if (edgeTable[tableIndex]&2) {
CtVertexID pt=CalculateIntersection(stx, sty, 2,iso);
unsigned int id=GetEdgeID(x, y, 2);
m_i2v.insert(ID2VertexID::value_type(id,pt));
}
}
if(y==m_Grid[1]-1){
if (edgeTable[tableIndex]&4) {
CtVertexID pt=CalculateIntersection(stx, sty, 3,iso);
unsigned int id=GetEdgeID(x, y, 3);
m_i2v.insert(ID2VertexID::value_type(id,pt));
}
}
if (!nanCount) {
//生成等值线,获取线上的点在哪条边上
apos.n=1;
if(edge!=0){//当非第一次遍历时在r中存放接下来的点
for (unsigned int i=0; lineTable[tableIndex][i]!=255; i+=2) {
unsigned int pointID1,pointID2;
pointID1=lineTable[tableIndex][i];
pointID2=lineTable[tableIndex][i+1];
if (pointID1==edge)
apos.r=pointID2;//用r表示下个点
else if(pointID2==edge)
apos.r=pointID1;
}
}else{
apos.l=lineTable[tableIndex][0];
apos.r=lineTable[tableIndex][1];
}
if(lineTable[tableIndex][2]!=255){//处理一个网格有两条线情况,0,1,2三个值
if (m_bTrick[y*m_Grid[0]+x]==1)
m_bTrick[y*m_Grid[0]+x]=2;
else
m_bTrick[y*m_Grid[0]+x]=0;
}
else
m_bTrick[y*m_Grid[0]+x]=0;
return apos;
}
}
m_bTrick[y*m_Grid[0]+x]=0;
}
apos.n=0;
return apos;
}
/*!
* 复制信息到顶点和线缓存中
* @param [out] vrts顶点坐标
* @param [out] nvrts顶点数
* @param [out] lns等值线的几何信息
*/
void Contour_line::RenameTrackVerticesAndLines(vector<float> &vrts, unsigned int &nvrts,
CtLineTrack& lns){
static unsigned int nextID=0;
auto mapIt=m_i2v.begin();
//为每个顶点标记在顶点缓存中的编号
while (mapIt!=m_i2v.end()) {
(*mapIt).second.newID=nextID;
nextID++;
mapIt++;
}
//将等值线m_allIsoLines内的顶点编号更新为顶点缓存中的编号
for (int j=0; j<m_allIsoLines.isoLines.size(); j++) {//每个阈值下的每条等值线
for (int k=0; k<m_allIsoLines.isoLines[j].size(); k++) {//每条等值线上的点
unsigned int newID=m_i2v[m_allIsoLines.isoLines[j][k]].newID;
m_allIsoLines.isoLines[j][k]=newID;
}
}
//复制所有的顶点到顶点缓存vrts中
mapIt=m_i2v.begin();
nvrts=int(m_i2v.size());
for (unsigned int i=0; i<nvrts; i++,mapIt++) {
vrts.push_back((*mapIt).second.x);
vrts.push_back((*mapIt).second.y);
}
lns.push_back(m_allIsoLines);
//释放空间
m_i2v.clear();
m_lineVertex.clear();
}
我们实现的效果图如下:

由于追踪出的线条可以做一些筛选操作,因此我们的效果可以比直接绘制的等值线好很多。























 9357
9357

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








