光线跟踪的几种常见求交运算

最新推荐文章于 2024-04-04 22:49:54 发布

0小龙虾0

最新推荐文章于 2024-04-04 22:49:54 发布

阅读量5.1k

点赞数 18

光线跟踪的几种常见求交运算

我们知道光线跟踪中最昂贵的就是和几何对象的求交运算了。这里就记录几个比较常见的光线和几何对象求交运算。

球

射线与球体相交可能是射线几何相交测试的最简单形式，这就是为什么这么多射线追踪器显示球体图像的原因。由于其简单性，它还具有非常快的优势。可以使用两种方法实施此测试。第一个使用几何来解决问题。第二种技术是我们最常用的方法，我们称它为代数法。这都是我们初中的知识点了。

几何法：

射线-球面相交测试的几何解决方案依赖于简单的三角学。如下图：

我们要找到射线与球体相交的点，即点P和P'的位置，我们需要找到t0和t1的值。我们可以使用以下参数形式来表示射线：

其中O代表射线的起点，D代表射线的方向（通常是单位化的）。更改t的值可以定义沿射线的任何位置。通过观察上图，可以发现通过从 $t_{ca}$ 中减去 $t_{hc}$ 来得到到t0，并且可以通过将此时间 $t_{ca}$ 加到 $t_{hc}$ 来找到t1。我们需要做的就是找到计算这两个值（ $t_{hc}$ 和 $t_{ca}$ ）的方法，从中我们可以得到t0，t1，然后使用射线公式：

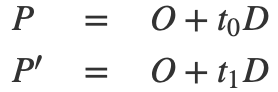
来计算出P和P'。由于D是单位向量，我们可以得到：

我再计算d，通过公式：

获得d之后，我们可以计算出 $t_{hc}$ 值，然后和之前获得的 $t_{ca}$ 来计算出t0，t1：

代数法：

代数法中，利用球体公式：

当我们的射线若和球有交点，则有：

该函数也正是我们CG中常说的隐函数。其构成的形状可以称为隐式形状。提一下：隐式形状为不能根据相互连接的多边形定义的形状，而是仅根据方程式定义的形状。

我们用射线公式带入P，有：

左边有：

我们利用公式：

当 $f(x)=0$ 的时候，有：

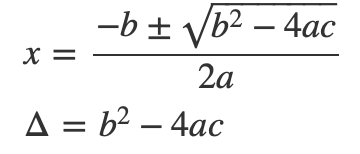
这时则可以根据 $\triangle$ 来判断交点个数。当 $\triangle$ =0时，只有一个交点。当 $\triangle$ <0时，没有交点。当 $\triangle$ >0时，有2个交点。这里贴出我们的代码：

bool solveQuadratic(const float &a, const float &b, const float &c, float &x0, float &x1) 
{ 
    float discr = b * b - 4 * a * c; 
    if (discr < 0) return false; 
    else if (discr == 0) x0 = x1 = - 0.5 * b / a; 
    else { 
        float q = (b > 0) ? 
            -0.5 * (b + sqrt(discr)) : 
            -0.5 * (b - sqrt(discr)); 
        x0 = q / a; 
        x1 = c / q; 
    } 
    if (x0 > x1) std::swap(x0, x1); 
 
    return true; 
} 

bool intersect(const Ray &ray) const 
{ 
        float t0, t1; // 交点t 
#if 0 
        // 几何解法
        Vec3f L = center - orig; 
        float tca = L.dotProduct(dir); 
        // if (tca < 0) return false;
        float d2 = L.dotProduct(L) - tca * tca; 
        if (d2 > radius2) return false; 
        float thc = sqrt(radius2 - d2); 
        t0 = tca - thc; 
        t1 = tca + thc; 
#else 
        // 代数解法
        Vec3f L = orig - center; 
        float a = dir.dotProduct(dir); 
        float b = 2 * dir.dotProduct(L); 
        float c = L.dotProduct(L) - radius2; 
        if (!solveQuadratic(a, b, c, t0, t1)) return false; 
#endif 
        if (t0 > t1) std::swap(t0, t1); 
 
        if (t0 < 0) { 
            t0 = t1; // 如果t0小于0用t1代替
            if (t0 < 0) return false; // 如果t0，t1都为负数，则返回false
        } 
 
        t = t0; //返回近的点
 
        return true; 
}

平面

平面和射线的求交也非常简单，我们看下图：

若我们击中点为p，有：

其中n为平面的法线。我们射线的公示都是一致的：

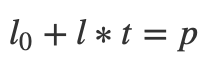
为了和圆求交做区分，我们将起始点设为 $l_{0}$ ，方向为 $l$ 。带入公式中有：

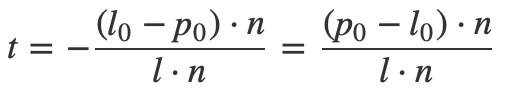
我们的代码为：

bool intersectPlane(const Vec3f &n, const Vec3f &p0, const Vec3f &l0, const Vec3f &l, float &t) 
{ 
    //向量都为单位化的
    float denom = dotProduct(n, l); 
    if (denom > 1e-6) { 
        Vec3f p0l0 = p0 - l0; 
        t = dotProduct(p0l0, n) / denom; 
        return (t >= 0); 
    } 
 
    return false; 
}

那么若要计算射线和圆盘的交点，则只需要多判断是否落入圆盘半径内，如下图：

我们这里就直接贴代码：

bool intersectDisk(const Vec3f &n, const Vec3f &p0, const float &radius, const Vec3f &l0, const Vec3 &l) 
{ 
    float t = 0; 
    if (intersectPlane(n, p0, l0, l, t)) { 
        Vec3f p = l0 + l * t; 
        Vec3f v = p - p0; 
        float d2 = dot(v, v); 
        return (sqrtf(d2) <= radius); 
     } 
 
     return false; 
}

盒子(BOX)

我们的盒子有两种，一种是边框与坐标轴对齐的轴对齐边界框(简称AABB)，另一种是不与坐标轴对齐的定向边界框(简称OBB)。计算和AABB求交时，我们的BOX可以有一下定义：

class Box3 
{ 
public: 
    Box3(cont Vec3f &vmin, const Vec3f &vmax) 
    { 
        bounds[0] = vmin; 
        bounds[1] = vmax; 
    } 
    Vec3f bounds[2]; 
};

BOX中只有两个对象，一个是盒子的左下角坐标，另一个是右上角坐标。我们许多仿真模拟的均匀网格法都可以用这个BOX来定义网格。

我们设B0x的值为bounds[0].x。则x=B0x代表了三维中的一个面。我们射线公式P=O+Dt，在x分量上可以用；

Ox + tDx = B0x

来计算出射线击中面x=B0x时的t值：

t0x = (B0x - Ox) / Dx

盒子的6个平面都可以用该公式：

t0x = (B0x - Ox) / Dx
t1x = (B1x - Ox) / Dx
t0y = (B0y - Oy) / Dy
t1y = (B1y - Oy) / Dy
t0z = (B0z - Oz) / Dz
t1z = (B1z - Oz) / Dz

我们现在仅考虑2D的情况，如图：

由于射线和方形至多有2个交点，因此我们在计算bounds[0]的x面还是y面上只要经过简单的判断:

t0x = (B0x - Ox) / Dx 
t0y = (B0y - Oy) / Dy 
tmin = (t0x > t0y) ? t0x : t0y

即t0x和t0y哪个大则是我们的tmin值。同理tmax为：

t1x = (B1x - Ox) / Dx 
t1y = (B1y - Oy) / Dy 
tmax = (t1x < t1y) ? t1x : t1y

这时，较小才是我们的交点。这里还有两种情况则是没有交点，即：

我们可以写出：

if (t0x > t1y || t0y > t1x) 
    return false

当我们要延伸到3D的情况时，只需要把刚才获得的tmin和tmax继续和t0z和t1z做刚才相同的运算即可。有：

t0z = (B0z - Oz) / Dz 
t1z = (B1z - Oz) / Dz 
if (tmin > t1z || t0z > tmax) return false 
if (t0z > tmin) tmin = t0z 
if (t1z < tmax) tmax = t1z

因为3D中6个面的box和射线的交点也是至多只有两个。我们来看一下完整的求交代码：

bool intersect(const Ray &r) 
{ 
    float tmin = (min.x - r.orig.x) / r.dir.x; 
    float tmax = (max.x - r.orig.x) / r.dir.x; 
 
    if (tmin > tmax) swap(tmin, tmax); 
 
    float tymin = (min.y - r.orig.y) / r.dir.y; 
    float tymax = (max.y - r.orig.y) / r.dir.y; 
 
    if (tymin > tymax) swap(tymin, tymax); 
 
    if ((tmin > tymax) || (tymin > tmax)) 
        return false; 
 
    if (tymin > tmin) 
        tmin = tymin; 
 
    if (tymax < tmax) 
        tmax = tymax; 
 
    float tzmin = (min.z - r.orig.z) / r.dir.z; 
    float tzmax = (max.z - r.orig.z) / r.dir.z; 
 
    if (tzmin > tzmax) swap(tzmin, tzmax); 
 
    if ((tmin > tzmax) || (tzmin > tmax)) 
        return false; 
 
    if (tzmin > tmin) 
        tmin = tzmin; 
 
    if (tzmax < tmax) 
        tmax = tzmax; 
 
    return true; 
}

为了使代码更加快，强壮，我们用以下代码替换交换操作：

if (ray.dir.x >= 0) { 
    tmin = (min.x - r.orig.x) / ray.dir.x; 
    tmax = (max.x - r.orig.x) / ray.dir.x; 
} 
else { 
    tmin = (max.x - r.orig.x) / ray.dir.x; 
    tmax = (min.x - r.orig.x) / ray.dir.x; 
}

但是这样其实会有一个问题，IEEE中-0==0是返回true的，即当-0进入判断时仍会进入第一个分支，然后返回+∞，而不是我们要的-∞。因此我们在稍微改为：

Vec3f invdir = 1 / ray.dir; 
if (invdir.x >= 0) { 
    tmin = (min.x - r.orig.x) * invdir.x; 
    tmax = (max.x - r.orig.x) * invdir.x; 
} 
else { 
    tmin = (max.x - r.orig.x) * invdir.x; 
    tmax = (min.x - r.orig.x) * invdir.x; 
}

这样便可以避免此情况了。我们看BOX求交完整代码：

class Ray 
{ 
public: 
    Ray(const Vec3f &orig, const Vec3f &dir) : orig(orig), dir(dir) 
    { 
        invdir = 1 / dir; 
        sign[0] = (invdir.x < 0); 
        sign[1] = (invdir.y < 0); 
        sign[2] = (invdir.z < 0); 
    } 
    Vec3 orig, dir;       // ray orig and dir 
    Vec3 invdir; 
    int sign[3]; 
}; 
 
bool intersect(const Ray &r) const 
{ 
    float tmin, tmax, tymin, tymax, tzmin, tzmax; 
 
    tmin = (bounds[r.sign[0]].x - r.orig.x) * r.invdir.x; 
    tmax = (bounds[1-r.sign[0]].x - r.orig.x) * r.invdir.x; 
    tymin = (bounds[r.sign[1]].y - r.orig.y) * r.invdir.y; 
    tymax = (bounds[1-r.sign[1]].y - r.orig.y) * r.invdir.y; 
 
    if ((tmin > tymax) || (tymin > tmax)) 
        return false; 
    if (tymin > tmin) 
        tmin = tymin; 
    if (tymax < tmax) 
        tmax = tymax; 
 
    tzmin = (bounds[r.sign[2]].z - r.orig.z) * r.invdir.z; 
    tzmax = (bounds[1-r.sign[2]].z - r.orig.z) * r.invdir.z; 
 
    if ((tmin > tzmax) || (tzmin > tmax)) 
        return false; 
    if (tzmin > tmin) 
        tmin = tzmin; 
    if (tzmax < tmax) 
        tmax = tzmax; 
 
    return true; 
}

这里我们用sign数组提前保存了光线方向xyz的符号，如果是负号，则替换min和max的值，这样的提前计算可以节省15%左右的时间。

三角形

射线和三角形求交是最常见的求交方式了，现在的求交都是通过三角剖分将多边形转换成三角形，利用射线和三角形求交，来解决所有问题，而不用根据不同的形状，编写不同的求交函数。

我们仍然从和面相交开始，观察下图：

我们面公式为：

其中面的法线N(A,B,C)。我们可以获得：

float D = -1*dotProduct(N, v0);

我们用交点P=O+tR带入方程，得：

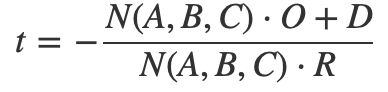
有代码：

float t = - (dot(N, orig) + D) / dot(N, dir);

若计算得t<0，则表明三角形在我们摄像机后面，我们忽略它。

当我们完成判断是否与平面相交后，我们还需要判断交点是否在三角形的内部。我们观察下图：

根据右手定则，假设我们三角形的顶点连接顺序为v0，v1，v2则我们的三角形法线指向屏幕外，当我们v0v1和v0P的叉积同样指向屏幕外，即它们的叉积和法线的点积大于零，则表明P点在v0v1的左侧，当对3条边都执行此操作后都在左边，则可以表明P点在三角形内部，即射线和三角形相交。代码：

bool rayTriangleIntersect( 
    const Vec3f &orig, const Vec3f &dir, 
    const Vec3f &v0, const Vec3f &v1, const Vec3f &v2, 
    float &t) 
{ 
    // 计算平面法线
    Vec3f v0v1 = v1 - v0; 
    Vec3f v0v2 = v2 - v0; 
    // no need to normalize
    Vec3f N = v0v1.crossProduct(v0v2);
    float area2 = N.length(); 
 
    // 判断射线是否与平面平行，平行则退出
    float NdotRayDirection = N.dotProduct(dir); 
    if (fabs(NdotRayDirection) < kEpsilon) // 几乎为0 
        return false; 
 
    // 计算D
    float d = -1.0*N.dotProduct(v0); 
 
    // 计算t
    t = -1.0*(N.dotProduct(orig) + d) / NdotRayDirection; 
    // 检查是否三角形在摄像机后面
    if (t < 0) return false; 
 
    // 计算P点位置
    Vec3f P = orig + t * dir; 
 
    // 测试是否在三角形内部
    Vec3f C; 
 
    // 第一条边
    Vec3f edge0 = v1 - v0; 
    Vec3f vp0 = P - v0; 
    C = edge0.crossProduct(vp0); 
    if (N.dotProduct(C) < 0) return false; 
 
    // 第二条边
    Vec3f edge1 = v2 - v1; 
    Vec3f vp1 = P - v1; 
    C = edge1.crossProduct(vp1); 
    if (N.dotProduct(C) < 0)  return false; 
 
    // 第三条边
    Vec3f edge2 = v0 - v2; 
    Vec3f vp2 = P - v2; 
    C = edge2.crossProduct(vp2); 
    if (N.dotProduct(C) < 0) return false;
 
    return true; // 击中三角形
}

求解重心坐标

我们在求和三角形的交点时，还有一个非常重要的是求得重心坐标，即我们需要知道P点的颜色值，纹理坐标或者法线等插值方式：

我们可以如上图所示，来获取重心坐标(w,u,v)。三角形三个点A，B，C的值可以是位置，纹理坐标等。P点的属性插值公式为：

$P_{s}=wA_{s}+uB_{s}+vC_{s}$

其中s表示属性(如位置)，w+u+v=1，我们w，u，v是相应的面积占总面积的比值：

我们计算出u，v，则也可以计算出w的值了。完整三角形插值代码如下：

bool rayTriangleIntersect( 
    const Vec3f &orig, const Vec3f &dir, 
    const Vec3f &v0, const Vec3f &v1, const Vec3f &v2, 
    float &t, float &u, float &v) 
{ 
    // 计算面法线
    Vec3f v0v1 = v1 - v0; 
    Vec3f v0v2 = v2 - v0; 
    // 不需要单位化，需要其面积
    Vec3f N = v0v1.crossProduct(v0v2); 
    float area2 = N.length(); //2倍的三角形面积
 
    // 判断是否平行
    float NdotRayDirection = N.dotProduct(dir); 
    if (fabs(NdotRayDirection) < kEpsilon) //kEpsilon很小的值
        return false; 
 
    // 计算D
    float d = -1.0*N.dotProduct(v0); 
 
    // 计算t
    t = -1.0*(N.dotProduct(orig) + d) / NdotRayDirection; 
    // check if the triangle is in behind the ray
    if (t < 0) return false; //三角形在后面
 
    // 计算P
    Vec3f P = orig + t * dir; 
    
    //判断点是否在三角形内
    Vec3f C;
 
    // 边 1
    Vec3f edge0 = v1 - v0; 
    Vec3f vp0 = P - v0; 
    C = edge0.crossProduct(vp0); 
    if (N.dotProduct(C) < 0) return false; 
 
    // 边 2
    Vec3f edge1 = v2 - v1; 
    Vec3f vp1 = P - v1; 
    C = edge1.crossProduct(vp1); 
    u = C.length() / area2; //计算u的值
    if (N.dotProduct(C) < 0)  return false; 
 
    //  边 3
    Vec3f edge2 = v0 - v2; 
    Vec3f vp2 = P - v2; 
    C = edge2.crossProduct(vp2); 
    v = C.length() / area2; //计算v的值
    if (N.dotProduct(C) < 0) return false;  
 
    return true; //击中三角形
}

一种快速的三角形求交算法

该方法来自Möller & Trumbore.的“Fast, Minimum Storage Ray/Triangle Intersection”这一篇文章中。

假设三角形ABC内有一个点P。如果我们以任何方式变换三角形（例如，如果对三角形进行平移，旋转或缩放），则在三维笛卡尔坐标系x，y，z中表示的点P的坐标将发生变化。另一方面，如果使用重心坐标表示P的位置，则应用于三角形的变换将不会影响相交点的重心坐标。如果旋转，缩放，拉伸或平移了三角形，则定义P相对于顶点A，B和C的位置的坐标u，v不会改变（请参见图1）。 MT算法正在利用此属性。实际上，作者所做的是定义一个新的坐标系，其中P的坐标不是根据x，y和z而是按照u和v来定义。我们可以很好地在不同的坐标系中定义一个点（ x，y，z空间或u，v空间）。现在，根据我们的了解，u和v坐标不能大于1或小于0。它们的总和也不能大于1（u + v <= 1）。实际上，它们表示在单位三角形内定义的点的坐标（这是在u，v空间中由顶点（0，0），（1、0），（0，1）定义的三角形，如下图所示）：

我们已经根据从一个参数空间到另一个参数空间（从xyz空间到uv空间）的u和v重心坐标重新解释了点P的三维x，y，z位置。我们还了解到，在uv空间中定义的点在单位三角形内。

具有三个未知数：u，v和t。从几何上讲，我们已经解释了u和v的含义。但是t呢？简单：我们将认为t是我们刚刚介绍的u和v坐标系的第三轴。现在，我们有了由三个轴u，v和t定义的坐标系。但是，再次从几何上讲，这意味着什么。实际上，我们知道t表示从射线原点到交点P的距离。如上图，我们可以看到已经创建了一个坐标系统，该系统使我们能够以重心坐标和从射线原点到三角形上该点的距离来完全表示交点P的位置。我们看公式：

根据：

带入上述方程：

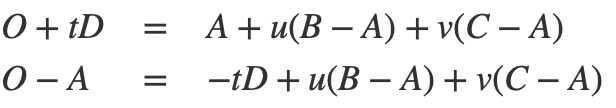
我们用矩阵形式表示：

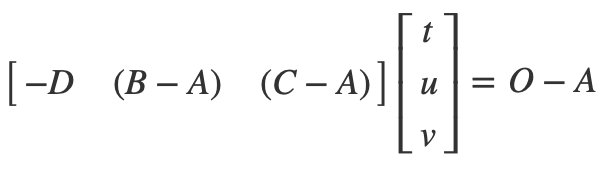
我们这里使用克莱姆法则(Cramer's Rule)对其求解。克莱姆法则表示，若有矩阵运算：

$M*\begin{bmatrix} x\\ y \\ z \end{bmatrix}=C$

我们想求[x,y,z]的值可以通过构造Mx，My，Mz矩阵，构造方法为用C替换M中相应的列，如Mx为用c替换M中的x列(即第一列)。最后：

$x=\frac{\left | M_{x} \right |}{\left | M \right |}$

$y=\frac{\left | M_{y} \right |}{\left | M \right |}$

$z=\frac{\left | M_{z} \right |}{\left | M \right |}$

|x|表示矩阵x的行列式。因此我们三角形求交的公示中M为[-D, B - A, C - A]，X为[t, u, v]，C为(O-A) 。为了方便观察我们令T=O−A，E1=B−A，E2=C−A。根据克莱姆法则可得：

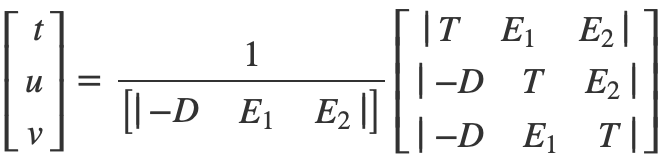
化简行列式得：

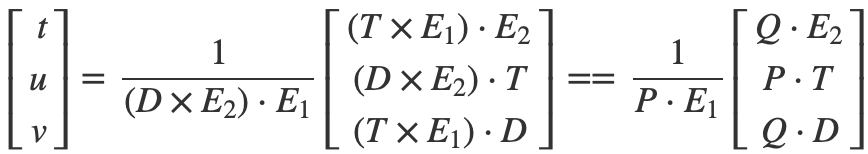
其中令P=(D×E2)，Q=(T×E1)。接下来我们的三角形求交代码可以有更快速轻便的形式：

bool rayTriangleIntersect(
    const Vec3f &v0, const Vec3f &v1, const Vec3f &v2,
    const Vec3f &orig, const Vec3f &dir,
    float &tnear, float &u, float &v)
{
    Vec3f edge1 = v1 - v0;
    Vec3f edge2 = v2 - v0;
    Vec3f pvec = crossProduct(dir, edge2);//P=D叉乘E2
    float det = dotProduct(edge1, pvec);//P点乘E1
    if (det == 0 || det < 0) return false;//不存在的情况(平行或背面)

    Vec3f tvec = orig - v0;
    u = dotProduct(tvec, pvec);
    if (u < 0 || u > det) return false;//u最后的值只能在[0,1]

    Vec3f qvec = crossProduct(tvec, edge1);//Q=T叉乘E1
    v = dotProduct(dir, qvec);
    if (v < 0 || u + v > det) return false;//u+v最后的值只能在[0,1]

    float invDet = 1 / det;

    tnear = dotProduct(edge2, qvec) * invDet;
    u *= invDet;
    v *= invDet;


    return true;
}

0小龙虾0

关注

18
点赞
踩
59

收藏

觉得还不错? 一键收藏
1
评论
光线跟踪的几种常见求交运算

光线跟踪的几种常见求交运算我们知道光线跟踪中最昂贵的就是和几何对象的求交运算了。这里就记录几个比较常见的光线和几何对象求交运算。球射线与球体相交可能是射线几何相交测试的最简单形式，这就是为什么这么多射线追踪器显示球体图像的原因。由于其简单性，它还具有非常快的优势。可以使用两种方法实施此测试。第一个使用几何来解决问题。第二种技术是我们最常用的方法，我们称它为代数法。这都...
复制链接

扫一扫