函数项级数与幂级数

基本概念

定义

幂级数是包含在函数项级数里的，函数项级数又带$n$又带$x$，当函数项级数的$x$是定值（常数）时，就变成了常数项级数

和函数：

$$S(x)=\sum _{n=1}^{\infty }{u}_n(x)$$且和函数的定义域对应原级数的收敛域

幂级数：

形如${\sum }_{n=1}^{\infty }{a}_n(x-x_0{)}^n$称为在$x_0$处的幂级数

收敛域的求法

收敛区间是开区间，收敛域可能有闭区域，即收敛区间+端点性质=收敛域

幂级数的性质

1. 幂级数的和函数在其收敛域$I$上连续
2. 和函数逐项积分后所得到的幂级数和原幂级数有相同的收敛半径
3. 逐项求导后所得到的幂级数和原幂级数有相同的收敛半径

幂级数的运算

泰勒级数

求级数的和函数要先求收敛域

泰勒级数是一种幂级数只展到n阶叫泰勒展开式，能无限展下去叫泰勒级数

$$\begin{gathered} \frac{1}{1-x}=\sum _{x=0}^{\infty }{x}^n=1+x+x^2+...+x^n+...\text{ , }x\in (-1,1) \\ \frac{1}{1+x}=\sum _{x=0}^{\infty }(-1{)}^n{x}^n=1-x+x^2+...+(-1{)}^n{x}^n+...\text{ , }x\in (-1,1) \end{gathered}$$

记忆技巧：

$$\frac{1}{1+x}=\frac{1}{1-(-x)}=\sum _{x=0}^{\infty }(-x{)}^n$$

---

$e^x$、$\sin x$和$\cos x$的x取值范围均是$x\in (-\infty ,\infty )$
而$\ln (1+x)$则是$x\in (-1,1]$
而$(1+x{)}^a$、$\frac{1}{1-x}$、$\frac{1}{1+x}$则是$x\in (-1,1)$

---

$\sin x$和$\cos x$求导会出现负项，所以是正负交替的，另外$\sin x^{\prime }=\cos x$所以$\sin x$级数求导就是$\cos x$的级数，即下式

$$\sum _{x=0}^{\infty }(\frac{(-1{)}^n}{(2n+1)!}\cdot x^{2n+1}{)}^{\prime }=\sum _{x=0}^{\infty }(\frac{(-1{)}^n}{2n!}\cdot x^{2n})$$

---

$$\sum _{x=0}^{\infty }\frac{x^{2n}}{(2n)!}=\sum _{x=0}^{\infty }\frac{x^n}{n!}+\sum _{x=0}^{\infty }\frac{-x^n}{n!}$$

因为$n$为奇数会抵消

幂级数收敛半径的求法

x^n的重要推论

等比级数

$$\sum _{n=0}^{\infty }{x}_n=\frac{1}{1-x},|x|<1$$

上面提到了两个重要的性质如下

• 和函数逐项积分后所得到的幂级数和原幂级数有相同的收敛半径
• 逐项求导后所得到的幂级数和原幂级数有相同的收敛半径

如果对这个式子求导，并且两侧同乘一定数量的$x$使左侧为$x^n$会得到下式

$$\sum _{n=0}^{\infty }n{x}^n=(\frac{1}{1-x}{)}^{\prime }x,|x|<1$$
如法炮制则如下
$$\sum _{n=0}^{\infty }n(n-1)x^n=(\frac{1}{1-x}{)}^{\prime \prime }{x}^2,|x|<1$$

---

那么对于一个级数${\sum }_{n=0}^{\infty }(a{n}^2+bn+c)x^n$就可以用上面的仨表示

$$a{n}^2+bn+c=\{\begin{array}{r}c\cdot 1\\ (a+b)\cdot n\\ a\cdot n(n-1)\end{array}$$
所以可以分解成这样的组合：

$$\sum _{n=0}^{\infty }(a{n}^2+bn+c)x^n=\{\begin{array}{l}c\cdot 1{\sum }_{n=0}^{\infty }1\cdot x^n\\ (a+b)\cdot x{\sum }_{n=0}^{\infty }n{x}^{n-1}\\ a\cdot x^2{\sum }_{n=0}^{\infty }n{x}^{n-2}\end{array}$$

在接下来就写成了
$$c\frac{1}{1-x}+(a+b)x(\frac{1}{1-x}{)}^{\prime }+a{x}^2(\frac{1}{1-x}{)}^{\prime \prime }$$

题目与思路

基本性质类

等比级数部分和公式

$$S(x)=\frac{a_0}{1-q}\text{ ,}其中q是公比$$

例如$$\sum _{n=0}^{\infty }{x}^{2n+1}=\frac{x}{1-x^2}$$

（以下内容与本小节标题无关）

$$\sum _{n=0}^{\infty }(2n+1)x^{2n}=(\sum _{n=0}^{\infty }{x}^{2n+1}{)}^{\prime }={\frac{x}{1-x^2}}^{\prime }$$

显然这种方法比下面简单：

$$\sum _{n=0}^{\infty }(2n+1)t^n\text{ ,}随后带入t=x^2$$

上式的具体处理做法是拆成两个式子

$$\sum _{n=0}^{\infty }(2n+1)t^n=\sum _{n=0}^{\infty }{t}^n+2t\sum _{n=0}^{\infty }n{t}^{n-1}$$

展开类

将函数展开成幂级数

知乎 - 数学技巧篇43：函数展开成幂级数方法

就是找出一个$$f(x)=\sum _{n=0}^{\infty }{a}_n(x-x_0{)}^n=\sum _{n=0}^{\infty }\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n$$

（图源网络）

某些特殊的形式可由上面的变换而来，例如$\frac{1}{n!}$其实就是$e^x$在$x=1$时的展开式，逆向操作就是对要展开的式子补$x$，然后展开后给$x$取特殊值。

比如$e^x$展成$x-3$的级数，即改成$e^3\cdot e^{x-3}$，然后展后面的即可

某点高阶导数取值

利用泰勒展开后的形式，某阶导数会出现在展开式中
$$f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n$$

若求$f^{(5)}(0)$，即根据泰勒展开式的定义，可以确定$x_0=0$。然后找展开式子中含$x^5$的地方的系数

$$x^2\cdot e^{\frac{x}{3}}=x^2[1+(\frac{x}{3})+\frac{1}{2!}(\frac{x}{3}{)}^2+\frac{1}{2!}(\frac{x}{3}{)}^2+...]$$

即$$\frac{f^{(5)}(0)}{5!}{x}^5=x^2\cdot \frac{1}{3!}(\frac{x}{3}{)}^3\to \frac{f^{(5)}(0)}{5!}=\frac{1}{3!\cdot 9}$$

$\ln (f(x))$的幂级数展开

$$\ln (2+x)=\ln (1+1+x)=(1+x)-\frac{(1+x{)}^2}{2}+\frac{(1+x{)}^3}{3}...$$

这是$1+x$的幂级数，不是$x$的幂级数

$$\ln (2+x)=\ln 2(1+\frac{x}{2})=\ln 2+\ln (1+\frac{x}{2})$$

展$\ln (1+\frac{x}{2})$才对

特殊展开式的预处理

$${\sin }^{2}x=\frac{1-\cos 2x}{2}$$

收敛相关类

某处条件收敛的意义

利用广义性，换$x-1=t$，即可以转换为${\sum }_{x=0}^{\infty }{a}_n{t}^n$在$t=1$处条件收敛，然而条件不确定点只能是边界，小于这个点一定收敛，大于这个点一定发散，所以收敛半径是1
又由于$-1<t=x-1<1$则$0<x<2$，选D

求收敛区间

• 先计算收敛半径再看端点
• 或者直接求收敛区间

这里根值审敛开$2n-1$或者$n$都行，右边的式子同理。左侧的式子是这样，其中$\frac{1}{|x|}$是常数，开$n$次方为1

$$\sqrt[n]{\frac{2^{2n}\cdot \frac{1}{2}}{2n-1}\cdot |x{|}^{2n}\cdot \frac{1}{|x|}}=4\cdot x^2<1$$

右式如法炮制，然后收敛半径取两者之间较小的

其他技法

$$\begin{gathered} S(x)=\sum _{n=1}^{\infty }\frac{x^n}{n}=-\ln (1-x)\text{ ,}-1\le x<1 \\ S(x)=\sum _{n=1}^{\infty }n{x}^{n-1}=\frac{1}{(1-x{)}^2},\text{ ,}-1<x<1 \end{gathered}$$

广义性的使用

指的是比如说对于和函数

$$\sum _{n=2}^{\infty }\frac{x^n}{n-1}\to \sum _{n=1}^{\infty }\frac{x^{n+1}}{n}$$

另一方面$$\sum _{n=1}^{\infty }\frac{x^n}{n}=-\ln (1-x)$$

则有${\sum }_{n=1}^{\infty }\frac{x^{n+1}}{n}=-x\ln (1-x)$

如果提出去的不是$x$而是$\frac{1}{x}$，则$x$的定义域还应注明$x\ne 0$，当然，$x$原本的定义域尤其是两端到底能不能取到需要按题意进行处理

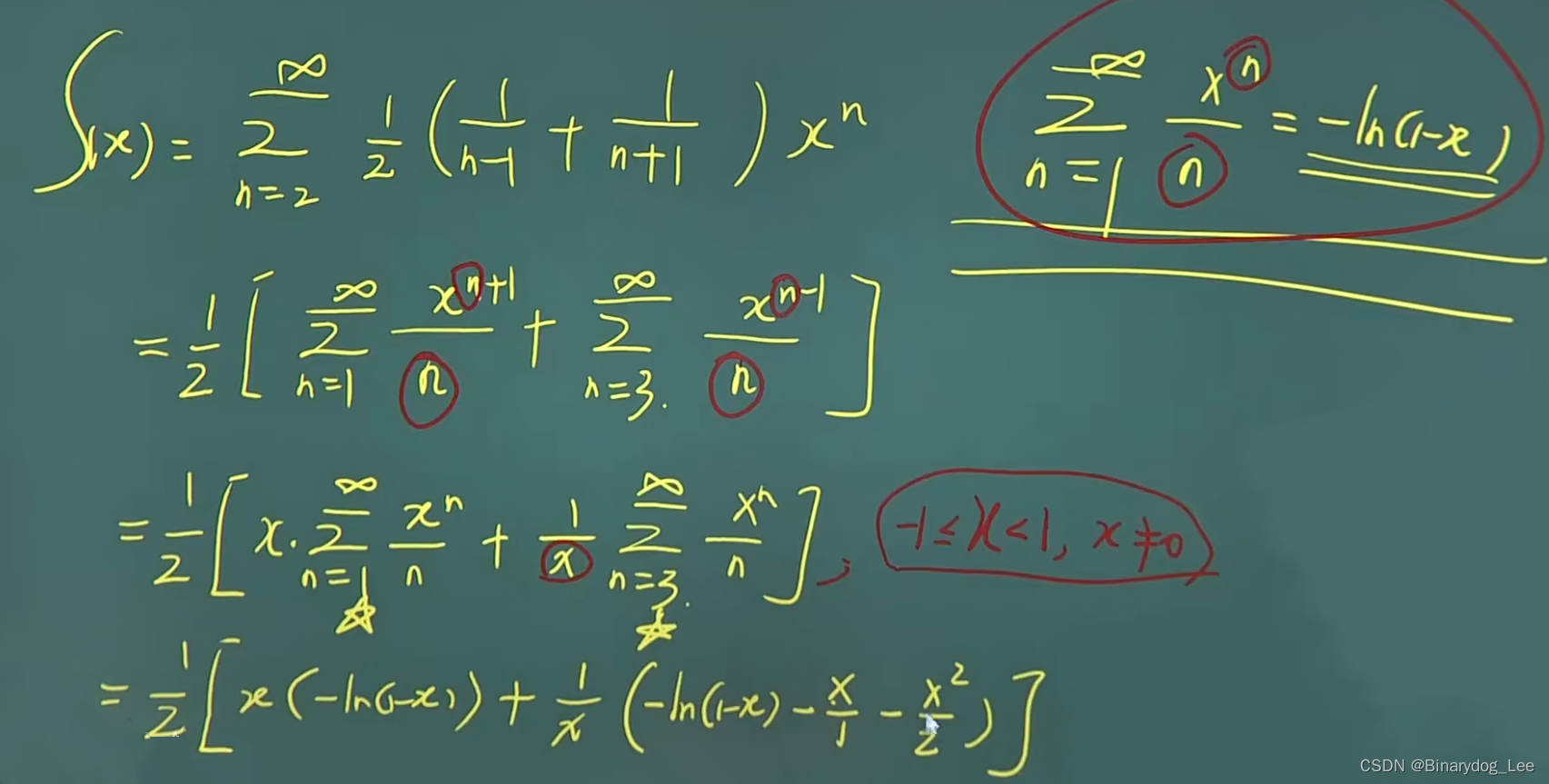
（上图补充：还少了$S(0)$时的情况，因为写定义域时排除了$x=0$，对于这种情况还得单独求出来）

常数项级数构造幂级数

1993数学一

关于收敛半径是1的解释：对$n^2-n+1$使用根值判别法，为什么不把$x^2$考虑在内？因为是要求$x$的范围的，先当成范围边界的常数看（最后使用的时候也是$x=\frac{1}{2}$具体常数）

然后$\frac{1}{R}={\lim }_{n\to \infty }\sqrt[n]{n^2-n+1}$求出$R=1$，处理方法是幂指函数，接着便有

$$S(x)=\sum _{n=0}^{\infty }(n^2-n+1)x^n-1$$

为啥减一？因为下标$n$变为了从0开始才能使用下面的变换，但是0又不在题目范围内，还得减去$n=0$的具体值

紧接着是下面的内容，即利用性质（参见另一篇博客：函数项级数与幂级数的内容）配出$(n^2-n+1)x^n$

$$\sum _{n=0}^{\infty }{x}^n=\frac{1}{1-x},|x|<1$$