概率论与数理统计

部分内容总结自张宇和考研竞赛凯哥

概率论基础

• $AB$互不相容时，不仅$P(ABC)=0$，而且$P(ABC)=0$
• 一事件发生概率为1，不能断定该事件为全集。
• $P(A)>0,P(B)>0$时互斥和独立不能同时成立
• 互斥则$P(A\cup B)=P(A)+P(B)$
• 互斥则$A\subseteq \overline{C}$，此时$P(A\overline{C})=P(A)$

条件概率

见到条件概率如果没有独立性就直接写出公式

$$P(A|B)=1-P(\overline{A}|B)$$

常见分布

• 几何分布的取点是离散的整数点
• 泊松分布是单位时间内独立事件发生次数的概率分布，指数分布是独立事件的时间间隔的概率分布。

二项分布概率最大项K

已知X~B(n,p)，则要使 P(x=k0）最大

• 当$(n+1)p$为整数时，$k0=(n+1)p$,或 $k0=(n+1)p-1$
• 当$(n+1)p$不是整数时，$k0=(n+1)p向下取整$

其实就是前后项作比化简出来的

分布函数

三大性质

• 单调不减
• $F(-\infty )=0,F(\infty )=1$
• 右连续

$F(x)$是分布函数，那$F(2x-1)$是分布函数，但$1-F(-x)$不是，因为它是左连续的

---

【例】假设随机变量$X$的绝对值不大于1， P { X = − 1 } = 1 8 P\{X=-1\}=\frac 18 P{X=−1}=81​， P { X = 1 } = 1 4 P\{X=1\}=\frac14 P{X=1}=41​。在事件
{ − 1 < X < 1 } \{-1<X<1\} {−1<X<1}出现的条件下，$X$在$(-1，1)$内的任一子区间上取值的条件概率与该子区间长度
成正比。试求X的分布函数 F ( x ) = P { X ≤ x } F(x)=P\{X≤x\} F(x)=P{X≤x}

【解析】

F ( x ) = { P { X < 0 } = 0 x < 1 P { X < x } − 1 ≤ x < 1 1 x ≥ 1 F(x)=\left\{ \begin{matrix} P\{X<0\}=0 &x<1 \\P\{X<x\} & -1\le x <1 \\1 & x \ge 1 \end{matrix} \right. F(x)=⎩ ⎨ ⎧​P{X<0}=0P{X<x}1​x<1−1≤x<1x≥1​

其中 P { X < x } = P { X < − 1 } + P { X = − 1 } + P { − 1 ≤ X ≤ x } = 0 + 1 8 + P { − 1 ≤ X ≤ x } P\{X<x\}=P\{X<-1\}+P\{X=-1\}+P\{-1\le X\le x\}=0+\frac 18+P\{-1\le X\le x\} P{X<x}=P{X<−1}+P{X=−1}+P{−1≤X≤x}=0+81​+P{−1≤X≤x}

而关于 P { − 1 ≤ X ≤ x } P\{-1\le X\le x\} P{−1≤X≤x}实为条件概率 P { − 1 ≤ X ≤ 1 } ⋅ P { − 1 ≤ X ≤ x ∣ − 1 ≤ X ≤ 1 } = 5 8 ⋅ x + 1 2 P\{-1\le X\le 1\}·P\{-1\le X\le x |-1\le X\le 1\}=\frac 58 ·\frac{x+1}{2} P{−1≤X≤1}⋅P{−1≤X≤x∣−1≤X≤1}=85​⋅2x+1​

概率密度

见到概率密度自然知道是连续型（是$F(x)$连续），就如同见到分布律就知道是离散型一样

1. $f(x)>0$
2. ${\int }_{-\infty }^{\infty }f(x)dx=1$

因此存在即使满足第二点${\int }_{-\infty }^{\infty }f(x)dx=1$也不是概率密度函数的情况。例如对于概率密度函数$f(x)$，则$2xf(x^2)$不是概率密度函数，即便它${\int }_{-\infty }^{\infty }2xf(x^2)dx={\int }_{-\infty }^{\infty }f(x^2)d{x}^2=1$，但是在$x<0$时它值是负的

• 概率密度函数从负无穷到正无穷还有e的平方幂，直接鉴定为正态分布

具有相同概率密度

$X$和$-X$有相同的概率密度
⇔ F ( x ) = P { − X ≤ x } \Leftrightarrow F(x)=P\{-X\le x\} ⇔F(x)=P{−X≤x}

期望的计算

两个独立随机变量，乘积的期望等于期望的乘积，即$E(XY)=EX\cdot EY$

上面这句话的一种经典情况是，$E(X^2)\ne EX\cdot EX$

证明独立

相关一定不独立，不相关只是没有线性关系，不代表不相关。得构造事件并验证$p(AB)=p(A)\cdot p(B)$是否成立，若成立则独立

独立性的另一个标志是：$P(B|A)=P(B|\overline{A})$，即不管$A$是否发生，$B$发生的概率都一样，即二者无关，即独立

独立的充要条件是$P(A|B)=P(A)$，即条件对结果不影响，一种可能会出现的复杂形式如下（用作例子）

$$\begin{gathered} P(A\cup B|C)=P(A\cup B) \\ \Rightarrow P(A|C)+P(B|C)-P(AB|C)=P(A)=P(B)-P(AB) \end{gathered}$$

---

一般情况下不独立，举反例即可

函数的分布

积分为$\pi$

$${\int }_{-\infty }^{\infty }{e}^{-t^2}dt=\sqrt{\pi }$$不仅可以用标准化为正态来做，也可以用上面这个化简

---

那么像$$f(x)=A{e}^{-x^2+x}$$

泊松分布与泰勒展开

λ是事件的平均发生率（单位区间内事件发生的平均发生次数）。

注意泊松分布的$k$得从0开始，不从$0$开始的就不是
P { x = k } = λ k k ! e − λ , k = 0 , 1 , 2 , . . . P\{x=k\}=\frac{\lambda^k}{k!}e^{-\lambda},k=0,1,2,... P{x=k}=k!λk​e−λ,k=0,1,2,...

对它每项相加则可得

$$e^{-\lambda }\sum _{k=0}^{\infty }\frac{{\lambda }^k}{k!}=e^{-\lambda }{e}^{\lambda }=1$$
而$e^x$的泰勒展开则是
$$\sum _{k=0}^{\infty }\frac{x^k}{k!}=e^x$$

概率论：多维

二维的独立性

只有矩形区域才有可能独立

验证$$f_Y(y)\cdot f{(}_X(x)=f(x,y)$$

离散型$(X,Y)$的分布律的计算

涉及到联合，都得先看两变量是否独立，不要默认独立。

联合分布律包含$p_{ij}$，也包含$X$和$Y$的边缘分布，要在整个表格上都体现出来。

并且这俩中的某些可能缺失，需要依靠剩下的补全。或者由其他信息推出这俩的部分信息，然后补全表格。其他信息是指，比如$X$和$Y$的协方差之类的东西，通过计算和变形得到能填入联合分布律表格中的一部分，随后利用表格性质补全即可。

不管$X$和$Y$是否独立，各自如果单独给出分布律是直接可以填在表格边上的边缘分布栏目中的。

二维条件分布的处理

• $f_Y(y)$是$x$任意的$Y$的分布
• $f_{Y|X}(y|x)$是$x$固定的$y$的分布（这里就把$x$当常数）

例如 P { − 1 < X < 1 ∣ Y = 2 } P\{-1<X<1|Y=2\} P{−1<X<1∣Y=2}这样的是一维，但是 P { − 1 < X < 1 ∣ Y ≤ 2 } P\{-1<X<1|Y\le2\} P{−1<X<1∣Y≤2}就是二维，按照下式计算

P { − 1 < X < 1 ∣ Y ≤ 2 } = P { − 1 < X < 1 , Y ≤ 2 } P { Y ≤ 2 } = ∬ D f ( x , y ) d σ ∫ f Y ( y ) P\{-1<X<1|Y\le2\}=\frac{P\{-1<X<1,Y\le2\}}{P\{Y\le2\}}=\frac{\iint_D f(x,y)d\sigma}{\int f_Y(y)} P{−1<X<1∣Y≤2}=P{Y≤2}P{−1<X<1,Y≤2}​=∫fY​(y)∬D​f(x,y)dσ​

关于 P { − 1 < X < 1 , Y ≤ 2 } P\{-1<X<1,Y\le2\} P{−1<X<1,Y≤2}的处理，若$x,y$独立，则化为 P { − 1 < X < 1 } ⋅ P { Y ≤ 2 } P\{-1<X<1\}·P\{Y\le2\} P{−1<X<1}⋅P{Y≤2}，若不独立则寻找积分区域按二重积分处理
关于 P { X < Y } P\{X<Y\} P{X<Y}的处理，这种只能按区域二重积分

联合边缘条件直接的关系

$$\frac{f(x,y)}{f_X(x)}=f_{Y|X}(y|x)$$

• 由$f(x,y)$求边缘就是积分
• 只知道边缘分布得不到联合分布，必须还有条件概率才行
• 求 P { X + Y > 1 } P\{X+Y>1\} P{X+Y>1}这种还是积分（主要是定区域）

ξ = min ⁡ { X , Y } \xi = \min\{X,Y\} ξ=min{X,Y}这类题目的处理

若是离散的，画表格就行，所有离散型问题的第一步都是画表格

正态分布的相加与标准化

$D(X\pm Y)=DX+DY\pm Cov(X,Y)$，在$X$和$Y$独立的情况下，$Cov(X,Y)=0$。

因此在$X\sim N({\mu }_1,{\sigma }_1^2)$和$Y\sim N({\mu }_2,{\sigma }_2^2)$独立的情况下$X+Y\sim ({\mu }_1+{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)$

---

定义：$X\sim N(\mu ,{\sigma }^2)$，则$Z=\frac{X-\mu }{\sigma }\sim N(0,1)$

一切非标准化的正态分布要标准化再做题，如 P { X ≤ μ − σ 2 } P\{X\le \mu-\sigma^2\} P{X≤μ−σ2}就化为 P { X − μ σ ≤ σ } = Φ ( σ ) P\{\frac{X-\mu}{\sigma}\le \sigma\}=\Phi(\sigma) P{σX−μ​≤σ}=Φ(σ)

均匀分布

直接椭圆面积/圆面积就出来了，不用积分

二维正态分布（降维思想）

设随机变量$X$和$Y$都服从正态分布，且它们不相关，则$X$和$Y$未必独立。

• 不知道$(X,Y)$是否服从二维正态分布
• 不知道$X+Y$是否服从一维正态分布
• 只有二维正态$\rho =0$才独立
• 已知边缘分布无法获取联合分布（对应一二条）
• 但若随机变量$X$和$Y$都服从正态分布且相互独立，则$(x,y)$服从二维正态分布
• （接上条）若$(x,y)$服从二维正态分布，则$X+Y$服从正态分布
• 服从二维正态分布的不一定$X$和$Y$相互独立

即二维到一维无条件，一维需要有条件（独立）才能升级成二维。利用降维做题

降维例题：
设$(X,Y)\sim N(\mu ,\mu ,{\sigma }^2,{\sigma }^2,0)$，则 P { X < Y 0 } = P\{X<Y0\}= P{X<Y0}=___

P { X − Y < 0 } = P { Y − X > 0 } P\{X-Y<0\}=P\{Y-X>0\} P{X−Y<0}=P{Y−X>0}，相互独立则$X\sim N(\mu ,{\sigma }^2),Y\sim N(\mu ,{\sigma }^2)$，则$Y-X\sim N(\mu ,2{\sigma }^2)$（其他题如有必要可以标准化一下）

故为1/2

数字特征

$$\begin{gathered} EX={\iint }_{D}x\cdot f(x,y)d\sigma \\ E{X}^2={\iint }_D{x}^{2}f(x,y)d\sigma \end{gathered}$$
这是积分问题

$$DX=E(X^2)-(EX{)}^2$$

函数的分布率的计算

所有分布律都得列出范围 P { X = x k } = p k , k = 1 , 2 , ⋯ P\{X=x_k\}=p_k,k=1,2,\cdots P{X=xk​}=pk​,k=1,2,⋯

本质是反解，例如下
$X\sim B(n,p)$，则$Y=n-X$服从的分布律为

P { Y = k } = P { n − x = k } = P { x = n − k } = C n n − k P n − k ( 1 − p ) n − ( n − k ) , k = 1 , 2 , ⋯ n P\{Y=k\}=P\{n-x=k\}=P\{x=n-k\}=C_{n}^{n-k}P^{n-k}(1-p)^{n-(n-k)},k=1,2,\cdots n P{Y=k}=P{n−x=k}=P{x=n−k}=Cnn−k​Pn−k(1−p)n−(n−k),k=1,2,⋯n

非独立的不要$$

$Y=f(X)$的计算

函数的分布函数的计算，就是发现$Y=f(X)$后的处理方法，本质是把$y$的范围转化为$x$的范围

通过移动横线来判断$x$的范围，按图像分段，两个点分三段，这个段是分情况下的移动横线的范围。

谁的函数给谁分段，这里是求$F_Y(y)$，那就给$y$分段，注意右连续性，即左闭右开

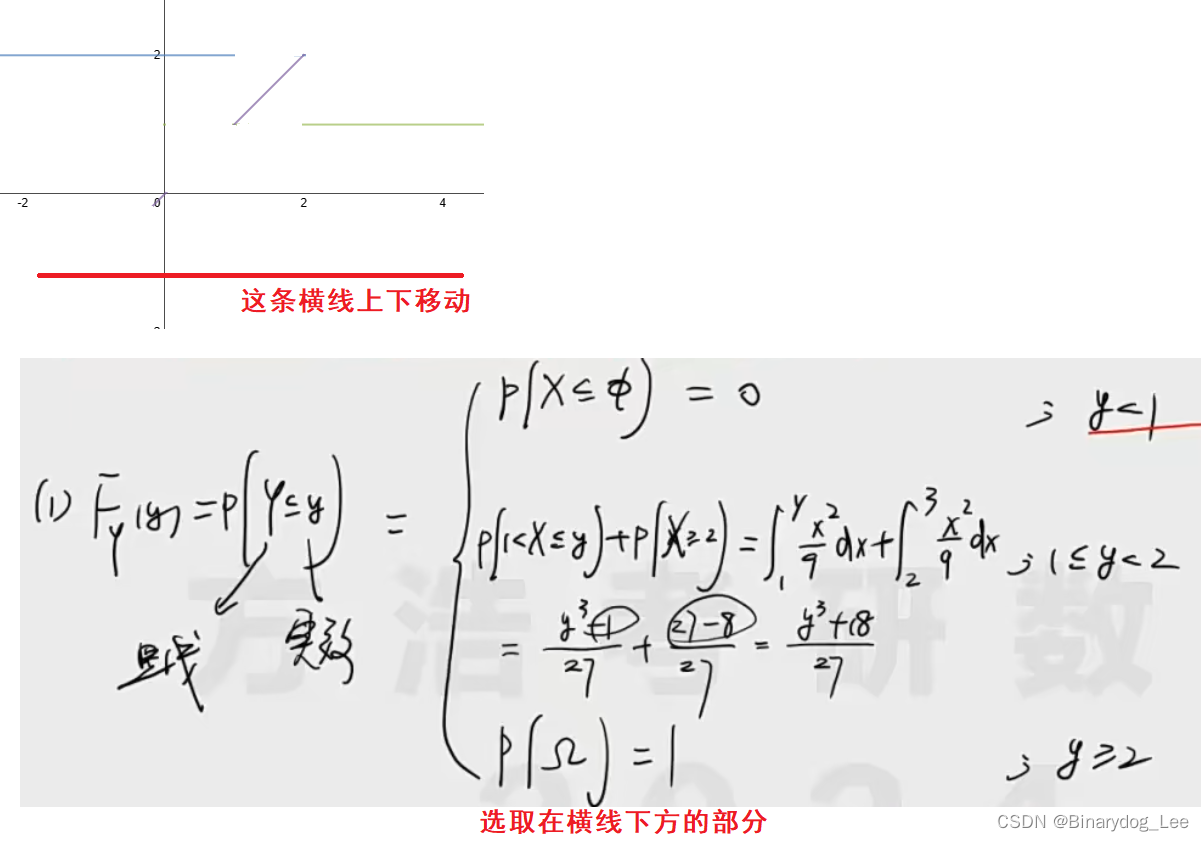
然后 P { X ≤ Y } P\{X\le Y\} P{X≤Y}即计算 P { Y − X ≥ 0 } P\{Y-X\ge0\} P{Y−X≥0}因此要看下式

P { Y − X } = { 2 − X X ≤ 1 0 1 < X < 2 1 − X X ≥ 2 P\{Y-X\} = \left\{\begin{aligned} 2-X & &X \le 1 \\ 0 & & 1<X<2\\ 1-X & & X \ge 2 \end{aligned} \right. P{Y−X}=⎩ ⎨ ⎧​2−X01−X​​X≤11<X<2X≥2​

前俩都是大于等于0的，符合题意 P { Y − X ≥ 0 } = P { X < 2 } P\{Y-X\ge0\}=P\{X<2\} P{Y−X≥0}=P{X<2}，积一下$x$的概率密度就可以了

$Z=f(X,Y)$的计算

卷积公式

$$f_Z(z)={\int }_{-\infty }^{\infty }f(x,y(x,z))|\frac{\partial y(x,z)}{\partial z}|dx$$

而范围的求法则如下：

比如说$0<x<1,0<y<1,Z=X-Y$，那就是下面的范围求交集

$$\{\begin{array}{rlr}0<x<1& \Rightarrow & 0<x<1\\ 0<x-z<1& \Rightarrow & z-1<x<z\end{array}$$

分别令$z-1$、$z$等于$0$和$1$，得到三个分段点0、1、2（有一个重复的1），然后就开始求交集

• $z<0$：没交集
• $0<z<1$：和$0<x<1$有交集$[0,z]$，这就是积分上下限，概率密度是${\int }_0^z(2-z)dx$
• $1<z<2$：和$0<x<1$有交集$[z-1,1]$，概率密度是${\int }_{z-1}^1(2-z)dx$
• $2<z$：没交集（没交集统一写“其他”）

要是求分布函数就得分四段（三个分界点）

概率论：大数定律

依概率收敛

依概率收敛的步骤说白了就两点

1. 构造$|X_n-a|<\epsilon$
2. 求极限 lim ⁡ n → ∞ P { ∣ X n − a ∣ < ε } \lim _{n \to \infty}P\{|X_n-a|<\varepsilon\} limn→∞​P{∣Xn​−a∣<ε}（此处多用夹逼准则）

然后就证出来$X_n\stackrel{P}{\to }a$

数理统计：基础

含$X_i$的期望

最基本的方法就是把$E(f(x))$拆成多个期望相加的式子

乘积的期望不一定等于期望的乘积，除非两者独立。如果两者不独立（比如$X_i$和$\overline{X}$）就得用别的方法，例如把下式：

$$E(X_i\overline{X})=E{X}_i\cdot \frac{X_1+X_2+\dots +X_n}{n}=\frac{1}{n}[E{X}_1^2+E{X}_1{X}_2+\dots +E{X}_1{X}_n]$$

其中$E{X}_1^2$的两个参数不独立，使用$DX=E(X^2)-(EX{)}^2$，其他的均独立，乘积的期望等于期望的乘积，即都等于$(EX{)}^2$

含$X_i$的协方差

使用协方差运算法则
$$\begin{gathered} Cov(X,X)=DX \\ Cov(X,Y)=Cov(Y,X) \\ Cov(aX,bY)=abCov(X,Y) \\ Cov(X+a,Y+b)=Cov(X,Y) \\ Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_2,Y) \end{gathered}$$

另一方面由于协方差描述的是两个变量总体误差的期望，即$Cov(X,Y)=E[(X-EX)(Y-EY)]=EXY-EXEY$，所以通常有
$$Cov(X_1,\overline{X})=Cov(X_2,\overline{X})$$

当然这里的运算依然是参考前面的内容，先展开$\overline{X}$，之后再利用运算法则提出$\frac{1}{n}$，随即利用分配律处理。并且由于$X_i$和$X_n$是独立同分布的，所以$Cov(X_1,X_n)=0$

含$X_i$的方差

主要以使用公式$D(X\pm Y)=DX+DY\pm 2Cov(X,Y)$为主，若协方差不好求，则按上面的方法，将$\overline{X}$展开处理。展开的多项式使用$D(aX)=a^{2}DX$等方法处理

$E(S^2)=DX={\sigma }^2$的证明

$S^2$是样本方差

$E(S^2)$的处理

主要依靠公式：$E(S^2)=DX={\sigma }^2=E(X^2)-(EX{)}^2$，另一方面

$$E(X^2)={\int }_{-\infty }^{+\infty }{x}^{2}f(x)dx$$

积分时记得利用积分性质（对称性啥的）

---

另一种方法参见下方的“来自一个正态总体的抽样分布”章节的结论2，可以采用它的变式

含$D\overline{X}$的处理

$D\overline{X}=\frac{1}{n}DX$确实成立，但是前提是$n$项平均值。如果是$2n$项就不成立

2001年题

$$\overline{X}=\frac{1}{2n}\sum _{i=0}^{2n}{X}_i$$

那$D\overline{X}=\frac{1}{2n}DX$

其他

$$Z=\sum _{i=1}^n(X_i-\overline{X}{)}^2\Rightarrow EZ=(n-1)E(S^2)=(n-1)DX$$

数理统计：三大分布

再三大分布的语境下，遇到不是标准正态分布的首先应当先标准化，即 $$\frac{x-\mu }{\sigma }\sim N(0,1)$$

正态+正态不一定还是正态

• 若$X$和$Y$都是正态分布，则$X+Y$不一定是正态分布
• 若$X$和$Y$都是正态分布，则$(X+Y)$不一定是二维正态分布
• 若$(X,Y)$是二维正态分布，则$X$和$Y$都是正态分布
• 若$X$和$Y$都是正态分布，且$X$和$Y$独立，则$X+Y$是正态分布，$(X,Y)$是二维正态分布，且$\rho =0$
• 若$X$是正态分布，那么$aX+b(a\ne 0)$也是正态分布
• 若对于$\forall aX+bY$均为正态分布，则$(X,Y)$服从二维正态分布
• 若$(X,Y)$是二维正态分布，且
  $$如果UV满足\{\begin{array}{r}U=a_{1}X+b_{1}Y\\ V=a_{2}X+b_{2}Y\end{array}\Rightarrow 则当\begin{array}{c}\left|\begin{array}{cc}{a}_1& b_1\\ a_2& b_2\end{array}\right|\end{array}\ne 0时，(U,V)服从二次正态分布$$

那个矩阵啥意思？意思就是不是同比例的

符合某某分布，多半问题出在样本需要符合$N(0,1)$，然后问题由此展开。常用到正态分布的相加（见概率论部分的正态分布的相加小节）。并且通过某些变换（除以某些数之类的），常可以把$X_1\pm X_2$这种视为一个新的$X_n\sim N(0,1)$

来自一个正态总体的抽样分布

3的本质就是卡方分布的定义

区间估计

分为$\sigma$已知和未知两种情况。

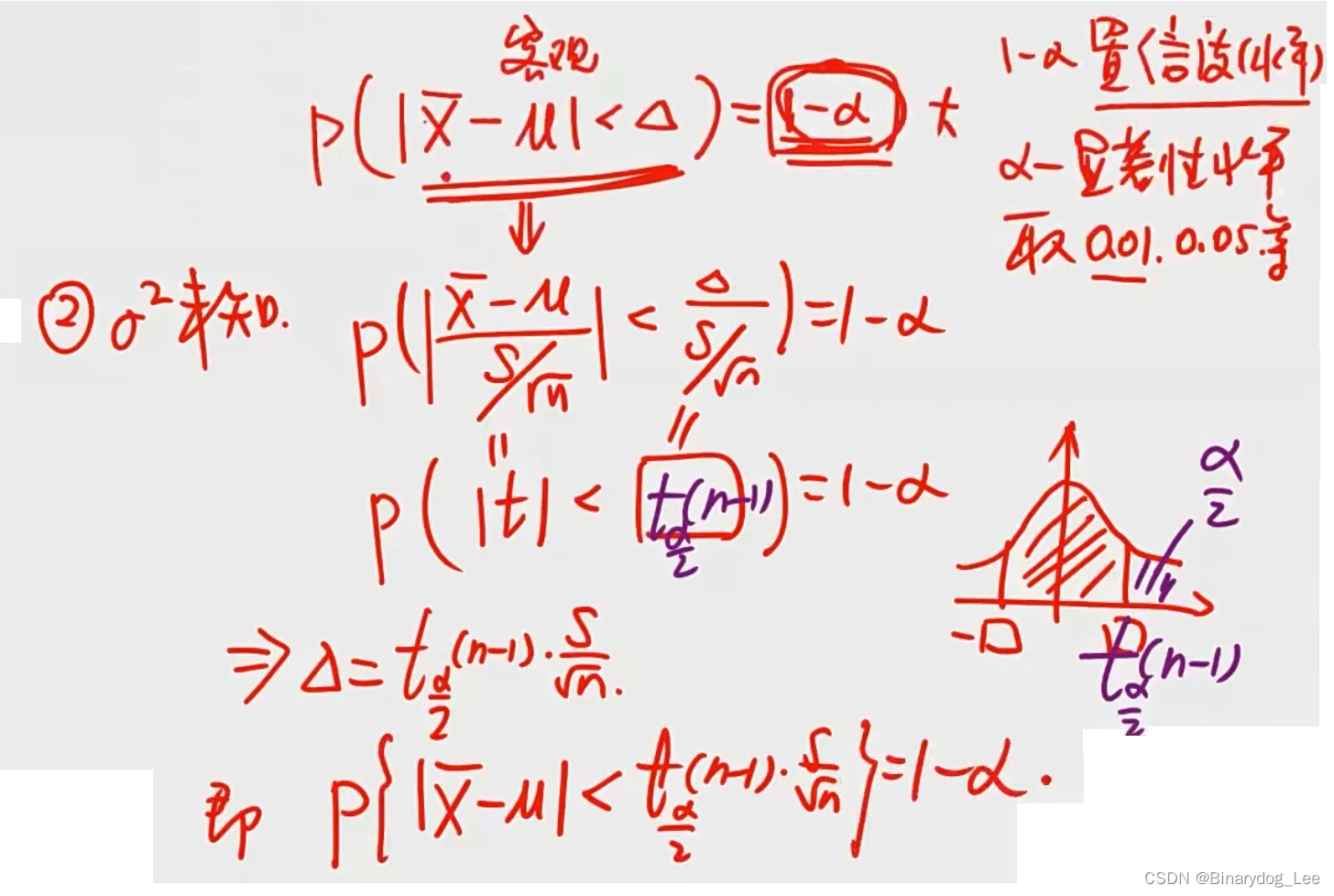
做题先看${\sigma }^2$是否未知，已知用上面①图的公式，未知用上面②图的公式。

1. 找样本容量$n$、样本均值$\overline{x}$等基本参数
2. 明确显著性水平$\alpha$是多少，显然$1-\alpha$即置信区间（若有求的则可套公式出）
3. 找拒绝域就是求$\Delta$（上图有）

拒绝的依据就是事实如何，假设的东西必须适用于事实才行。

显著性水平$\alpha$的意义是原假设$H_0$成立，经检验被拒绝的概率，即 P { 拒绝 H 0 ∣ H 0 为真 } P\{拒绝H_0|H_0为真\} P{拒绝H0​∣H0​为真}，即假设小概率事件不会发生，若发生了（即事实数据落入拒绝域），则拒绝$H_0$。

就比如你在显著性水平为$0.05$下检验$H_0:\mu =9.7,H_1\ne 9.7$，然后算出来$\Delta =0.2132$，那么假设的置信区间是$9.7\pm \Delta$，如果事实（即抽样的结果）是$\overline{x}=10$，那么事实落在假设的置信区间的拒绝域，就拒绝$H_0$

求矩估计量/值

求$\theta$的矩估计量/值

1. 令$\overline{X}=EX$
2. 求出$EX$（显然$EX$含$\theta$）
3. 反解$\overline{X}=EX$得到$\stackrel{ᨈ}{\theta }=f(\overline{X})$

求$\theta$的矩估计量则$\stackrel{ᨈ}{\theta }=f(\overline{X})$，求的是矩估计值则$\stackrel{ᨈ}{\theta }=f(\overline{x})$

上述求$EX$部分按之前的知识处理即可，不论是离散型还是连续性。

最大似然估计：离散情况

对未知参数$\theta$进行估计时，在该参数可能的取值范围$I$内选取使样本观测值概率最大的参数值$\stackrel{ᨈ}{\theta }$作为$\theta$的估计。

对于离散型的分布，每个$X_i$的取值对应的有一个概率$p({\theta }_i)$，有$$L(\theta )=\prod _{i=1}^n[p({\theta }_i){]}^{c_i}$$

其中$c_i$是$X_i$出现的次数，例如$X=3$概率是$1-5\theta$，且样本中$X=3$出现了3回，那就有$(1-5\theta {)}^3$当然也得对其他项这样做，并把结果乘一块。

然后解下式，反解出$\theta =?$
$$\frac{d\ln L(\theta )}{d\theta }=0$$

附录

概率论与数理统计常用公式大全