神经网络解决推荐系统问题（DeepFM，AFM）

最新推荐文章于 2025-02-19 09:18:46 发布

上杉翔二

最新推荐文章于 2025-02-19 09:18:46 发布

阅读量3.9k

点赞数 2

分类专栏：推荐系统文章标签：推荐系统注意力机制 AFM 深度学习 Tensorflow

本文链接：https://blog.csdn.net/qq_39388410/article/details/85119300

版权

推荐系统专栏收录该内容

39 篇文章

订阅专栏

在这里插入图片描述

对于函数的求解大多分为以下几种途径：
确定性求解：通过对数据的规律进行建模直接求解，如特征方程等。
确定性近似求解：通过变分推断的相关方法进行求解，如EM，变分自编码。
随机性近似求解：通过采样的方法对函数进行求解，蒙特卡洛方法。
非结构化求解：DEEP LEARNING.

之所以是非结构化，即是深度神经网络能通过众多的简单线性变换层次性的进行非线性变换对于数据中的复杂关系能够很好的进行拟合，即对数据特征进行的深层次的挖掘，即特性在于能够无限逼近求解。因此作为一种技术手段，深度神经网络对于任何领域都是适用的，这也是这个系列需要学习的东西：通过神经网络来解决推荐系统的问题。

DeepFM
FM+DNN=DeepFM
回顾前一篇的FM，FM可以对高阶特征组合进行建模，但实际上因为计算复杂度的原因一般都只用到了二阶特征组合。那么对于高阶的特征组合来说，我们很自然的想法，通过多层的神经网络即DNN去解决–DeepFM的思想如下。
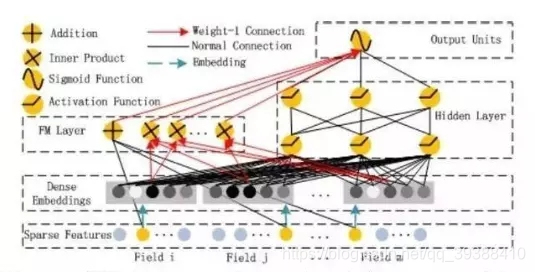
在这里插入图片描述
如图所示，DeepFM采用的是一种并行结构，即它包含了左边的传统FM部分和右边的DNN部分。而且这两部分共享相同的输入，特别是共享了下边的embedding层映射为相同的k维（FM学习到的隐变量），这样可以从原始数据中同时学习到低维与高维特征，而且不再需要特征工程人为设计。一边FM和一边DNN也可以同时学习到高维和低维的特征，效果也是很好的。它的定义的输出为： $y = sigmoid(y_{FM}+y_{DNN})$

embedding代码，下面也需要用到。这里定义它的参数，通过神经网络来进行映射，学习到新的变量。feat_index是特征的一个序号，主要用于通过embedding_lookup选择我们的embedding。feat_value是对应的特征值，如果是离散特征的话，就是1，如果不是离散特征的话，就保留原来的特征值。label是实际值。还定义了两个dropout来防止过拟合。

self.embeddings = tf.nn.embedding_lookup(self.weights['feature_embeddings'],self.feat_index) # N * F * K
feat_value = tf.reshape(self.feat_value,shape=[-1,self.field_size,1])
self.embeddings = tf.multiply(self.embeddings,feat_value) # N * F * K

DeepFM通过把DNN和FM结合，可以从原始特征中同时学习到高阶和低阶的特征交互，所以从图中实际上它就是将FM和DNN模拟的输出相加之后，再整体通过一个Sigmoid作为最后的输出，但是它应用在实际中应用广泛，特征是在排序模块时会有很不错的效果。

AFM
不过有关DNN的结合留到之后详述，而AFM，即是加入了Attention机制的AFM模型，也是一种解决方案。如果对NLP有了解的，应该知道Attention机制其实就相当于一个加权平均。由于因式分解机(FMs)是一种有监督的学习方法，它通过引入二阶特征相互作用来增强线性回归模型。但由于它对具有相同权重的所有特征交互都进行了建模，但是并不是所有的特征交互都具有同等的有用性和预测性（而有些不重要的特征还有可能引入噪音并降低性能），所以AFM就是通过神经网络从数据中学习每个特征交互的重要性用来调整模型。具体架构为：
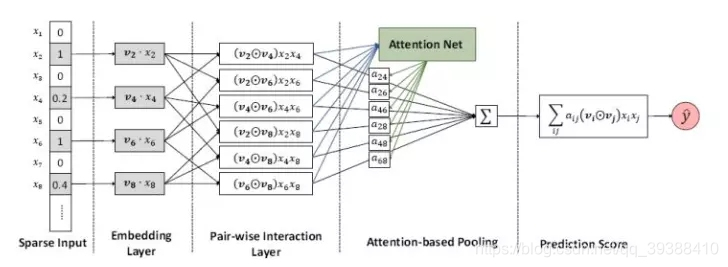
在这里插入图片描述
前面3层的特征组合和FM是一样的，关键在于Attention对于每种不同的组合进行了权重的赋予。

【Attention机制】引自于视觉注意力机制是人类视觉所特有的大脑信号处理机制。我们在看物体的时候会“聚焦”，即重点关注的我们想要的目标区域，然后加以“权重”，获取目标区域里面的细节，得到更好的结果。虽然Attention机制是一种通用的思想，很多方法都可以实现，但目前来说都是基于Encoder-Decoder框架下进行处理，即自动编码机，只是我们对中间的h进行调整。
在这里插入图片描述
然后通过不断的映射调整，训练以得到我们需要的“权重”。预测y值就变为：

其中圆点就是他们之间的特征组合。

if self.attention:#定义权重
   glorot = np.sqrt(2.0 / (self.hidden_factor[0]+self.hidden_factor[1]))
   all_weights['attention_W'] = tf.Variable(
       np.random.normal(loc=0, scale=glorot, size=(self.hidden_factor[1], self.hidden_factor[0])), dtype=np.float32, name="attention_W")  # K * AK
       
   all_weights['attention_b'] = tf.Variable(
       np.random.normal(loc=0, scale=glorot, size=(1, self.hidden_factor[0])), dtype=np.float32, name="attention_b")  # 1 * AK
       
   all_weights['attention_p'] = tf.Variable(
       np.random.normal(loc=0, scale=1, size=(self.hidden_factor[0])), dtype=np.float32, name="attention_p") # AK

一步一步的计算Attention：
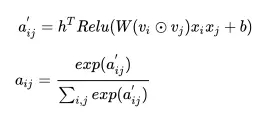
在这里插入图片描述

def _init_graph(self):
        '''
        初始化计算图
        '''
        self.graph = tf.Graph()
        with self.graph.as_default():  # , tf.device('/cpu:0'):
            #设置图的随机种子
            tf.set_random_seed(self.random_seed)
            #输入数据。主要是features和labels。None是批次数目，features_M是数据集有的特征one-hot维度
            self.train_features = tf.placeholder(tf.int32, shape=[None, None], name="train_features_afm")  # None * features_M
            self.train_labels = tf.placeholder(tf.float32, shape=[None, 1], name="train_labels_afm")  # None * 1
            self.dropout_keep = tf.placeholder(tf.float32, shape=[None], name="dropout_keep_afm")
            self.train_phase = tf.placeholder(tf.bool, name="train_phase_afm")

            #初始化变量权重
            self.weights = self._initialize_weights()

            #模型part
            #先嵌入
            self.nonzero_embeddings = tf.nn.embedding_lookup(self.weights['feature_embeddings'], self.train_features) # None * M' * K，嵌入维度是K，M'为field size

            #对特征两两组合，再相乘。
            element_wise_product_list = []
            count = 0
            for i in range(0, self.valid_dimension):#用2层for实现组合
                for j in range(i+1, self.valid_dimension):
                    element_wise_product_list.append(tf.multiply(self.nonzero_embeddings[:,i,:], self.nonzero_embeddings[:,j,:]))#再相乘
                    count += 1
            self.element_wise_product = tf.stack(element_wise_product_list) # (M'*(M'-1)) * None * K，一共(M'*(M'-1))对组合
            self.element_wise_product = tf.transpose(self.element_wise_product, perm=[1,0,2], name="element_wise_product") # None * (M'*(M'-1)) * K，调整一下维度
            self.interactions = tf.reduce_sum(self.element_wise_product, 2, name="interactions")#再求和
            # _________ MLP Layer / attention part _____________
            #开始计算Attention部分。按照公式首先算h^T Relu((W v_iv_jx_ix_j)+b)，再softmax的都分数，最后再回乘为每个组合的重要性进行加权。
            num_interactions = self.valid_dimension*(self.valid_dimension-1)/2#总的组合数，因为内层是从i+1开始的，可以理解为矩阵的一半
            if self.attention:
                self.attention_mul = tf.reshape(tf.matmul(tf.reshape(self.element_wise_product, shape=[-1, self.hidden_factor[1]]), \
                    self.weights['attention_W']), shape=[-1, num_interactions, self.hidden_factor[0]])#先算(W v_iv_jx_ix_j)+b
                # self.attention_exp = tf.exp(tf.reduce_sum(tf.multiply(self.weights['attention_p'], tf.nn.relu(self.attention_mul + \
                #     self.weights['attention_b'])), 2, keep_dims=True)) # None * (M'*(M'-1)) * 1
                # self.attention_sum = tf.reduce_sum(self.attention_exp, 1, keep_dims=True) # None * 1 * 1
                # self.attention_out = tf.div(self.attention_exp, self.attention_sum, name="attention_out") # None * (M'*(M'-1)) * 1
                self.attention_relu = tf.reduce_sum(tf.multiply(self.weights['attention_p'], tf.nn.relu(self.attention_mul + \
                    self.weights['attention_b'])), 2, keep_dims=True) # None * (M'*(M'-1)) * 1，进行Relu
                self.attention_out = tf.nn.softmax(self.attention_relu)#再softmax得到分数
                self.attention_out = tf.nn.dropout(self.attention_out, self.dropout_keep[0]) # dropout
            
            # _________ Attention-aware Pairwise Interaction Layer _____________
            if self.attention:#用分数给element_wise_product即组合进行加权
                self.AFM = tf.reduce_sum(tf.multiply(self.attention_out, self.element_wise_product), 1, name="afm") # None * K
            else:#如果不用注意力加权就是element_wise_product本身
                self.AFM = tf.reduce_sum(self.element_wise_product, 1, name="afm") # None * K
            #算AFM_FM是为了论文中的微观分析。
            self.AFM_FM = tf.reduce_sum(self.element_wise_product, 1, name="afm_fm") # None * K
            self.AFM_FM = self.AFM_FM / num_interactions
            self.AFM = tf.nn.dropout(self.AFM, self.dropout_keep[1]) # dropout

            # _________ out _____________
            #得到预测的输出，除了二次项，还需要计算偏置项w0和一次项\sum w_ix_i
            if self.micro_level_analysis:#微观分析对比两种变体。
                self.out = tf.reduce_sum(self.AFM, 1, keep_dims=True, name="out_afm")
                self.out_fm = tf.reduce_sum(self.AFM_FM, 1, keep_dims=True, name="out_fm")
            else:
                self.prediction = tf.matmul(self.AFM, self.weights['prediction']) # None * 1
                Bilinear = tf.reduce_sum(self.prediction, 1, keep_dims=True)  # None * 1
                self.Feature_bias = tf.reduce_sum(tf.nn.embedding_lookup(self.weights['feature_bias'], self.train_features) , 1)  # None * 1
                Bias = self.weights['bias'] * tf.ones_like(self.train_labels)  # None * 1
                #FM的输出最后由三部分组成二次，一次，偏置
                self.out = tf.add_n([Bilinear, self.Feature_bias, Bias], name="out_afm")  # None * 1

            #计算损失函数。
            if self.attention and self.lamda_attention > 0:
                self.loss = tf.nn.l2_loss(tf.subtract(self.train_labels, self.out)) + tf.contrib.layers.l2_regularizer(self.lamda_attention)(self.weights['attention_W'])  # regulizer
            else:
                self.loss = tf.nn.l2_loss(tf.subtract(self.train_labels, self.out))

            #多种梯度下降优化器
            if self.optimizer_type == 'AdamOptimizer':
                self.optimizer = tf.train.AdamOptimizer(learning_rate=self.learning_rate, beta1=0.9, beta2=0.999, epsilon=1e-8).minimize(self.loss)
            elif self.optimizer_type == 'AdagradOptimizer':
                self.optimizer = tf.train.AdagradOptimizer(learning_rate=self.learning_rate, initial_accumulator_value=1e-8).minimize(self.loss)
            elif self.optimizer_type == 'GradientDescentOptimizer':
                self.optimizer = tf.train.GradientDescentOptimizer(learning_rate=self.learning_rate).minimize(self.loss)
            elif self.optimizer_type == 'MomentumOptimizer':
                self.optimizer = tf.train.MomentumOptimizer(learning_rate=self.learning_rate, momentum=0.95).minimize(self.loss)

            #初始化图
            self.saver = tf.train.Saver()#Saver管理参数便于保存和读取
            init = tf.global_variables_initializer()#初始化模型参数，即run了所有global Variable的assign op。
            self.sess = tf.Session()#会话控制和输出
            self.sess.run(init)#然后运行图

            #计算整个模型的参数数量，这主要是为了证明AFM比其他并行神经网络拥有更少的参数量。
            total_parameters = 0
            for variable in self.weights.values():
                shape = variable.get_shape() #每个参数变量的维度大小
                variable_parameters = 1
                for dim in shape:#所有维度的数量
                    variable_parameters *= dim.value
                total_parameters += variable_parameters
            if self.verbose > 0:
                print "#params: %d" %total_parameters

完整代码的逐行源码阅读笔记在：https://github.com/nakaizura/Source-Code-Notebook/tree/master/AFM

总之AFM衡量特征组合的权重，不仅提高了FM模型的表现能力，而且Attention天生的可解释性能够提高模型的可解释性。然后这只是推荐系统通向更Deep Learning的一小步。