ET算法【基础数论】

ov0_

已于 2024-09-11 16:53:18 修改

阅读量829

点赞数 12

分类专栏： ET基础算法文章标签：算法 c++ 数据结构

于 2024-02-17 17:08:36 首次发布

本文链接：https://blog.csdn.net/qq_39530733/article/details/136112350

版权

ET基础算法专栏收录该内容

9 篇文章 0 订阅

订阅专栏

一、今日有一小段话

寒假过完了....放了一周多的样子....eee。今天是2.14，一个和我没有一毛钱关系的节日，开学了...依稀记得去年这时候，我还在金太阳联考呢www。

二、因数与质因数

1.因数

P1001 - 【模板】求N的所有因子 - ETOJ (eriktse.com)

假设 N = a * b （a <= b），则有 a <= $\sqrt{N}$ <= b，所以只需要枚举1到 $\sqrt{N}$ 即可

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int main() {
	ll n; cin >> n;
	vector<ll> v;
	for(ll i = 1; i * i <= n; i++){
		if(n % i) continue;
		v.push_back(i);
		if(i != n / i) v.push_back(n / i);
	}
	sort(v.begin(), v.end());
	for(auto &i : v) cout << i << ' ';
}

2.质因数

P1002 - 【模板】求N的所有质因子 - ETOJ (eriktse.com)

得到一个因数后，用while将n中所有的该因数都除掉即可，最后别忘判断n自身是不是质因数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int main() {
	ll n; cin >> n;
	vector<ll> v;
	for(ll i = 2; i * i <= n; i++){
		if(n % i) continue;
		v.push_back(i);
		while(n % i == 0) n /= i;
	}
	if(n > 1) v.push_back(n);
	for(auto &i : v) cout << i << ' ';
}

三、质数

1.判断质数O(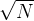 $\sqrt{N}$ )

bool isprime(int n){
    if(n < 2) return false;
    for(int i = 2; i * i <= n; i++){
        if(n % i == 0) return false;
    } 
    return true;
}

2.埃氏筛法O(nloglogn)

P1064 - 【模板】埃氏筛法 - ETOJ (eriktse.com)

如果i是质数，则把i的倍数都标记为非质数

#include<bits/stdc++.h>
using namespace std;

const int N = 2e6 + 10;
bitset<N> vis;
int main() {
	int n; cin >> n;
	vis[1] = true;
	for(int i = 2; i * i <= n; i++){
		if(!vis[i]){
			for(int j = 2 * i; j <= n; j += i){
				vis[j] = true;
			}
		}
	}
	for(int i = 1; i <= n; i++) if(!vis[i]) cout << i <<' ';
}

3.欧拉O(n)

设一个质数数组，将判断为质数的数都放进去，之后再将新遍历到的数乘以质数数组中的质数得到的倍数标为非质数，注意break条件进一步减少重复运算

#include<bits/stdc++.h>
using namespace std;

const int N = 2e6 + 10;
bitset<N> vis;
int prime[N];

int main() {
	int n; cin >> n;
	int cnt = 0;
	vis[1] = true;
	for(int i = 2; i <= n; i++){
		if(!vis[i]) prime[++cnt] = i;
		for(int j = 1; j <= cnt && i * prime[j] <= n; j++){
			vis[i * prime[j]] = true;
			if(i % prime[j] == 0) break; 
		}
	}
	for(int i = 1; i <= n; i++) if(!vis[i]) cout << i << ' ';
}

四、最大公约数和最小公倍数

P1051 - 【模板】gcd和lcm - ETOJ (eriktse.com)

使用库函数__gcd(a, b)即可， a * b = __gcd(a, b) * lcm(a, b);

1.gcd(x, y) = gcd(x, y-x) (x < y)

Problem - 1458A - Codeforces

int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= m; i++) cin >> b[i];
sort(a + 1, a + 1 + n);
for(int i = 1; i <= n - 1; i++){
	d[i] = a[i + 1] - a[i]; 
}
int x = d[1];
for(int i = 2; i <= n - 1; i++){
	x = __gcd(x, d[i]);
}
for(int i = 1; i <= m; i++){
	cout << __gcd(a[1] + b[i], x) << ' ';
}

五、快速幂

P1047 - 【模板】快速幂 - ETOJ (eriktse.com)

倍增思想

#include<bits/stdc++.h>
using namespace std;
#define qio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
typedef long long ll;

ll qpow(ll a, ll b, ll c){
	ll res = 1;
	while(b){
		if(b & 1) res = res * a % c; 
		a = a * a % c;
		b >>= 1;
	}
	return res;
}

int main() {
	int t; cin >> t;
	while(t--){
		ll a, b, c; cin >> a >> b >> c;
		cout << qpow(a, b, c) << '\n';
	}	
}

六、乘法逆元

如果 $(\frac{b}{a})$ % p = x ，那么 b % p = ( x * a ) % p

如果 $(\frac{1}{a})$ % p = x ，那么 ( x * a ) % p = 1 ，x即为a的逆元（在模p意义下）

$(\frac{a\times b}{c})$ % p = ( a * b * inv(c)) % p inv(c)为c的逆元

inv(c) 由费马小定理（或欧拉定理）求解 inv(c) = $(\frac{1}{c})$ % p = $c^{p-2}$ % p

P1063 - 【模板】乘法逆元 - ETOJ (eriktse.com)

#include<bits/stdc++.h>
using namespace std;
#define qio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
typedef long long ll;

const int mod = 998244353;

ll qpow(ll a, ll b){
	ll res = 1;
	while(b){
		if(b & 1) res = res * a % mod; 
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

ll inv(ll x){
	return qpow(x, mod - 2);
}

ll f(ll a, ll b, ll c, ll x){
	return (a * x % mod + b) % mod * inv(c * x % mod) % mod; 
}

int main() {
	int t; cin >> t;
	while(t--){
		ll a, b, c, q; cin >> a >> b >> c >> q;
		while(q--){
			ll x; cin >> x;
			cout << f(a, b, c, x) << '\n';
		}
	}	
}

七、组合数

1.计算组合数 $_{n}^{m}\textrm{C} = _{n - 1}^{m -1}\textrm{C} + _{n -1}^{m}\textrm{C}$

P1065 - 求组合数（1） - ETOJ (eriktse.com)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 1e3 + 10;
const int p = 1e9 + 7;
ll c[N][N];

int main() {
	int n, m; cin >> n >> m;
	for(int i = 0; i < n; i++) c[i][0] = 1ll;	
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= i && j < m; j++){
			c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % p;
		}
	}
	for(int i = 0; i < n; i++){
		for(int j = 0; j < m; j++){
			cout << c[i][j] << " \n"[j == m - 1];
		}
	}
}

2.公式计算

P1066 - 求组合数（2） - ETOJ (eriktse.com)

#include<bits/stdc++.h>
using namespace std;
#define qio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
typedef long long ll;

const int N = 1e7 + 10;
const int p = 1e9 + 7;

ll fac[N];

void init(){
	fac[0] = 1;
	for(int i = 1; i <= N; i++) fac[i] = fac[i - 1] * i % p;
}

ll qpow(ll a, ll b){
	ll res = 1;
	while(b){
		if(b & 1) res = res * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return res;
}

ll inv(ll x){
	return qpow(x, p - 2);
}

ll C(ll n, ll m){
	return fac[n] * inv(fac[n - m] * fac[m] % p) % p;
}

void solve() {
	int n, m; cin >> n >> m;
	cout << C(n, m) << '\n';
}

signed main() {
	qio
	int T = 1;
	cin >> T;
	init();
	while (T--)solve();
}