从零开始编写自己的 C++ 软渲染器（一） 线与三角形的绘制

所谓软渲染器就是使用 CPU 渲染 3D 模型的程序。通常我们编程时调用不到 GPU，学习时的一些实验玩法其实用 CPU 也足够，写一个软渲染器是个很好的乱搞路子学习方法。

前置技能：

C++ 基础

线性代数

四月份的时候曾依葫芦画瓢写过一个很烂的软渲，参考了以下内容：

GAMES 101

tinyrenderer

其一是最近两年图形学领域非常热门的一个入门网课，很多地方值得暂停做笔记思考。不过个人觉得网课如果不写作业交作业的话学起来会感觉很宽泛，做不到面面俱到，难以仔细消化。

与之相对应的 Tinyrenderer 是 github 上一个很有名的仓库，手把手教我们搭建一个自己的软渲染器。我自己的软渲大体就是依照这个项目写的。它的教程英语用语也比较通俗易懂，其实也是非常适合在了解一些图形学基本内容后作为参考的。（不过其内有一些实现是错误的）

我初入图形学时写的一个软渲：

Eykenis/KERenderer: My first attempt to build my own software renderer (github.com)

实现了以下功能：

• 深度测试
• 透视投影
• Flat Shading
• Gouraud Shading
• Phong Shading
• Z-Buffering
• 背面剔除
• 高光以及 Blinn 光照方法
• 单张UV纹理渲染

但还有太多工作没做了。当时其实很多概念都摸不着头脑，边学边写~~（抄）~~，最后的代码就非常难维护。

所以我现在打算重新写一个，尝试把代码维护得更优雅一点。（可能写着写着就烂了）顺便也在这里记下自己对基础知识的复习笔记。

我尽量做一个跨平台的软渲染器，再次实现各种经验光照模型，并做好相机系统（轨道相机和 FPS 相机）。除此以外还有一些有趣的东西（法线/高度图，RampTex，PBR…）。

那么从新建项目并画线开始吧。

新建项目

编译啥的不是我们关心的，还是交给 Visual Studio 来做吧。

Windows GDI 又不熟练了，要不我们用 graphics.h 库吧…

graphics 库的文档可以查 https://docs.easyx.cn/zh-cn/intro。虽然这个 API 比较原始，但在我们的小玩具中用一用是无妨的。

（本文不再对引用 graphics.h 中的函数做注释）

再随便取个项目名字。

好了，现在 initgraph，得到一个空窗口~

我们先设置窗口为 800x600 吧。

想想接下来要做什么。

Bresenham 画线法

如果我们现在可以选择改变屏幕上某个像素的颜色，那么如何画一条线呢？

先说一下自己 yy 的一个朴素的想法。

我们不妨确定两个点，然后一步一步走过来。

我们可以认为一条线是从起点 $A$ 指向终点$B$ 的向量 $\mathbf{v}$. 然后我们计算这两个点的像素距离 $dis$，然后写出以下代码：

void drawLine(double x0, double y0, double x1, double y1, int color) {
	double vx = x1 - x0, vy = y1 - y0;
	double dis = sqrt(vy * vy + vx * vx);
	double wx = x0, wy = y0;
	vx /= dis, vy /= dis;
	for (int i = 0; i < dis; ++i) {
		putpixel(wx, wy, color);
		wx += vx;
		wy += vy;
	}
}

那么这个朴素的矢量画线法我测试了很多不同方向得到的结果都和 Bresenham 画线法是一样的，其实够用了。。

不过还是复习一下 Bresenham，毕竟其还可以拓展出画圆，画各种弧度的方法，更有效。

Bresenham 的思想是：给定两个坐标，我们所连接的线是我们假想的矢量，但光栅化的条件下，我们只能在各个整数点一个像素一个像素的画。那么当矢量线经过某个整横坐标点时 $(x\in \mathbb{Z})$，若它的纵坐标是 $y$，离它最近的两个纵坐标是 $y_1,y_2$，那么我们通过四舍五入的方法决定是画 $(x,y_1)$ 还是 $(x,y_2)$.

如果我们只考虑第一象限的情况：当我们画了 $(x,y)$ 后，我们要确定下一个点是画 $(x+1,y)$ 还是 $(x+1,y+1)$.

但如果这个线的斜率绝对值大于 $1$ 的话，我们就要交换坐标轴，反过来考虑，在整数的纵坐标决定画 $(x_1,y)$ 或 $(x_2,y)$

这样我们就能覆盖所有倾斜角的情况了。

其实还有比较重要的一点，Bresenham 的实现是可以不需要浮点数的（

void drawLine(int x0, int y0, int x1, int y1, int color) {
    int dx = abs(x1 - x0);
    int dy = abs(y1 - y0);
    int gx = x0 < x1 ? 1 : -1;
    int gy = y0 < y1 ? 1 : -1;
    int p = (dx > dy ? dx : -dy) / 2;
    while (!(x0 == x1 && y0 == y1)) {
        putpixel(x0, y0, color);
        int tmp = p;
        if (tmp > -dx) p -= dy, x0 += gx;
        if (tmp < dy)  p += dx, y0 += gy;
    }
    putpixel(x0, y0, color);
}

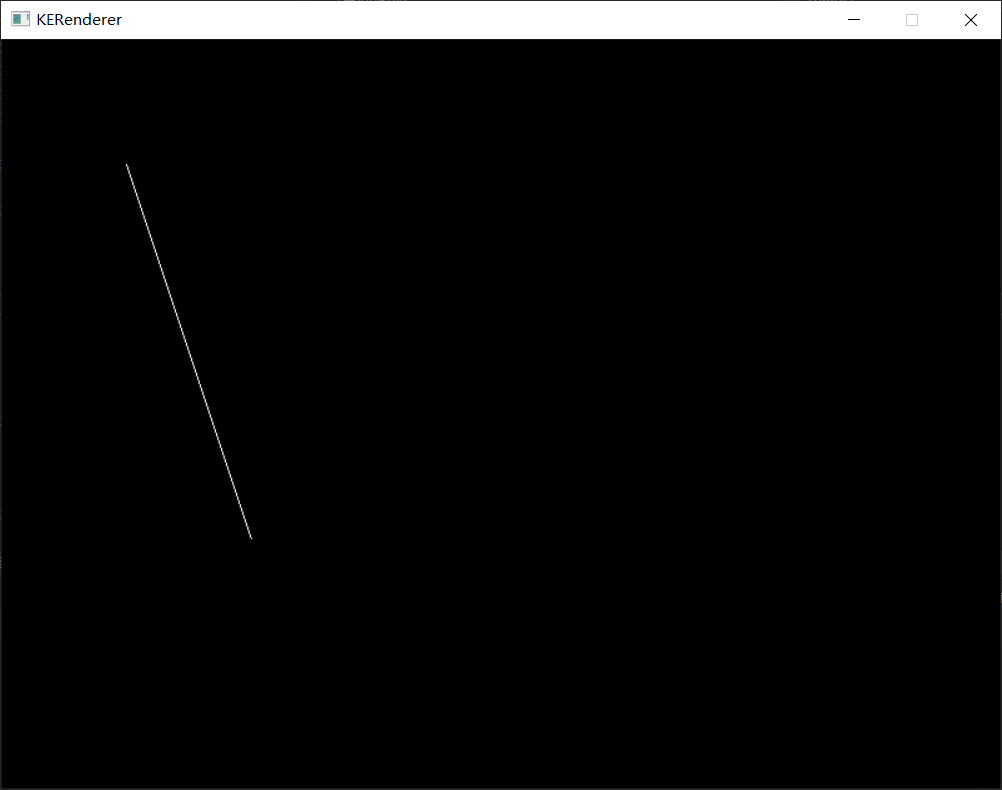
总之，我们得到一个画线的方法，然后在屏幕上调用 drawLine(100, 100, 200, 0xffffff) 试试：

三角形

首先是线框三角形，实现起来很简单，只需要依次调用三次 drawLine 即可，就不写了。

我们来讨论如何光栅化一个实心的三角形。

先说一下最朴素的方法。首先取出三角形的 $x$ 轴和 $y$ 轴边界，得到一个包围三角形的矩形（一般我们称其为这个三角形的 bounding box, 碰撞箱）。然后遍历矩形内的所有点，判断每个点是否在三角形内，如果是就画点。

判断点是否在三角形内，考虑向量叉乘，给定一个线段的两端点 $A,B$ 和另一点 $P$，我们只需要判断 $\overrightarrow{BA}\times \overrightarrow{BP}$ 的方向（符号），即可知道点 $P$ 在直线的哪一边。

那么我们逆时针，或者顺时针枚举出三角形的全部三个向量 $\overrightarrow{BA},\overrightarrow{AC},\overrightarrow{CB}$，当且仅当 $\overrightarrow{BA}\times \overrightarrow{BP},\overrightarrow{AC}\times \overrightarrow{AP},\overrightarrow{CB}\times \overrightarrow{CP}$ 的符号全相等时，$P$ 在三角形 $ABC$ 内。

如果其中有一个值为 $0$，说明点在三角形上。

先打住。 到这里我们发现，向量是经常要用到的，为了方便后面的编写，提高代码可读性，应该写一个数学库，对象化向量。后面需要变换时，我们还会用上矩阵。所以实现一个数学库用于矩阵与向量计算。可以尝试自己实现，或者也可以使用网上的一些库（例如 GLM）。

我这里自己实现了一个 kmath 命名空间，实现线性代数的运算。目前的实现是这样的，之后每次有更新都会说明。

// kmath.h
#pragma once
#include <cmath>
#define vec2i vec2<int>
#define vec2f vec2<float>
#define vec3i vec3<int>
#define vec3f vec3<float>

namespace kmath {
	template<typename T> struct vec2 {
		union {
			struct {
				T x, y;
			};
			struct {
				T u, v;
			};
			T a[2];
		};

		vec2<T>() {
			x = y = 0;
		}
		~vec2<T>() { }
		vec2<T>(T _x, T _y) {
			x = _x;
			y = _y;
		}
		vec2<T>(const vec2<T>& v) {
			x = v.x;
			y = v.y;
		}

		T operator * (const vec2<T>& v) {
			return this->x * v.x + this->y * v.y;
		}

		vec2<T> operator + (const vec2<T>& v) {
			return vec2(this->x + v.x, this->y + v.y);
		}

		vec2<T> operator - (const vec2<T>& v) {
			return vec2(this->x - v.x, this->y - v.y);
		}

		vec2<T> operator * (const T t) {
			return vec2(this->x * t, this->y * t);
		}

		vec2<T>& operator = (const vec2<T>& v) {
			this->x = v.x; this->y = v.y;
			return *this;
		}
	};

	template<typename T> struct vec3 {
		union {
			struct {
				T x, y, z;
			};
			struct {
				T r, g, b;
			};
			T a[3];
		};

		vec3<T>() {
			x = y = z = 0;
		}
		~vec3<T>() { }
		vec3<T>(T _x, T _y, T _z) {
			x = _x;
			y = _y;
			z = _z;
		}
		vec3<T>(const vec3<T>& v) {
			x = v.x;
			y = v.y;
			z = v.z;
		}

		T operator * (const vec3<T>& v) {
			return this->x * v.x + this->y * v.y + this->z * v.z;
		}

		vec3<T> operator + (const vec3<T>& v) {
			return vec3<T>(this->x + v.x, this->y + v.y, this->z + v.z);
		}

		vec3<T> operator - (const vec3<T>& v) {
			return vec3<T>(this->x - v.x, this->y - v.y, this->z - v.z);
		}

		vec3<T> operator * (const T t) {
			return vec3<T>(this->x * t, this->y * t, this->z * t);
		}

		vec3<T>& operator = (const vec3<T>& v) {
			this->x = v.x; this->y = v.y; this->z = v.z;
			return *this;
		}
	};
	template<typename T> T cross(const vec2<T>& u, const vec2<T>& v) {
		return u.x * v.y - u.y * v.x;
	}
	template<typename T> vec3<T> cross(const vec3<T>& u, const vec3<T>& v) {
		return vec3<T>(u.y * v.z - u.z * v.y, u.z * v.x - u.x * v.z, u.x * v.y - u.y * v.x);
	}
};

那么我们依靠其写出一个判断点是否在三角形内的 check 函数：

bool inTriangle(int x1, int y1, int x2, int y2, int x3, int y3, int xp, int yp) {
    kmath::vec2<int> v1(x2 - x1, y2 - y1), v2(x3 - x2, y3 - y2), v3(x1 - x3, y1 - y3);
    kmath::vec2<int> p1(xp - x1, yp - y1), p2(xp - x2, yp - y2), p3(xp - x3, yp - y3);
    int r1 = cross(v1, p1), r2 = cross(v2, p2), r3 = cross(v3, p3);
    if (!r1 || !r2 || !r3) return true;
    if (r1 > 0 && r2 > 0 && r3 > 0) return true;
    if (r1 < 0 && r2 < 0 && r3 < 0) return true;
    return false;
}

然后，我们在三角形光栅化的函数中遍历整个 bounding box ，判断像素点是否在三角形内来决定是否绘制这个像素点，就可以啦

void drawTriangle(int x1, int y1, int x2, int y2, int x3, int y3, int color) {
    int lx = min(x1, min(x2, x3)), rx = max(x1, max(x2, x3));
    int dy = min(y1, min(y2, y3)), uy = max(y1, max(y2, y3));
    for (int i = lx; i <= rx; ++i) {
        for (int j = dy; j <= uy; ++j) {
            if (inTriangle(x1, y1, x2, y2, x3, y3, i, j)) {
                putpixel(i, j, color);
            }
        }
    }
}

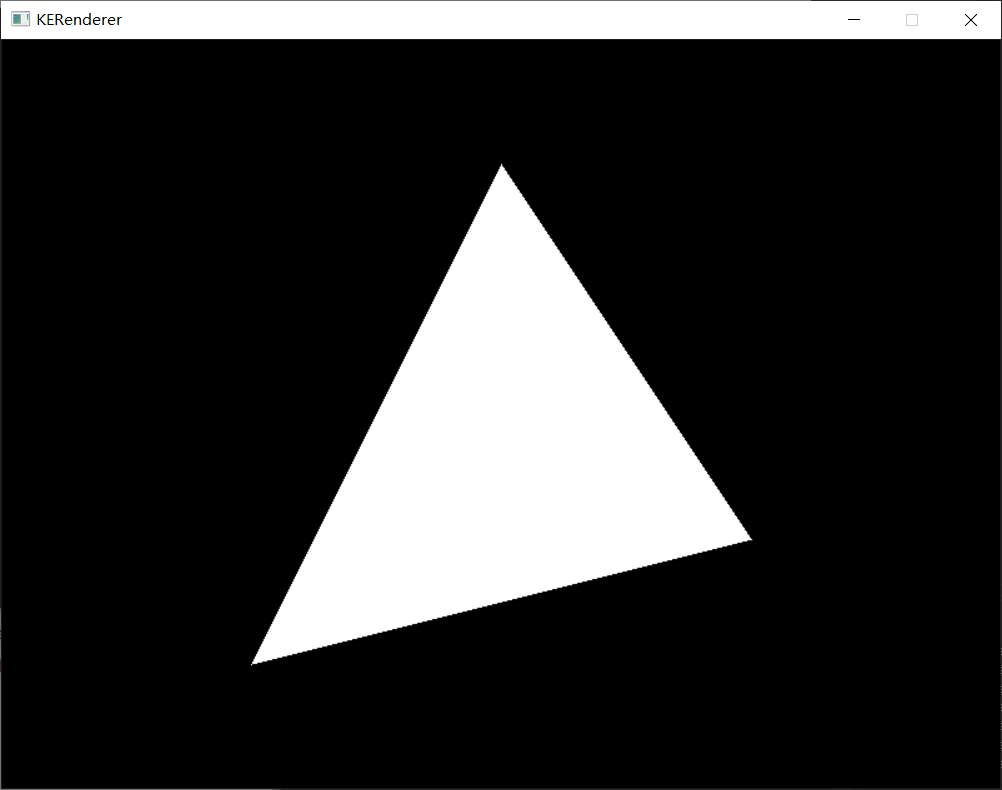
在主程序中调用 drawTriangle(400, 100, 200, 500, 600, 400, 0xffffff)，得到如下结果：