零基础学习(凸优化)
凸优化学习视频:https://www.bilibili.com/video/BV16W411f7Y7?p=4
凸优化主要内容
一、凸集
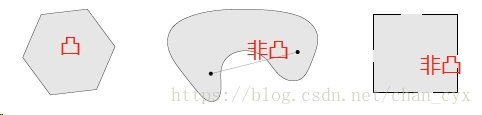
集合C内任意两点间的线段均在集合C内,则称集合C为凸集。
∀
x
1
,
x
2
,
.
.
.
,
x
k
∈
C
,
θ
i
∈
[
0
,
1
]
且
∑
i
=
1
k
θ
i
=
1
,
则
X
=
∑
i
=
1
k
θ
i
x
i
∈
C
\forall x_1,x_2,...,x_k\in C,\theta_i\in[0, 1]且\sum_{i=1}^{k}\theta_i=1,则X=\sum_{i=1}^{k}\theta_ix_i\in C
∀x1,x2,...,xk∈C,θi∈[0,1]且i=1∑kθi=1,则X=i=1∑kθixi∈C
例: x = θ x 1 + ( 1 − θ ) x 2 , θ ∈ ( 0 , 1 ) x=\theta x_1+(1-\theta)x_2 ,\theta\in(0, 1) x=θx1+(1−θ)x2,θ∈(0,1)
- 在凸集C中, x 1 , x 2 ∈ C , 0 ≤ θ ≤ 1 ⇒ θ x 1 + ( 1 − θ ) x 2 ∈ C x_1, x_2\in C, 0\le \theta\le1\Rightarrow\theta x_1+(1-\theta)x_2\in C x1,x2∈C,0≤θ≤1⇒θx1+(1−θ)x2∈C
- 如图
二、凸函数
定义:
若函数f的定义域domf为凸集,且满足
∀x,y ∈ domf,0≤θ≤1,有f(θx + (1-θ)y) ≤ θf(x) + (1-θ)f(y)
则这样的函数f就是凸函数。
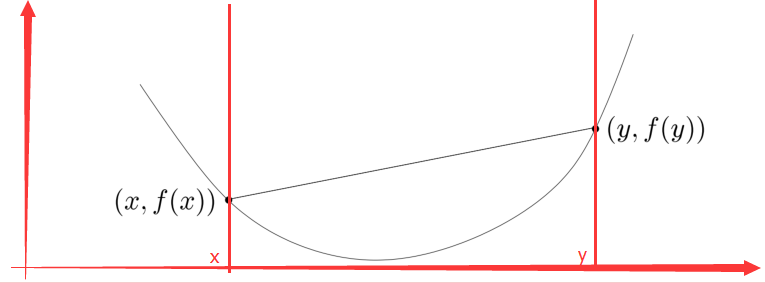
如果一个函数是凸函数,则该函数的图像上方区域一定是凸集。反过来也成立,即:如果一个函数图像的上方区域是凸集,则该函数是凸函数,于是如下图所示:
这个图像就是函数y=x2的图像,这个函数是个在明显不过的凸函数,它的上方区域就是凸集。
三、凸优化
凸优化问题的基本形式:
{ m i n i m i z e f 0 ( x ) , x ∈ R n ( 凸 函 数 ) s u b j e c t t o f i ( x ) ≤ 0 , i = 1 , . . . , m ; ( 凸 函 数 ) h j ( x ) = 0 , j = 1 , . . . , p ; ( 仿 射 函 数 ) \left\{\begin{aligned}minimize & & \ f_0(x), x\in R^n (凸函数)\\subject\ to \ & &f_i(x)\le0,i=1,...,m; (凸函数)\\& &h_j(x)=0,j=1,...,p;(仿射函数)\end{aligned}\right. ⎩⎪⎨⎪⎧minimizesubject to f0(x),x∈Rn(凸函数)fi(x)≤0,i=1,...,m;(凸函数)hj(x)=0,j=1,...,p;(仿射函数)
凸优化问题求解的方式为:求原函数 f 0 ( x ) f_0(x) f0(x)的最小值转化为求Lagrange对偶函数求极大值。
Lagrange乘子法:
求解优化问题一般用Lagrange乘子法。
{
m
i
n
i
m
i
z
e
f
0
(
x
)
,
x
∈
R
n
(
凸
函
数
)
s
u
b
j
e
c
t
t
o
f
i
(
x
)
≤
0
,
i
=
1
,
.
.
.
,
m
;
(
凸
函
数
)
h
j
(
x
)
=
0
,
j
=
1
,
.
.
.
,
p
;
(
仿
射
函
数
)
\left\{\begin{aligned}minimize & & \ f_0(x), x\in R^n (凸函数)\\subject\ to \ & &f_i(x)\le0,i=1,...,m; (凸函数)\\& &h_j(x)=0,j=1,...,p;(仿射函数)\end{aligned}\right.
⎩⎪⎨⎪⎧minimizesubject to f0(x),x∈Rn(凸函数)fi(x)≤0,i=1,...,m;(凸函数)hj(x)=0,j=1,...,p;(仿射函数)
其Lagrange函数为:
L
(
x
,
λ
,
ν
)
=
f
0
(
x
)
+
∑
i
=
1
m
λ
i
f
i
(
x
)
+
∑
j
=
1
p
ν
i
h
j
(
x
)
,
其
中
λ
i
≥
0
,
ν
j
∈
R
L(x, \lambda, \nu) = f_0(x)+\sum_{i=1}^m\lambda_if_i(x)+\sum_{j=1}^p\nu_ih_j(x),其中\lambda_i\ge0,\nu_j\in R
L(x,λ,ν)=f0(x)+i=1∑mλifi(x)+j=1∑pνihj(x),其中λi≥0,νj∈R
Lagrange对偶函数:
g ( λ , ν ) = i n f x ∈ D ( f 0 ( x ) + ∑ i = 1 m λ i f i ( x ) + ∑ i = 1 p ν i h i ( x ) ) g(\lambda,\nu)=\mathop{inf}\limits_{x\in D}(f_0(x)+\sum_{i=1}^m\lambda_if_i(x)+\sum_{i=1}^p\nu_ih_i(x)) g(λ,ν)=x∈Dinf(f0(x)+i=1∑mλifi(x)+i=1∑pνihi(x))
其中inf表示下确界,类似极小值。

原问题是求原函数的最小值,但是原函数有约束条件,于是先将原函数转换为Lagrange函数,即 L ( x , λ ) = f ( x ) + λ g ( x ) L(x,\lambda) = f(x)+\lambda g(x) L(x,λ)=f(x)+λg(x),原问题的本质求法是先对 λ \lambda λ求 L ( x , λ ) L(x,\lambda) L(x,λ)的极大值(即上确界sup),然后对x求极小值(即下确界inf),从而得到原函数的极小值,即 i n f x s u p λ ≥ 0 L ( x , λ ) \mathop{inf}\limits_{x}\mathop{sup}\limits_{\lambda\ge0}L(x, \lambda) xinfλ≥0supL(x,λ)。
但是由于上述这种求法不好求,所以将问题转化为先对 x x x求 L ( x , λ ) L(x,\lambda) L(x,λ)的极小值(即获得 L ( x , λ ) L(x, \lambda) L(x,λ)的下确界),从而得到 L ( x , λ ) L(x, \lambda) L(x,λ)的对偶函数 g ( λ ) g(\lambda) g(λ),然后对 g ( λ ) g(\lambda) g(λ)求极大值来近似原函数的最小值,即 s u p λ ≥ 0 i n f x L ( x , λ ) \mathop{sup}\limits_{\lambda\ge0}\mathop{inf}\limits_{x}L(x, \lambda) λ≥0supxinfL(x,λ)


KKT条件
若要对偶函数的最大值即为原问题的最小值,考虑需要满足的条件:
上式的 g ( λ ∗ , ν ∗ ) g(\lambda^*,\nu^*) g(λ∗,ν∗)就是Lagrange对偶函数,
对偶函数的结果 ≤ \le ≤目标值,为了让 ≤ \le ≤变为 = = =:
- 让第三行的 ≤ \le ≤变为 = = =,需要让 x ∗ x^* x∗是第二行Lagrange函数的驻点,让Lagrange函数对x求偏导的值为0,即 ∇ f 0 ( x ∗ ) + ∑ i = 1 m λ i ∗ ∇ f i ( x ∗ ) + ∑ i = 1 p v i ∗ ∇ h i ( x ∗ ) = 0 \nabla f_0(x^*)+\sum_{i=1}^m\lambda_i^*\nabla f_i(x^*)+\sum_{i=1}^pv_i^*\nabla h_i(x^*)=0 ∇f0(x∗)+∑i=1mλi∗∇fi(x∗)+∑i=1pvi∗∇hi(x∗)=0.
- 为了让第四行的 ≤ \le ≤变为 = = =,需要每个 λ i ∗ f i ( x ∗ ) = 0 \lambda_i^*f_i(x^*)=0 λi∗fi(x∗)=0,因为 λ i ≥ 0 , f i ( x ∗ ) λ_i≥0,f_i(x^*) λi≥0,fi(x∗)是已知的约束条件,是小于等于0的,所有若有一个 λ i ∗ f i ( x ∗ ) ≠ 0 λ_i*f_i(x*)≠0 λi∗fi(x∗)=0,则第三行第二项的值就一定小于0,这样就无法将≤变成=,然后因为hi(x*)是已知的约束条件,是等于0的。
- 加上已知的三个约束条件
所以KKT条件为:
{
∇
f
0
(
x
∗
)
+
∑
i
=
1
m
λ
i
∗
∇
f
i
(
x
∗
)
+
∑
i
=
1
p
v
i
∗
∇
h
i
(
x
∗
)
=
0
(
新
增
的
第
一
个
约
束
)
λ
i
∗
f
i
(
x
∗
)
=
0
(
新
增
的
第
二
个
约
束
)
λ
i
≥
0
(
L
a
g
r
a
n
g
e
乘
子
法
的
定
义
)
f
i
(
x
)
≤
0
(
已
知
的
约
束
条
件
)
h
i
(
x
)
≤
0
(
已
知
的
约
束
条
件
)
其
中
i
=
1
,
2
,
.
.
.
,
m
\left\{\begin{aligned}\nabla f_0(x^*)+\sum_{i=1}^m\lambda_i^*\nabla f_i(x^*)+\sum_{i=1}^pv_i^*\nabla h_i(x^*)=0(新增的第一个约束)\\\lambda_i^*f_i(x^*)=0(新增的第二个约束)\\\lambda_i\ge0(Lagrange乘子法的定义)\\f_i(x)\le0(已知的约束条件)\\h_i(x)\le0(已知的约束条件)\\其中i=1,2,...,m\end{aligned}\right.
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧∇f0(x∗)+i=1∑mλi∗∇fi(x∗)+i=1∑pvi∗∇hi(x∗)=0(新增的第一个约束)λi∗fi(x∗)=0(新增的第二个约束)λi≥0(Lagrange乘子法的定义)fi(x)≤0(已知的约束条件)hi(x)≤0(已知的约束条件)其中i=1,2,...,m
注意:如果原问题中 f i ( x ) f_i(x) fi(x)是凸函数的话,KKT条件是充分条件;如果原问题是个一般性问题,即 f i ( x ) f_i(x) fi(x)不一定是凸函数,则KKT条件是必要条件,不是充分条件。









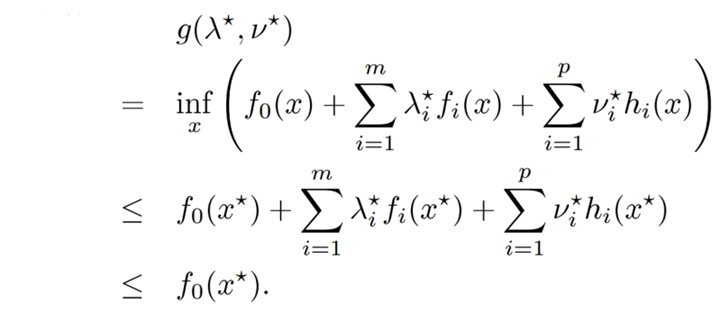














 4176
4176











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








