一. 高斯马尔科夫定理是什么
高斯马尔科夫定理说:对于线性回归模型,在某些约束条件下,由最小二乘法得到的估计量(估计子),即线性回归模型的系数,是最优的线性无偏估计子。也就是说高马解决的问题是线性回归模型,他的作用是给出线性模型的系数估计。
1. 线性回归模型:

其中:
 是
是 的输出列向量(待求的数据);
的输出列向量(待求的数据);
 是
是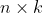 的输入矩阵(测量的数据);
的输入矩阵(测量的数据);
 是
是 的列向量(待求回归系数);
的列向量(待求回归系数);
 是
是 的误差列向量(测量误差)。
的误差列向量(测量误差)。
直观的例子,比如根据学生的英语,数学,物理成绩预测他的地理成绩。高马说,最小二乘法估计的回归系数可以最准确地给出预测。由最小二乘得到的系数估计量为(下次来说为什么)(此时的 和
和 是测量的已知数据。):
是测量的已知数据。):

但是要满足如下的假定 (就是定理中的约束):
(1). 满秩(只有满秩
满秩(只有满秩 才可逆);
才可逆);
(2).误差期望为0:![E[\epsilon|X]=0;](https://i-blog.csdnimg.cn/blog_migrate/61f3ca5326c9a4a6754f2852a011f560.gif)
(3).各向同性协方差矩阵:![Var[\epsilon|X]=\sigma^2I](https://i-blog.csdnimg.cn/blog_migrate/c94408ea665a9e0bb366d03504d7a38f.gif) ;
;
断言: 是最优的线性无偏估计子。
是最优的线性无偏估计子。
这些假定是说,你测量的数据要是满秩的,测量数据的误差期望得是0,误差的协方差得是各向同性的。只有这样,高马才能给出最优的线性无偏估计子。
二. 为什么是他
要说明为什么最小二乘法得到的 是最优的线性无偏估计子,需要说明三个问题,即线性,无偏,最优。
是最优的线性无偏估计子,需要说明三个问题,即线性,无偏,最优。
1.线性性
 关于
关于 是线性的,故线性性得证。
是线性的,故线性性得证。
2.无偏性
无偏即估计量的期望值要和真实的参数值相同。也就是证明: ![E[\hat{\beta}]=\beta](https://i-blog.csdnimg.cn/blog_migrate/0641133a0e353e138a400d9127590e1e.gif)
下面给出 期望值的推导过程。首先,估计量
期望值的推导过程。首先,估计量
 ,
,
根据假定(2),两边同时取条件期望,有
![E[\hat{\beta}|X]=E[\beta|X]+E[(X^TX)^{-1}X^T\epsilon|X]\\ =\beta+(X^TX)^{-1}X^TE[\epsilon|X]\\ =\beta+0\\ =\beta](https://i-blog.csdnimg.cn/blog_migrate/1e10559fb2e56b05f488abb06c2fab10.gif)
利用重期望公式,![E[\hat{\beta}]=E[E[\hat{\beta}|X]]=\beta](https://i-blog.csdnimg.cn/blog_migrate/d7d61001179344a51413427d5265d161.gif) , 从而
, 从而 是无偏估计量。无偏性得证。
是无偏估计量。无偏性得证。
3. 最优性
最优性是说在所有的线性无偏估计子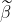 中,
中, 有最小的方差(单变量)或协方差(多元)。因为是多次实验得到的估计量,所以考虑方差是有意义的。
有最小的方差(单变量)或协方差(多元)。因为是多次实验得到的估计量,所以考虑方差是有意义的。
需要证明:![Var[\hat{\beta}|X]\leq Var[\widetilde{\beta}|X]](https://i-blog.csdnimg.cn/blog_migrate/38be0bf48ba65931ed27f595b72c256f.gif) , 即
, 即![Var[\hat{\beta}|X]-Var[\widetilde{\beta}|X]\geq 0](https://i-blog.csdnimg.cn/blog_migrate/2c57df3a9572a5f384758350c2da641d.gif) , 即协方差矩阵(多元)是半正定的。
, 即协方差矩阵(多元)是半正定的。
我们设一般的线性估计子为: 。其中
。其中 是
是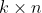 的矩阵。下面来看该估计子的无偏性。
的矩阵。下面来看该估计子的无偏性。
用最小二乘估计子和一般线性估计子作差,即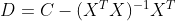 ,那么
,那么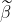 可用最小二乘估计子表示:
可用最小二乘估计子表示: .
.
两边取条件期望:
![E[\widetilde{\beta}|X]=E[Dy+\hat{\beta}|X]\\ =E[Dy|X]+E[\hat{\beta}|X]\\ =E[D(X\beta+\epsilon)|X]+\beta\\ =E[DX\beta|X]+E[D\epsilon|X]+\beta\\ =DXE[\beta|X]+DE[\epsilon|X]+\beta\\ =DX\beta+0+\beta\\ =DX\beta+\beta](https://i-blog.csdnimg.cn/blog_migrate/115f3c5f778f58571cf9f7443a7e0c70.gif)
注意这里 和
和 都是已知的矩阵,因为
都是已知的矩阵,因为 是系数的差,而系数都是常值。
是系数的差,而系数都是常值。 也是已知向量。从期望看出,
也是已知向量。从期望看出,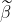 是无偏估计量的充要条件是
是无偏估计量的充要条件是,对任何
 都成立的话,只能
都成立的话,只能。下面来看协方差。
![Var[\hat{\beta}|X]=Var[Dy+\hat{\beta}|X]\\ =Var[D(X\beta+\epsilon)+\hat{\beta}|X]\\ =Var[DX\beta|X]+Var[D\epsilon|X]+Var[\hat{\beta}|X]\\ =0+DVar[\epsilon|X]D^T+Var[\hat{\beta}|X]\\ =\sigma^2DD^T+Var[\hat{\beta}|X]](https://i-blog.csdnimg.cn/blog_migrate/a17ccbd9615c6abb7cef17b352c7544b.gif)
这里用到约束(3):![Var[\epsilon|X]=\sigma^2I](https://i-blog.csdnimg.cn/blog_migrate/c94408ea665a9e0bb366d03504d7a38f.gif) 。那么,
。那么,![Var[\hat{\beta}|X]-Var[\widetilde{\beta}|X]=\sigma^2DD^T](https://i-blog.csdnimg.cn/blog_migrate/f87805463bb8d0ac7df839bfc8329973.gif) ,由
,由 的构造知,
的构造知,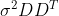 半正定。从而最优性得证。
半正定。从而最优性得证。
























 421
421

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








