如何理解条件平差

最新推荐文章于 2023-08-03 14:10:26 发布

欧阳罢笔

最新推荐文章于 2023-08-03 14:10:26 发布

阅读量9.2k

点赞数 15

分类专栏：平差测量文章标签：条件平差测量平差测绘工程

本文链接：https://blog.csdn.net/qq_39798423/article/details/87091676

版权

平差测量专栏收录该内容

8 篇文章

订阅专栏

为什么要平差，我们知道是因为我们测量的数据（在有多余观测的条件下）产生了矛盾。比如我们测一个三角形，如果只测了两个角，我们知道第三个角一定是180度减前两个角的和。但是如果我们测了三个角，但三个角加起来不等于180度，那就说明测得有误差，我们就需要用一些手段进行平差，消除这些误差
平差最主要的两种是间接平差和条件平差，它们的区别可以参考这里，间接平差使用的比条件平差多得多。简单的说条件平差就是以公理为条件构造条件方程，条件平差不含有独立参数，表示为观测量的隐函数形式，再使用最小二乘即可。但是方程的公理性质不容易找齐，而且这些公理之间必须是互相独立的，要保证列出的方程组无关，所以使用起来比较不容易列齐条件方程。而间接平差是先建立近似的模型，然后来找到真正的模型与近似模型间的改正数，使其平方和最小即可
还是以一个题来说，这是学校平差课的实验题，现在看着当年写的报告，不知道写的什么**玩意儿，只能重新思考了

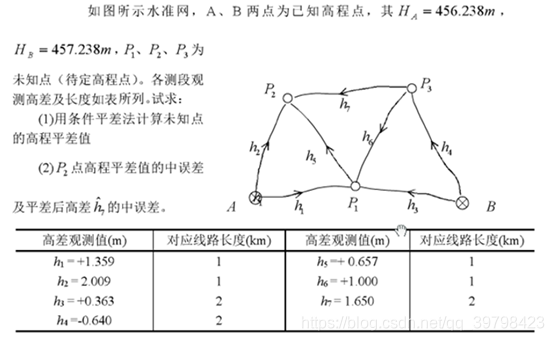
如题（就看第一个问就行了）

我们看题中要求得 $P_{1}$ 、 $P_{2}$ 和 $P_{3}$ 的高，必要观测只需要3条边的高差观测值，比如由 $P_{1}=H_{A}+h_{1}$ 、 $P_{2}=H_{A}+h_{2}$ 、 $P_{3}=H_{B}+h_{4}$ 只要事实上我们测了 $h_{1}$ 、 $h_{2}$ 和 $h_{3}$ 就行了，但是我们一共测了7条边，所以这里我们的必要观测数 $t = 3$ ，总的观测数 $n = 7$ ，所以我们多余观测数为 $r = n - t = 4$ 。在条件平差中，有多少的多余观测，就需要多少的条件方程，所以这里我们需要4个条件方程
现在我们来看图找公理。最容易想到的是，从一个点出去转一圈回来，高程不变嘛，所以根据此我们应该可以得到下面几个公式是正确的（注意，这些公式要是无关的），但是我们测的数据加起来却不是这样的
$h_{1}-h_{2}+h_{5}=0\\ h_{5}+h_{6}-h_{7}=0\\ h_{3}-h_{6}-h_{4}=0\\ h_{1}-h_{3}+H_{A}-H_{B}=0$
这里我们根据下面两个公式化简一下。这里的第一个公式就是我们上面的条件方程，只是上面是理论的，没有写上加上 $A 0$ 才为零；下面的式子中 $\hat{L}$ 表示改正后的值， $V$ 是改正数，也就是真实值等于测量值加上改正值
$A\hat{L}+A^{0}=0\\ \hat{L}=L+V$
得到了 $A V + W = 0$ ，此即为条件平差的函数模型， $W$ 是之前我们算出的闭合差（也就是走一圈回到原点的高程差，这里让改正数和等于闭合差可以看成这样，比如第一个公式，我们需要 $h_{1}+v_{1}-(h_{2}+v_{2})+h_{5}+v_{5}=0$ ，推出 $v_{1}-v_{2}+v_{5}+(h_{1}-h_{2}+h_{5})=0$ ，我们计算可以得到 $W_{1}=h_{1}-h_{2}+h_{5}=7$ ，其他类似），现在我们按照这个形式列出条件方程（注意，单位是毫米mm）
$v_{1}-v_{2}+v_{5}+7=0\\ v_{5}+v_{6}-v_{7}+7=0\\ v_{3}-v_{6}-v_{4}+3=0\\ v_{1}-v_{3}+H_{A}-H_{B}-4=0$
这下我们就可以开始算了，先把知道的矩阵列出来，首先是 $A$ 和 $W$ 阵，还可以把权阵 $P$ 列出来，根据对应路线的长度，设2km为单位权，得到
$\left[ \begin{matrix} 1 & -1 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 1 & -1\\ 0 & 0 & 1 & -1 & 0 & -1 & 0\\ 1 & 0 & -1 & 0 & 0 & 0 & 0 \end{matrix} \right] W= \left[ \begin{matrix} 7\\ 7\\ 3\\ 4 \end{matrix} \right] \\P= \left[ \begin{matrix} 2 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 2 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 2 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix} \right]$
现在我们的目标依旧没变，使得 $V^{T}PV=min$ ，因为我们使用了条件方程，就像附有条件的间接平差，代价函数 $V^{T}PV$ 限制在了条件之中，所以这里要用到拉格朗日乘子法，得到的新的代价为 $\Phi=V^{T}PV−2K^{T}(AV+W)$ ，同样的我们要将 $\Phi$ 对 $V$ 求导，并等于零，即
$\frac{\partial(\Phi)}{\partial(V)}=2V^{T}P−2K^{T}A=0\\ V=-P^{-1}A^{T}(AP^{-1}A^{T})^{-1}W$
推导的过程可以参考这里，现在我们就可以计算一下了，先输入数据，查看一下数据的维度

A = np.array([[1,-1,0,0,1,0,0],
              [0,0,0,0,1,1,-1],
              [0,0,1,-1,0,-1,0],
              [1,0,-1,0,0,0,0]])
W = np.array([7,7,3,-4]).T.reshape(4,1)
P = np.array([[2,0,0,0,0,0,0],
              [0,2,0,0,0,0,0],
              [0,0,1,0,0,0,0],
              [0,0,0,1,0,0,0],
              [0,0,0,0,2,0,0],
              [0,0,0,0,0,2,0],
              [0,0,0,0,0,0,1]])

print(A.shape)
print(W.shape)
print(P.shape)

这里输出为

(4, 7)
(4, 1)
(7, 7)

好，现在开始写方程计算

Q = np.linalg.inv(P)
Naa = np.dot(np.dot(A, Q), A.T)
K = np.dot(np.linalg.inv(Naa), W)
V = -np.dot(np.dot(Q, A.T), K)
print(V)

得到结果，这里从上到下分别对应 $v_{1}$ 到 $v_{7}$

[[-0.42696629]
 [ 2.7752809 ]
 [-4.42696629]
 [-0.26966292]
 [-3.79775281]
 [-1.15730337]
 [ 2.04494382]]

现在我们改成一下 $h 1$ 、 $h 2$ 和 $h 5$ ，然后再算一下 $h 1 - h 2 + h 5 = 0$ 是否成立 $\hat{h_{1}}=h_{1}+v_{1}=1.358573034\\ \hat{h_{2}}=h_{2}+v_{2}=2.011775281\\ \hat{h_{5}}=h_{5}+v_{h}=0.653202247$
现在计算得到 $h 1 - h 2 + h 5 = 0$ ，对了完毕收工。现在再把这道题的答案算了
$P_{1}=H_{A}+h_{1}+v_{1}=457.596573\\ P_{2}=H_{A}+h_{2}+v_{2}=458.2497753\\ P_{3}=H_{B}+h_{4}+v_{4}=456.5977303$