文章目录
1. 图简介
1.1 图的分类
图分为
- 有向图 (digraph): 即所有边皆有向的图
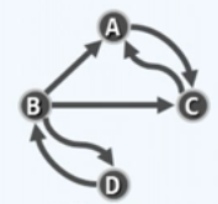
- 无向图 (undigraph): 即所有边皆无向的图
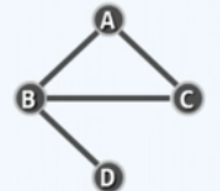
- 混合图(mixed graph): 即含有无向以及有向边的图
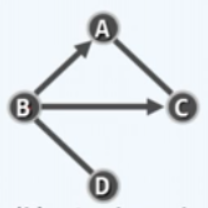
虽然图分为上面三种, 但是我们重点分析有向图, 因为所有的图都可以由有向图简化得到
1.2 图的描述
基于任意一个图都可以由点集V 与边集 E组成 , 我们可以对图 G 做出如下描述
G = ( V ; E ) G = (V;E) G=(V;E)
- V(vertex): V 代表图的点集, 我们令 n = ∣ V ∣ n = |V| n=∣V∣ ,n代表顶点的个数
- E(edge): E 代表图的边集, 我们令 e = ∣ E ∣ e = |E| e=∣E∣, e代表边的个数
1.2.1 边的描述
我们使用 ( u , v ) (u,v) (u,v)来描述一条边
- 若u,v的次序无所谓, 则称为 无向边(undirected edge), 容易看出,所有边均无方向即为无向图
- 若u,v的次序需要考虑,则(u,v)称为有向边(directed edge)
- u为边 ( u , v ) (u,v) (u,v)的尾(tail)
- v为边 ( u , v ) (u,v) (u,v)的头(head)
1.2.2 路径(path)/环路(circle)
路径描述
所谓路径, 就是我们所说的路径, 它由有向边构成, 所以我们可以做出如下的数学描述, 一条路径可以由k个顶点的有序序列描述 ,
v
0
v_0
v0 为路径的起点,
v
k
v_k
vk为路径的终点
路
径
π
=
<
v
0
,
v
1
,
.
.
.
,
v
k
>
长
度
∣
π
∣
=
k
路径\pi = <v_0, v_1, ...,v_k>\\ 长度|\pi| = k
路径π=<v0,v1,...,vk>长度∣π∣=k
路径分类
- path:
- simple path:即没有重复节点的路径, 即不存在 i j , 使得 v i = v j v_i = v_j vi=vj
- circle(环路): 即
v
0
=
v
k
v_0 = v_k
v0=vk,起点与终点相同的路径
- simple circle: 即不包含重复节点的circle环路
- DAG(有向无环图): 有向但是不存在环路的图 , 称为有向无环图
- Hamiltonian tour(哈密尔顿环路): 每个顶点经过且只经过一次的环路, 称为哈密尔顿环路
- Eulerian tour(欧拉环路): 覆盖了所有的边,经过每一个边一次且只经过一次的环路, 称为欧拉环路
2. 如何使用代码描述图
与一般的线性结构,树型结构不同, 图由边和顶点组成, 那么计算机中如何使用代码描述图呢?
2.1 邻接矩阵和关联矩阵
描述图一般有两种方式
- 邻接矩阵
- 关联矩阵
2.1.1 邻接矩阵(adjacency matrix)
邻接矩阵就是利用矩阵元素间关系来描述顶点关系的一种方式
行为所有的顶点, 列也为所有的顶点
若
(
i
,
j
)
(i,j)
(i,j)位置的元素为1,则表示第
i
i
i个顶点为起点, 第j个顶点为终点的边
| A | B | C | D | |
|---|---|---|---|---|
| A | 1 | 1 | ||
| B | 1 | |||
| C | 1 | |||
| D |
例如上面的矩阵, 代表的图如下
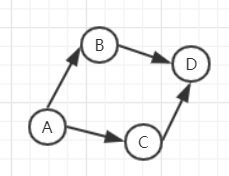
2.1.2 关联矩阵(incidence matrix)
在关联矩阵中,** 行代表顶点 , 列 代表边** , 矩阵中元素的值表明某一顶点与某一边是否有关联
注意因为一条边最多与两个节点关联, 因此如果1表示有关, 0表示无关,关联矩阵中 的列(边)最多有两个1,其他均为0
2.1.3 邻接矩阵的优点与缺点
使用邻接矩阵来描述图, 直观, 有效, 我们可以很方便的描述各种图(有向图, 网络等),他的空间复杂度为 O ( n 2 ) O(n^2) O(n2), 空间利用率极其低下 ≈ 1 n ≈\frac{1}{n} ≈n1
对于平面图(边与边不相交)而言, 实际上我们的边数都会远小于顶点数, 边数与顶点数由以下公式制约
---------------------------------1750-大数学家欧拉
3. 图类定义
3.1 顶点模板类
顶点应该至少有如下属性
- 顶点有三种状态
UNDISCOVEREDDISCOVEREDVISITED
- 入度与出度:
- 时间标签:
- 在遍历树中的父节点(int)
- 在遍历树中的优先级(最短通路, 极短跨边等)(int)
代码如下
typedef enum { UNDISCOVERED, DISCOVERED, VISITED } VStatus; //顶点状态
template <typename Tv> struct Vertex{
Tv data;
int inDegree, outDegree;
VStatus status;
int dTime, fTime;
int parent;
int priority;
Vertex(Tv const & d):
data(d), inDegree(0),outDegree(0), status(UNDISCOVERED),
dTime(-1), fTime(-1), parent(-1),
priority(INT_MAX){}
};
3.2 边模板类
边模板类应该具有如下属性
- 边的状态
UNDETERMINEDTREECROSSFORWARDBACKWARD
- 数据
- 权重
代码如下
typedef enum { UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD }EStatus; //边在遍历树中所属的类型
template <typename Te> struct Edge{
Te data;
int weiget;
EStatus status;
Edge(Te const & d, int w):
data(d), weiget(w), status(UNDETERMINED){}
};
3.3 图模板类
typedef enum { UNDISCOVERED, DISCOVERED, VISITED } VStatus; //顶点状态
typedef enum { UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD } EType; //边在遍历树中所属的类型
template <typename Tv, typename Te> //顶点类型、边类型
class Graph { //图Graph模板类
private:
void reset() { //所有顶点、边的辅助信息复位
for ( int i = 0; i < n; i++ ) { //所有顶点的
status ( i ) = UNDISCOVERED; dTime ( i ) = fTime ( i ) = -1; //状态,时间标签
parent ( i ) = -1; priority ( i ) = INT_MAX; //(在遍历树中的)父节点,优先级数
for ( int j = 0; j < n; j++ ) //所有边的
if ( exists ( i, j ) ) type ( i, j ) = UNDETERMINED; //类型
}
}
void BFS ( int, int& ); //(连通域)广度优先搜索算法
void DFS ( int, int& ); //(连通域)深度优先搜索算法
void BCC ( int, int&, Stack<int>& ); //(连通域)基于DFS的双连通分量分解算法
bool TSort ( int, int&, Stack<Tv>* ); //(连通域)基于DFS的拓扑排序算法
template <typename PU> void PFS ( int, PU ); //(连通域)优先级搜索框架
public:
// 顶点
int n; //顶点总数
virtual int insert ( Tv const& ) = 0; //插入顶点,返回编号
virtual Tv remove ( int ) = 0; //删除顶点及其关联边,返回该顶点信息
virtual Tv& vertex ( int ) = 0; //顶点v的数据(该顶点的确存在)
virtual int inDegree ( int ) = 0; //顶点v的入度(该顶点的确存在)
virtual int outDegree ( int ) = 0; //顶点v的出度(该顶点的确存在)
virtual int firstNbr ( int ) = 0; //顶点v的首个邻接顶点
virtual int nextNbr ( int, int ) = 0; //顶点v的(相对于顶点j的)下一邻接顶点
virtual VStatus& status ( int ) = 0; //顶点v的状态
virtual int& dTime ( int ) = 0; //顶点v的时间标签dTime
virtual int& fTime ( int ) = 0; //顶点v的时间标签fTime
virtual int& parent ( int ) = 0; //顶点v在遍历树中的父亲
virtual int& priority ( int ) = 0; //顶点v在遍历树中的优先级数
// 边:这里约定,无向边均统一转化为方向互逆的一对有向边,从而将无向图视作有向图的特例
int e; //边总数
virtual bool exists ( int, int ) = 0; //边(v, u)是否存在
virtual void insert ( Te const&, int, int, int ) = 0; //在顶点v和u之间插入权重为w的边e
virtual Te remove ( int, int ) = 0; //删除顶点v和u之间的边e,返回该边信息
virtual EType & type ( int, int ) = 0; //边(v, u)的类型
virtual Te& edge ( int, int ) = 0; //边(v, u)的数据(该边的确存在)
virtual int& weight ( int, int ) = 0; //边(v, u)的权重
// 算法
void bfs ( int ); //广度优先搜索算法
void dfs ( int ); //深度优先搜索算法
void bcc ( int ); //基于DFS的双连通分量分解算法
Stack<Tv>* tSort ( int ); //基于DFS的拓扑排序算法
void prim ( int ); //最小支撑树Prim算法
void dijkstra ( int ); //最短路径Dijkstra算法
template <typename PU> void pfs ( int, PU ); //优先级搜索框架
};
3.4 邻接矩阵类模板
邻接矩阵至少应该由两个集合:
- 顶点集: 由顶点集合组成
- 边集: 由邻接矩阵所表示的边, 为二维向量
template <typename Tv, typename Te>
class GraphMatrix: public Graph<Tv,Te>
{
private:
vector<Vertex<Tv>> V; //顶点集
vector< vector< Edge<Te >*> >E; // 由邻接矩阵表示的边集
public:
int n ;
int e;
GraphMatrix(){n = e = 0;}
~GraphMatrix(){
for(int j = 0; j < n; j++)
for(int k = 0 ; k< n ; k++)
delete E[j][k];
}
};
4. 图类实现
4.1 顶点操作
4.1.1 邻居枚举
邻居枚举中也利用到了哨兵的思想, 由于顶点总数为 n , 虽然在二维邻接矩阵中最大索引为n-1, 我们不妨定义n为一个哨兵, 来助于我们进行访问与遍历
template <typename Tv, typename Te>
int GraphMatrix<Tv,Te>::nextNbr(int i , int j){
while( (-1<j) && !exists(i,--j) );
return j;
}
注意虚函数要实现必须在子类中声明
4.1.2 顶点插入
顶点插入我们需要做出下面三个步骤
- 更新邻接矩阵的列数
- 更新邻接矩阵的行数
- 创建并且插入节点, 可以由下面表示的图表示

template <typename Tv, typename Te>
int GraphMatrix<Tv,Te>::insert(Tv const & j){
for(int j = 0; j <n ; j++) E[j].insert(NULL); n++;
E.insert(vector< Edge<Te>*> ( n, n ,NULL));
return V.insert(Vertex<Tv>(vertex()));
}
4.2 边操作
4.2.1 判断边是否存在
template <typename Tv, typename Te>
bool GraphMatrix<Tv, Te>::exists(int i , int j){
return (0<=i && i<n) && (0<=j && j<n) && \
E[i][j] !=NULL;
}
4.2.2 插入/删除一条边
我们需要做出如下操作
- 如果已经有边则直接返回 , 不操作
- 如果没有边, 则新建边插入, 并且更新对应顶点的出度与入度, 以及图的总数
template <typename Tv, typename Te>
void GraphMatrix<Tv, Te>::insert(Te const & edge, int w, int i ,int j){
if(exists(i,j)) return ;
E[i][j] = new Edge<Te>(edge, w);
e++;
this->V[i].outDegree++;
this->V[i].inDegree++;
}
删除只需执行相反的操作
template <typename Tv, typename Te>
Te GraphMatrix<Tv, Te>::remove(int i ,int j){
Te eBak = edge(i,j);
delete E[i][j]; E[i][j] = NULL; //删除边
e--;
this->V[i].outDegree--;
this->V[i].inDegree--;
}







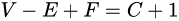














 588
588











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








